Flächeninhaltsberechnung am Kreis
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du den Flächeninhalt von Kreisen und Kreisringen berechnen kannst.
Kreisfläche
Mit Hilfe der Formel für den Umfang des Kreises U = 2 π r kannst du eine Formel für den Flächeninhalt des Kreises herleiten.
Aus den Kreisteilen lässt sich ein angenähertes Rechteck legen. Dieses Rechteck ist so breit wie der Radius des Kreises (
) und so lang wie die Hälfte des Umfangs des Kreises
.
Den Flächeninhalt eines Rechtecks bestimmst du, indem du Breite und Länge des Rechtecks miteinander multiplizierst:
.
Um
in dieser Gleichung zu ersetzen, nutzt du die Formel für den Umfang eines Kreises:
, also
.
Da das Rechteck aus den Kreisteilen zusammengesetzt ist, hat der Kreis annähernd den gleichen Flächeninhalt:
Für den
mit dem Radius
gilt:
.
Mit der Flächeninhaltsformel rechnen
Die Formel für den Flächeninhalt eines Kreises kannst du unterschiedlich nutzen.
Wenn du zu gegebenem Radius
den
möchtest, setzt du den Wert für den Radius in die Formel ein und berechnest den Flächeninhalt.
Wenn du zu gegebenem Flächeninhalt
den
möchtest, stellst du die Formel nach
um und setzt den Wert für
in die umgestellte Formel ein:

Berechne den Flächeninhalt des Kreises.
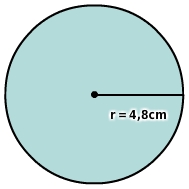 Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
 Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Flächeninhalt berechnen
Du setzt den Radius
in die Formel für die Kreisfläche ein:
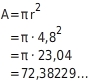 Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 72,38
Achtung:In dieser Rechnung wurde für
der
-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
für
, dann weicht dein Ergebnis etwas ab:
Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 72,38
Achtung:In dieser Rechnung wurde für
der
-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
für
, dann weicht dein Ergebnis etwas ab:

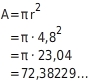 Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 72,38
Achtung:In dieser Rechnung wurde für
der
-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
für
, dann weicht dein Ergebnis etwas ab:
Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 72,38
Achtung:In dieser Rechnung wurde für
der
-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
für
, dann weicht dein Ergebnis etwas ab:

Der Kreis hat einen Flächeninhalt von etwa
.
Berechne den Radius des Kreises. Der Kreis hat einen Flächeninhalt von
.
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Radius berechnen
Du stellst die Formel für den Flächeninhalt nach r um:

 Dann setzt du 102 für
in die umgestellte Formel ein:
Führe die Division durch
und das Wurzelziehen durch, ohne zwischendurch zu runden:
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
Dann setzt du 102 für
in die umgestellte Formel ein:
Führe die Division durch
und das Wurzelziehen durch, ohne zwischendurch zu runden:
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
Der Kreis hat einen Radius von etwa
.
Kreisfläche in Sachzusammenhängen
Eine kreisförmige Fläche entsteht oft durch ein rotierendes Objekt, zum Beispiel einen Wassersprenger. Hier ist es interessant zu wissen, wie groß die Fläche ist, die bewässert wird.
Um das Volumen bestimmter Körper (zum Beispiel Zylinder und Kegel) mit kreisförmiger Grundfläche berechnen zu können, benötigst du den Flächeninhalt dieser Grundfläche. Statt des Radius ist in diesen Fällen meist der Durchmesser gegeben, da sich dieser leichter messen lässt.


Der Meistergrill
hat einen runden Grillrost mit einem Durchmesser von
cm. Ein Würstchen benötigt etwa
cm? Platz.
Wie viele Würstchen passen nebeneinander auf den Grillrost, wenn man die Fläche optimal ausnutzt?
Flächeninhalt des Grillrostes in cm" berechnen:
Der Radius (in cm) ist halb so groß wie der Durchmesser:
Du setzt den Radius
=
in die Formel für den Flächeninhalt ein:
 Das Ergebnis rundest du auf ganze Quadratzentimeter:
≈
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts
Das Ergebnis rundest du auf ganze Quadratzentimeter:
≈
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts A = 2827 cm? durch den Platzbedarf pro Würstchen 42 cm? :
≈ 67,3
Auf den Grillrost passen bis zu 67 Würstchen.
 Das Ergebnis rundest du auf ganze Quadratzentimeter:
≈
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts
Das Ergebnis rundest du auf ganze Quadratzentimeter:
≈
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts Kreisring
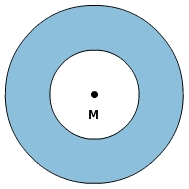
Ein Kreisring entsteht, wenn von einer Kreisfläche eine zweite kleinere Kreisfläche subtrahiert wird.
Dabei gibt es zwei Fälle:
1) Beide Kreise haben den gleichen Mittelpunkt, sie sind konzentrisch.
 2) Die Kreise haben verschiedene Mittelpunkte. Der Mittelpunkt des kleineren Kreises liegt im Inneren des größeren Kreises.
2) Die Kreise haben verschiedene Mittelpunkte. Der Mittelpunkt des kleineren Kreises liegt im Inneren des größeren Kreises.

 2) Die Kreise haben verschiedene Mittelpunkte. Der Mittelpunkt des kleineren Kreises liegt im Inneren des größeren Kreises.
2) Die Kreise haben verschiedene Mittelpunkte. Der Mittelpunkt des kleineren Kreises liegt im Inneren des größeren Kreises.

Den Flächeninhalt eines Kreisrings berechnest du, indem du den Inhalt der kleineren Kreisfläche von dem der größeren Kreisfläche subtrahierst.
Wie groß ist der Flächeninhalt des Kreisrings?
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.


Du berechnest zunächst die Flächeninhalte beider Kreise und subtrahierst dann den Inhalt der kleineren Kreisfläche von dem der größeren Kreisfläche.
Du setzt 40 für
in die Flächeninhaltsformel ein.
 Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
cm?
Du setzt 12,3 für
in die Flächeninhaltsformel ein.
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
cm?
Du setzt 12,3 für
in die Flächeninhaltsformel ein.
 Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
Du subtrahierst den Flächeninhalt des inneren Kreises vom Flächeninhalt des äußeren Kreises.
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
Du subtrahierst den Flächeninhalt des inneren Kreises vom Flächeninhalt des äußeren Kreises.
 Der Flächeninhalt dieses Kreisrings beträgt etwa
cm?.
Der Flächeninhalt dieses Kreisrings beträgt etwa
cm?.
 Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
cm?
Du setzt 12,3 für
in die Flächeninhaltsformel ein.
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
cm?
Du setzt 12,3 für
in die Flächeninhaltsformel ein.
 Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
Du subtrahierst den Flächeninhalt des inneren Kreises vom Flächeninhalt des äußeren Kreises.
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈
Du subtrahierst den Flächeninhalt des inneren Kreises vom Flächeninhalt des äußeren Kreises.
 Der Flächeninhalt dieses Kreisrings beträgt etwa
cm?.
Der Flächeninhalt dieses Kreisrings beträgt etwa
cm?.
Du kannst Zeit einsparen, wenn du den Flächeninhalt des Kreisrings in einem Schritt berechnest.
Der Flächeninhalt des Kreisrings ist die Differenz aus der Fläche des äußeren Kreises und der Fläche des inneren Kreises.
Jetzt setzt du die Flächeninhaltsformel zweimal in die Gleichung ein:
Durch Ausklammern von
erhältst du:
Jetzt setzt du die beiden Werte für die Radien in die Gleichung ein und berechnest
in cm?:
 Das Ergebnis rundest du dann auf die gewünschte Genauigkeit, z.B. auf mm" genau, also auf 2 Stellen nach dem Komma:
≈
cm?
Das Ergebnis rundest du dann auf die gewünschte Genauigkeit, z.B. auf mm" genau, also auf 2 Stellen nach dem Komma:
≈
cm?
 Das Ergebnis rundest du dann auf die gewünschte Genauigkeit, z.B. auf mm" genau, also auf 2 Stellen nach dem Komma:
≈
cm?
Das Ergebnis rundest du dann auf die gewünschte Genauigkeit, z.B. auf mm" genau, also auf 2 Stellen nach dem Komma:
≈
cm?

