Flächen- und Umfangsberechnung von Figuren
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du den Umfang und den Flächeninhalt eines Dreiecks, eines Trapezes oder eines Drachens berechnen kannst.
Höhen im Dreieck
In einem Dreieck gibt es drei Höhen. Eine Höhe gehört zu einem Eckpunkt und der gegenüberliegenden Seite, die dann Grundseite genannt wird. Die Länge der Höhe ist der Abstand des Eckpunkts von der Grundseite. Der Abstand selbst wird auch als Höhe bezeichnet.Die Höhen eines Dreiecks können innerhalb, aber auch außerhalb des Dreiecks liegen.
Die Höhe über der Seite a Die drei Höhen des Dreiecks ABC
Die drei Höhen des Dreiecks ABC
 Die drei Höhen des Dreiecks ABC
Die drei Höhen des Dreiecks ABC
Höhen in einem Dreieck einzeichnen
Höhen im Dreieck einzeichnen
So zeichnest du die Höhen in einem Dreieck ein:


Höhen außerhalb des Dreiecks
Beim stumpfwinkligen Dreieck liegen zwei der drei Höhen außerhalb des Dreiecks.

Höhen in einem rechtwinkligen Dreieck
Beim rechtwinkligen Dreieck stimmen zwei der drei Höhen mit Seiten des Dreiecks überein.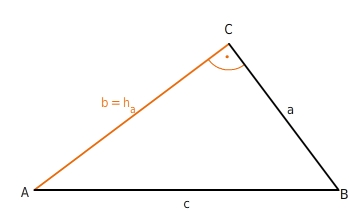

Die Höhe über der Seite a stimmt mit der Seite b überein.
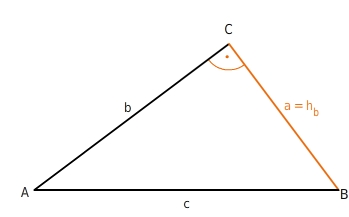
Die Höhe über der Seite b stimmt mit der Seite a überein.
Höhe und Mittelparallele im Trapez
Die Höhe eines Trapezes ist der Abstand der beiden zueinander parallelen Seiten, also die Länge einer Strecke zwischen den beiden Seiten, die senkrecht auf diesen (oder deren Verlängerungen) steht. Die Strecke kann also innerhalb oder außerhalb des Trapezes liegen. Sie wird ebenfalls Höhe genannt.Wenn die beiden parallelen Trapezseiten durch einen senkrechten Schenkel verbunden sind, ist die Höhe gleich diesem Schenkel.Die Mittelparallele im Trapez ist die Parallele zur Grundseite durch die Mittelpunkte der beiden Schenkel und wird deshalb auch als Mittellinie bezeichnet.
Die Höhe eines Trapezes Die Mittelparallele eines Trapezes
Die Mittelparallele eines Trapezes
 Die Mittelparallele eines Trapezes
Die Mittelparallele eines Trapezes
Höhen außerhalb des Trapezes
Eine Höhe im Trapez kann an verschiedenen Stellen eingezeichnet werden und muss nicht in einem Eckpunkt beginnen oder enden. Sie kann auch außerhalb des Trapezes liegen.

Höhe in einem Trapez einzeichnen

Höhe im Trapez einzeichnen
Du zeichnest die Höhe in das Trapez ein, indem du eine zu den parallelen Seiten rechtwinklige Strecke konstruierst.

Mittelparallele in einem Trapez einzeichnen

Mittelparallele im Trapez einzeichnen
Du zeichnest die Mittelparallele in das Trapez ein, indem du eine Strecke zeichnest, die durch die Mittelpunkte der beiden Schenkel verläuft und parallel zur Grundseite ist.

Umfang eines Dreiecks
Den Umfang eines Dreiecks (U) berechnest du, indem du die drei Seitenlängen des Dreiecks addierst.


Umfang eines Dreiecks:
Umfang eines Dreiecks berechnen
Berechne den Umfang U des Dreiecks.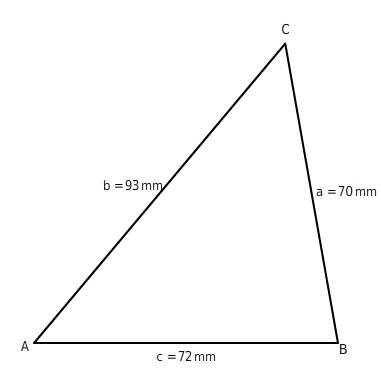

Umfang berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Umfang des Dreiecks: Der Umfang beträgt
.
Der Umfang beträgt
.
Umfang eines gleichschenkligen Dreiecks berechnen
Berechne den Umfang U des Dreiecks.

Umfang berechnen
Da die Seiten b und c gleich lang sind (b = c), kannst du die Formel zur Umfangsberechnung nur mit den Längen a und b ausdrücken: Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Umfang des Dreiecks.
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Umfang des Dreiecks.
Umfang eines Trapezes
Du berechnest des Umfang des Trapezes (U), indem du die Länge aller Seiten addierst:


Umfang eines Trapezes:
Umfang eines Trapezes berechnen
Berechne den Umfang des Trapezes.

Umfang berechnen
Die Seitenlängen des Trapezes haben dieselbe Einheit, also kannst du den Umfang direkt berechnen. 

Umfang eines gleichschenkligen Trapezes berechnen
Drücke die Formel zur Umfangsberechnung eines gleichschenkligen Trapezes mit Hilfe von a, b und c aus.

Formel finden
Da die Seiten b und d gleich lang sind, kannst du die Formel zur Umfangsberechnung nur mit den Längen a, b und c ausdrücken: 

Berechne den Umfang des gleichschenkligen Trapezes. 

Umfang berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Umfang des Trapezes: 

Umfang eines Drachens
Beim Drachen gibt es zwei Paare benachbarter gleich langer Seiten. Deshalb kannst du zur Berechnung des Umfangs eines Drachens (U) die folgende Formel benutzen: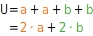


Umfang eines Drachens:
Berechne den Umfang des Drachens.

Umwandeln
Die Seitenlängen sind in unterschiedlichen Längeneinheiten gegeben. Damit du den Umfang berechnen kannst, müssen alle Angaben in eine gemeinsame Einheit umgewandelt werden.
=
Umfang berechnen
Du setzt die Werte in die Formel ein und erhältst so den Umfang: 

Flächeninhalt eines Dreiecks
Den Flächeninhalt eines Dreiecks (A) berechnest du, indem du die Länge der Grundseite g mit der zugehörigen Höhe h multiplizierst und das Produkt durch 2 dividierst:
Da es drei verschiedene Grundseiten und die jeweiligen zugehörigen Höhen im Dreieck gibt, gibt es drei verschiedene Möglichkeiten den Flächeninhalt zu berechnen:Mit der Grundseite a:
, wobei a die Länge der Seite a und
die zugehörige Höhe bezeichnet.Mit der Grundseite b:
, wobei b die Länge der Seite b und
die zugehörige Höhe bezeichnet.Mit der Grundseite c:
, wobei c die Länge der Seite c und
die zugehörige Höhe bezeichnet.
Den Flächeninhalt eines rechtwinkligen Dreiecks (A) berechnest du, indem du die Längen der Seiten, die den rechten Winkel einschließen, multiplizierst:
, wobei a und b die Längen der Seiten, die den rechten Winkel einschließen, bezeichnen.
Flächeninhalt eines Dreiecks:
Flächeninhalt eines rechtwinkligen Dreieck:
Woher kommt die Formel zur Flächeninhaltsberechnung eines Dreiecks?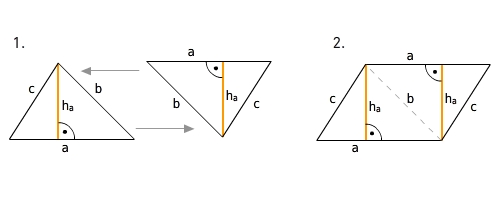

Wenn du zwei identische Dreiecke wie im Bild anlegst, erhältst du ein Parallelogramm. Daher ist der Flächeninhalt eines Dreiecks gleich der Hälfte des Flächeninhalts des erhaltenen Parallelogramms.
Woher kommt die Formel zur Flächeninhaltsberechnung eines rechtwinkligen Dreiecks?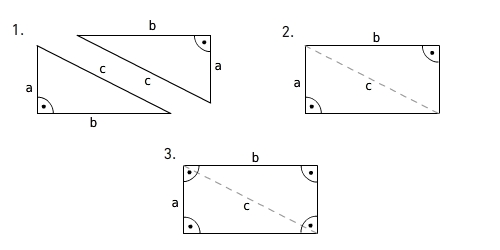

Wenn du zwei identische rechtwinklige Dreiecke wie im Bild anlegst, erhältst du ein Rechteck mit Länge a und Breite b. Daher ist der Flächeninhalt eines rechtwinkligen Dreiecks gleich der Hälfte des Flächeninhalts des Rechtecks.
Flächeninhalt eines Dreiecks
Berechne den Flächeninhalt des Dreiecks.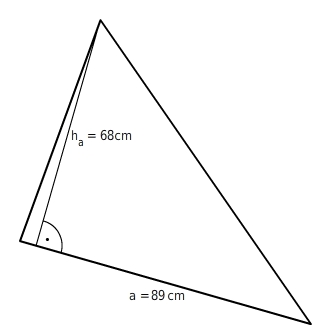

Flächeninhalt berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Flächeninhalt des Dreiecks: 

Flächeninhalt eines rechtwinkligen Dreiecks
Berechne den Flächeninhalt des Dreiecks.

Flächeninhalt berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Flächeninhalt des Dreiecks:  Der Flächeninhalt beträgt
.
Der Flächeninhalt beträgt
.
 Der Flächeninhalt beträgt
.
Der Flächeninhalt beträgt
.
Flächeninhalt eines Trapezes
Du kannst den Flächeninhalt eines Trapezes (A) anhand der parallelen Seiten und der Höhe bestimmen, indem du die Summe der Länge der parallelen Seiten mit der Höhe multiplizierst und dieses Produkt durch 2 dividierst:
Den Flächeninhalt eines Trapezes (A) kannst du auch mit Hilfe der Länge der Mittelparallelen und der Höhe berechnen.
Woher kommt die Formel anhand der parallelen Seiten den Flächeninhalt eines Trapezes zu berechnen?

Wenn du zwei identische Trapeze wie im Bild anlegst, erhältst du ein Parallelogramm mit Grundseite a+c und Höhe h. Daher ist der Flächeninhalt eines Trapezes gleich der Hälfte des Flächeninhalts des erhaltenen Parallelogramms.
Woher kommt die Formel anhand der Mittelparallelen den Flächeninhalt eines Trapezes zu berechnen?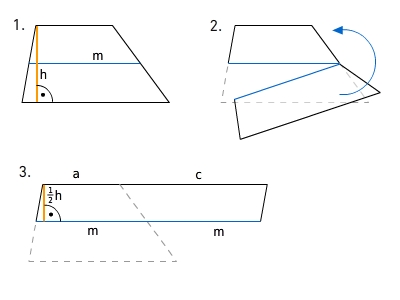

Ein Trapez kannst du entlang der Mittelparallele trennen und in ein Parallelogramm mit Grundseite
und Höhe
umwandeln. Daraus erhältst du die folgende Formel zur Flächeninhaltsberechnung:
Flächeninhalt eines Trapezes:
und
Es gibt zwei Wege den Flächeninhalt eines Trapezes zu berechnen.

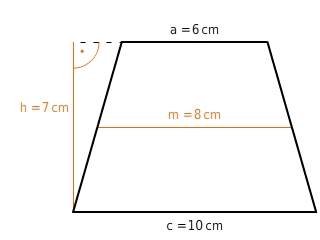

 Der Flächeninhalt des Trapezes beträgt 56
. Der Flächeninhalt des Trapezes beträgt 56
.
Der Flächeninhalt des Trapezes beträgt 56
. Der Flächeninhalt des Trapezes beträgt 56
.



 Der Flächeninhalt des Trapezes beträgt 56
. Der Flächeninhalt des Trapezes beträgt 56
.
Der Flächeninhalt des Trapezes beträgt 56
. Der Flächeninhalt des Trapezes beträgt 56
.
Flächeninhalt eines Drachens
Den Flächeninhalt eines Drachens berechnest du, indem du die Länge der Diagonalen multiplizierst und das Produkt durch 2 dividierst.
, wobei e und f die Diagonalenlängen des Drachens bezeichnen.
Woher kommt die Formel zur Flächeninhaltsberechnung eines Drachens?

Ein Drachen mit den Diagonalen e und f kannst du zerlegen und in ein Rechteck mit der Länge f und der Breite
umwandeln. Daraus erhältst du die folgende Formel zur Flächeninhaltsberechnung eines Drachens:
Flächeninhalt eines Drachens:
Berechne den Flächeninhalt des Drachens 

Flächeninhalt berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Flächeninhalt des Drachens: Der Flächeninhalt beträgt
.
Der Flächeninhalt beträgt
.
 Der Flächeninhalt beträgt
.
Der Flächeninhalt beträgt
.
Berechne den Flächeninhalt des Drachens 

Umwandeln
Hier sind die Seitenlängen in unterschiedlichen Längeneinheiten gegeben. Damit du den Umfang berechnen kannst, müssen alle Angaben in eine gemeinsame Einheit umgewandelt werden.
Flächeninhalt berechnen
Du setzt die Werte in die Formel ein und erhältst so den Flächeninhalt des Drachens: Der Flächeninhalt beträgt
.
Der Flächeninhalt beträgt
.
 Der Flächeninhalt beträgt
.
Der Flächeninhalt beträgt
.

