Exponentielles Wachstum
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenBerechnen des Wachstumsfaktors aus einer Angabe in Prozent
Aus einer Prozentangabe kannst du den Wachstumsfaktor b bestimmen:
Eine Zunahme
entspricht einem Wachstumsfaktor
Wächst eine Bakterienpopulation von anfangs 200 Bakterien stündlich um
, dann sind es nach einer Stunde 250 Bakterien.
Wächst eine Bakterienpopulation von anfangs 200 Bakterien stündlich um
, dann sind es nach einer Stunde 250 Bakterien.
Eine Abnahme
entspricht einem Wachstumsfaktor
Eine Maschine mit einem Neuwert von
hat bei einem jährlichen Wertverlust von
nach einem Jahr einen Wert von
.
Eine Maschine mit einem Neuwert von
hat bei einem jährlichen Wertverlust von
nach einem Jahr einen Wert von
.
Berechnungen zum exponentiellen Wachstum
Willst du die Werte einer exponentiell zu- oder abnehmenden Größe über mehrere Schritte hinweg berechnen, verwendest du
des
.
Hat die Größe den Anfangswert
, dann gilt für den Wert
(nach
Schritten):
Die Zahl der in einer Petrischale kultivierten Zellen verdoppelt sich stündlich.Bei einem Anfangswert von 46 Zellen befinden sich nach 3 Stunden 368 Zellen und nach 5 Stunden
Zellen in der Schale.
Verdopplung pro Schritt 
Umgekehrt kannst du den Anfangswert
berechnen oder den Wachstumsfaktor b:
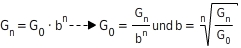
Berechnungen mit Anteilen von Wachstumsschritten
In der Gleichung
bestimmt die Anzahl n der Wachstumsschritte den
des Wachstumsfaktors.
Auch zur Berechnung von Werten zwischen zwei
Schritten kannst du
des Wachstumsfaktors verwenden.Der Exponent ist dann der Anteil am ganzen Schritt.
Na-24 hat eine
von ca. 15 Stunden. Eine Materialprobe enthält zu Beginn einer Versuchsreihe
des Natrium-Isotops Na-24.
Bestand nach k Stunden:
