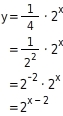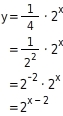Eigenschaften von Exponentialfunktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenEigenschaften der Exponentialfunktion
Der Graph einer Exponentialfunktion
mit
,
≠
enthält die Punkte 0 | 1 und 1 | b .
Du kannst also den Funktionsterm einer Exponentialfunktion schnell mit Hilfe des Graphen bestimmen.
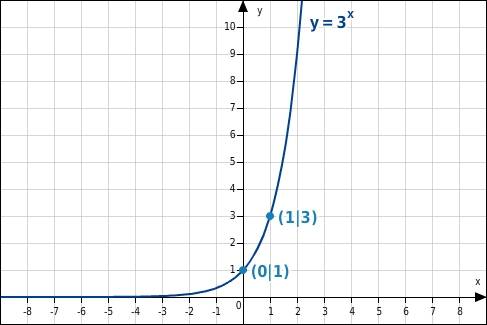 Der Graph enthält die Punkte
Der Graph enthält die Punkte
Der Definitionsbereich
einer Exponentialfunktion ist ℝ, der
ist 0 ; ∞ . Exponentialfunktionen haben also keine
.
Die Funktionswerte nähern sich aber beliebig dicht der Null an. Die x-Achse bzw. die Gerade
ist die waagerechte
der Exponentialfunktion.
Exponentialfunktionen mit
sind monoton steigend.Exponentialfunktionen mit
sind monoton fallend.
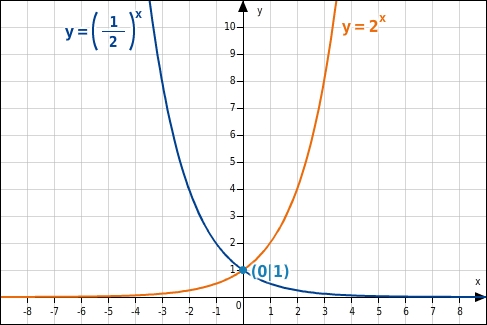
Die Graphen der Exponentialfunktionen
und
sind zueinander symmetrisch bezüglich der y-Achse.
mit
und
mit

Die allgemeine Exponentialfunktion
Du kennst die normale Exponentialfunktion mit
.
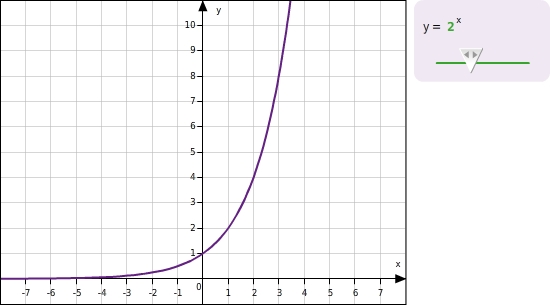 Durch die Verwendung von
kannst du die Gleichung verändern, um z.B. verschiedene exponentielle Wachstumsvorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
Der Parameter
wird auch Streckfaktor genannt, denn die
der normalen Exponentialfunktion
wird gestreckt
Durch die Verwendung von
kannst du die Gleichung verändern, um z.B. verschiedene exponentielle Wachstumsvorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
Der Parameter
wird auch Streckfaktor genannt, denn die
der normalen Exponentialfunktion
wird gestreckt a > 1 oder gestaucht 0 < a < 1 .
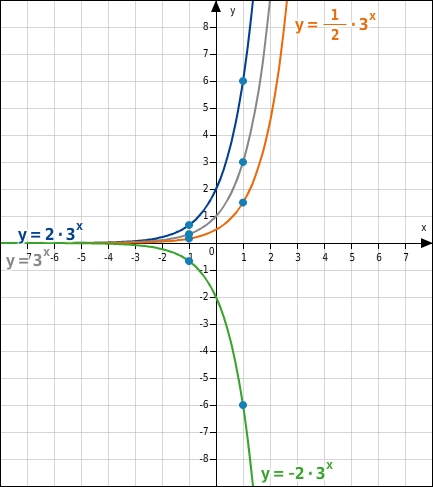
Ist
negativ, wird die Kurve zusätzlich an der x-Achse gespiegelt.Die Graphen der
enthalten die Punkte 0 | a und 1 | b · a .
Für
ist der
, für
ist
.
Die Graphen haben also keine
.
Die Funktionswerte nähern sich aber beliebig dicht der Null an. Die x-Achse bzw. die Gerade
ist die waagerechte
der Exponentialfunktion.
 Durch die Verwendung von
kannst du die Gleichung verändern, um z.B. verschiedene exponentielle Wachstumsvorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
Der Parameter
wird auch Streckfaktor genannt, denn die
der normalen Exponentialfunktion
wird gestreckt
Durch die Verwendung von
kannst du die Gleichung verändern, um z.B. verschiedene exponentielle Wachstumsvorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
Der Parameter
wird auch Streckfaktor genannt, denn die
der normalen Exponentialfunktion
wird gestreckt
mit
mit
mit

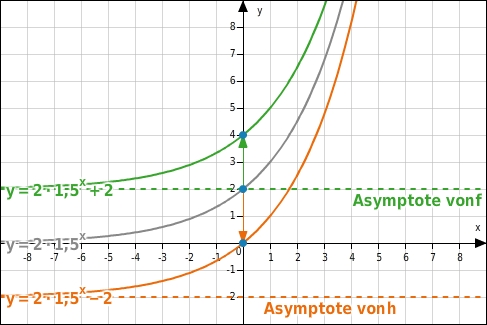
Verschiebung in y-Richtung
In der Funktionsgleichung
bewirkt der Parameter
eine Verschiebung des Funktionsgraphen der
in y-Richtung.
Für
erfolgt die Verschiebung nach oben, für
nach unten.
Durch die Verschiebung ändert sich im Fall
der Wertebereich
zu d ; ∞ .
Die Asymptote wird verschoben nach
.
Durch die Verschiebung nach unten kommt eine Nullstelle hinzu.
mit
mit
mit

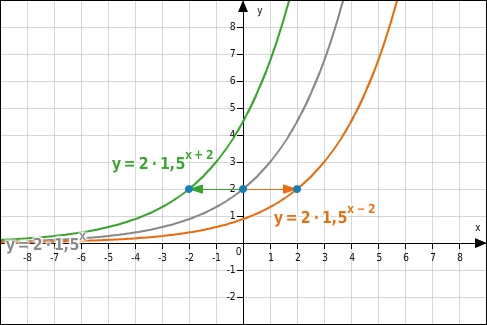
Verschiebung in x-Richtung
In der Funktionsgleichung
bewirkt der Parameter
eine Verschiebung der
in x-Richtung.
Für
erfolgt die Verschiebung nach links, für
nach rechts.
Durch die Verschiebung ändert sich der Wertebereich
nicht.
mit
mit
mit

Funktionen der Form
sind auch
, denn eine Verschiebung in x-Richtung kann auch als Streckung oder Stauchung beschrieben werden.
Für
mit
entspricht die Verschiebung um
Einheiten nach links einer Streckung mit dem Faktor
, denn
.
Die Verschiebung um
Einheiten nach rechts entspricht einer Stauchung mit dem Faktor
, denn
.
Die Verschiebung der Exponentialkurve
um 3 Einheiten nach links entspricht einer Streckung mit dem Faktor 8.
Mit Hilfe von
erhältst du
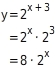
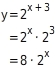
Die Stauchung der Exponentialkurve
mit dem Faktor
entspricht einer Verschiebung um zwei Einheiten nach rechts.
Mit Hilfe von
erhältst du