Diagramme erstellen und auswerten
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn dieser Erklärung erfährst du, wie du Daten in Diagrammen abbilden kannst, wie du im Diagramm abliest und wie du eines erstellst. Außerdem werden dir verschiedene Diagrammtypen sowie ihre Vor- und Nachteile vorgestellt.
Verwendung von Diagrammen
Um verschiedene Daten übersichtlicher als in einem Text oder in einer Tabelle darstellen zu können, kannst du diese in Diagrammen veranschaulichen. Anhand der Diagramme kannst du beispielsweise einen bestimmten Verlauf von Daten erkennen, Größen miteinander vergleichen, einen Trend ablesen und Daten interpretieren.Es gibt unterschiedliche Formen von Diagrammen. Je nachdem welche Daten vorliegen, wird ein für die Daten geeignetes Diagramm zur grafischen Darstellung gewählt.
Diagramm aus einer Strichliste erstellen Die Schulcafeteria möchte von Schülern einer fünften Klasse wissen, welche Snacks in der Pause verkauft werden sollen. Die Antworten werden in einer Strichliste festgehalten. Marie erstellt zu der Strichliste ein Diagramm. 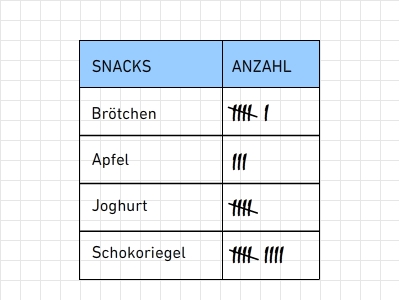
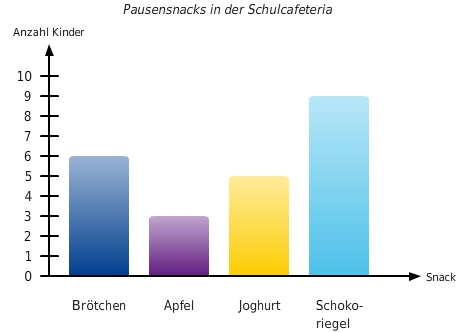


Im Diagramm sind die vorliegenden Daten übersichtlicher und leichter erfassbar dargestellt, als in der Strichliste. So ist es einfacher die Daten zum Beispiel anhand der Höhe der Säulen miteinander zu vergleichen.
Diagramm aus einer Tabelle erstellen Anna pflanzt einen Sonnenblumenkern in einen Topf und gießt ihn täglich. Sobald die Sonnenblume zum Vorschein kommt, misst Anna die Pflanze jeden Abend, um das Wachstum der Sonnenblume zu untersuchen. 
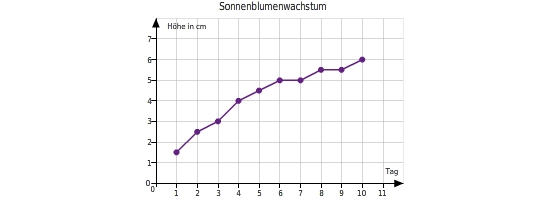


Im Diagramm sind die vorliegenden Daten übersichtlicher und leichter erfassbar dargestellt, als in der Tabelle. Du kannst so auf einen Blick einen Trend der Daten erkennen. Sonnenblumen werden in der Regel bis zu hoch. Das Diagramm zeigt dir, dass die Sonnenblume auch nach dem zehnten Tag wahrscheinlich weiter wachsen wird.
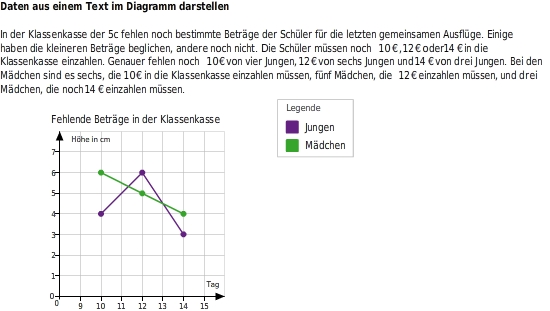
Wenn dir Daten in der Form eines Textes vorliegen, dann ist es schwierig sie miteinander zu vergleichen. Diagramme sind in dieser Hinsicht übersichtlicher und einfacher zu verstehen. Bei diesem Diagramm kannst du den noch fehlenden Betrag der Jungen und Mädchen in der Klassenkasse direkt miteinander vergleichen.
Kurvendiagramm
Zum Einzeichnen von Daten in ein Kurvendiagramm benötigst du die x- und die y-Achse. Die waagerecht verlaufende Linie wird in der Regel x-Achse genannt und die dazu senkrecht verlaufende Linie heißt dann y-Achse. Die senkrecht aufeinander stehenden Achsen bilden das so genannte rechtwinklige (orthogonale) Koordinatenkreuz.Ein Kurvendiagramm benutzt du, wenn du einen zeitlichen Verlauf oder einen Trend verdeutlichen möchtest. Außerdem kannst du in einem Kurvendiagramm die Unterschiede oder auch ähnlichkeiten der Daten gut erkennen. Du solltest allerdings wegen der übersichtlichkeit nicht zu viele Datenreihen zugleich darstellen.
x- und y-Achse im Kurvendiagramm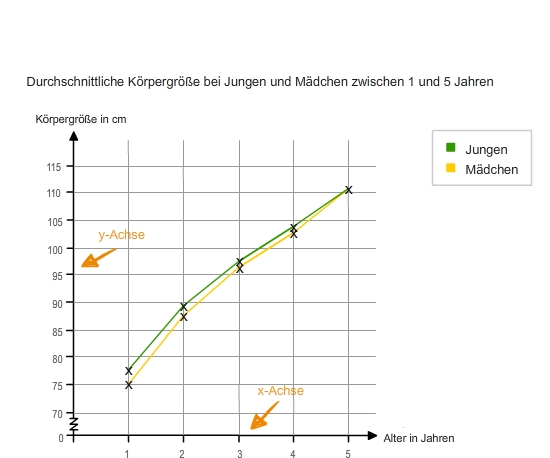

Die x- und y-Achse werden bei Diagrammen mit einer Achsenbeschriftung versehen. Diese Beschriftung beschreibt, was an der jeweiligen Achse dargestellt wird. Bei zeitlichen Verläufen wird die Zeit (zum Beispiel Stunden/Monate/Jahre) meistens an der x-Achse dargestellt.Anhand eines Kurvendiagramms kannst du einen Trend ablesen: Der Trend dieser Kurven geht nach oben. Es ist also zu vermuten, dass die Jungen und Mädchen auch in den folgenden Jahren an Körpergröße gewinnen werden.
Ein Kurvendiagramm erstellen
Ablesen im Kurvendiagramm Kaum ist der erste Schnee gefallen baut Daniel einen Schneemann. Eine Woche später steigt die Lufttemperatur auf knapp über . Daraufhin beobachtet Daniel jeden Morgen wie sein Schneemann schmilzt und nach fünf Tagen ganz verschwindet. 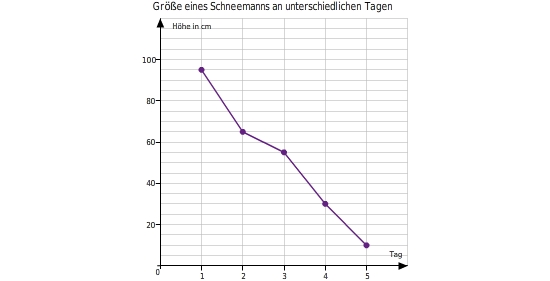

Lies am Diagramm ab: Wie hoch ist der Schneemann am zweiten Tag?
Du liest an der y-Achse ab, wie hoch der Schneemann am zweiten Tag ist.
Der Schneemann ist am zweiten Tag hoch. 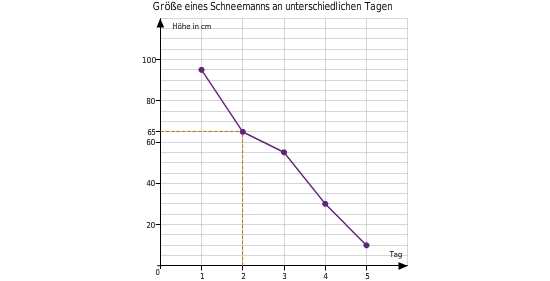

An welchem Tag ist der Schneemann hoch?
Du liest an der x-Achse ab, an welchem Tag der Schneemann hoch ist.
Der Schneemann ist am vierten Tag hoch. 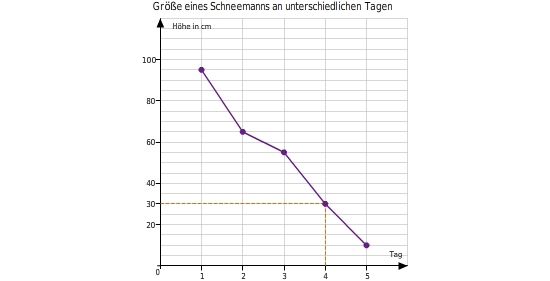

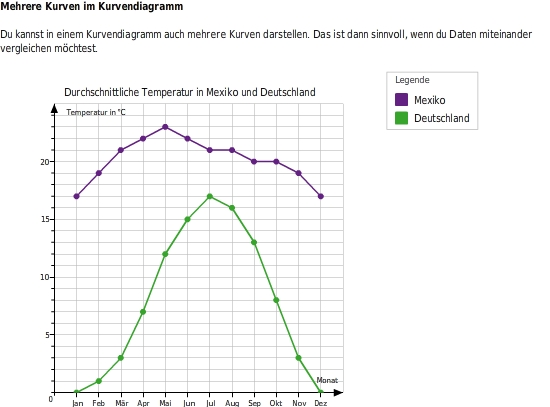
Bei diesem Kurvendiagramm zum Vergleich der Durchschnittstemperaturen in zwei Ländern ist auf einen Blick sichtbar, dass die Durchschnittstemperatur in Mexiko immer über der Durchschnittstemperatur in Deutschland liegt.
Säulen- und Balkendiagramm
Zum Einzeichnen von Daten in ein Säulendiagramm oder ein Balkendiagramm benötigst du die x- und die y-Achse. Die waagerecht verlaufende Linie wird in der Regel x-Achse genannt und die dazu senkrecht verlaufende Linie heißt dann y-Achse. Die senkrecht aufeinander stehenden Achsen bilden das so genannte rechtwinklige (orthogonale) Koordinatenkreuz.Anschließend werden unterschiedliche Zahlenwerte oder Größenverhältnisse durch unterschiedliche Höhen der Säulen (beziehungsweise Längen der Balken im Balkendiagramm) veranschaulicht. Mit einem Säulendiagramm und einem Balkendiagramm kannst du Häufigkeitsdaten und Vergleiche gut abbilden. Mit diesem Diagrammtyp kannst du Unterschiede oder auch ähnlichkeiten veranschaulichen. In der Regel werden in einem Säulendiagramm Zahlenwerte wie zum Beispiel Daten zu verschiedenen Zeiten, Schulnoten, Monate … in einer bestimmten Reihenfolge dargestellt. Das Balkendiagramm dagegen wählst du, wenn die Daten nicht angeordnet werden können, zum Beispiel bei Farben, Namen, Berufen, ... .
Im Säulendiagramm ablesen In der ersten Woche nach dem Kinostart eines beliebten Kinderfilms, wurden die Besucherzahlen im Star-Kino gezählt. Insgesamt wurden Besucher gezählt. 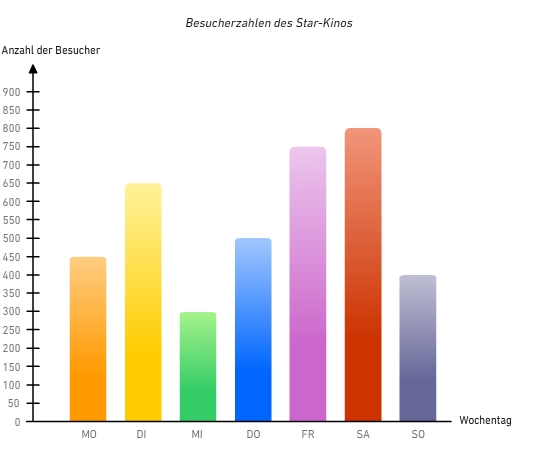

Lies am Diagramm ab: Wie viele Kinobesucher waren am Donnerstag im Star-Kino?
Du liest an der y-Achse ab, wie viele Kinobesucher an einem Donnerstag im Star-Kino waren.
Am Donnerstag waren 500 Besucher im Star-Kino. 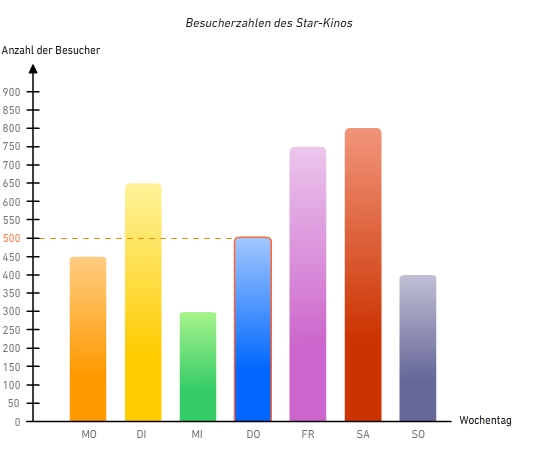

An welchem Wochentag waren genau 800 Kinobesucher im Star-Kino?
Du liest an der x-Achse ab, an welchem Wochentag genau 800 Kinobesucher im Star-Kino waren.
Am Samstag waren 800 Kinobesucher im Star-Kino. 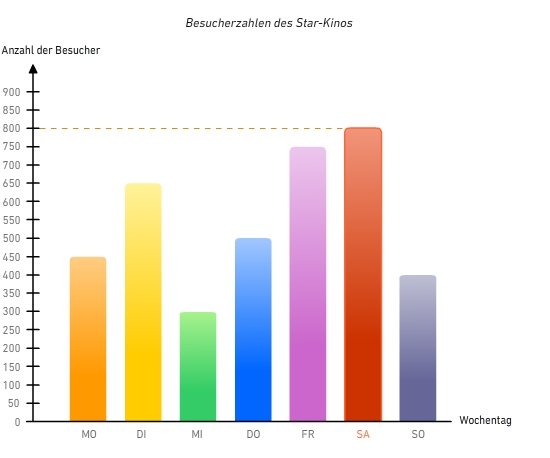

Im Balkendiagramm ablesen Jonas und Lena haben einige Mitschüler nach ihrer Lieblingsfarbe befragt. Die Antworten haben sie in einem Balkendiagramm abgebildet. 

Lies am Diagramm ab: Wie viele Kinder geben die Farbe grün als Lieblingsfarbe an?
Du liest an der x-Achse ab, wie viele Kinder die Farbe grün als ihre Lieblingsfarbe angeben.
Genau 40 Kinder geben die Farbe grün als ihre Lieblingsfarbe an. 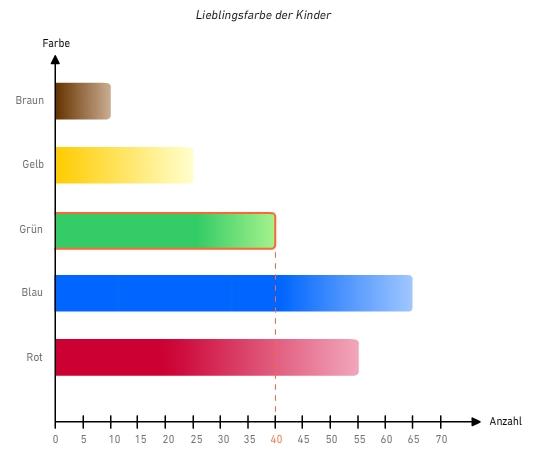

Genau 55 Kinder haben die gleiche Lieblingsfarbe. Welche Farbe ist das?
Du liest an der y-Achse ab, welche Farbe die Lieblingsfarbe von genau 55 Kindern ist.
Rot ist die Lieblingsfarbe von 55 Kindern. 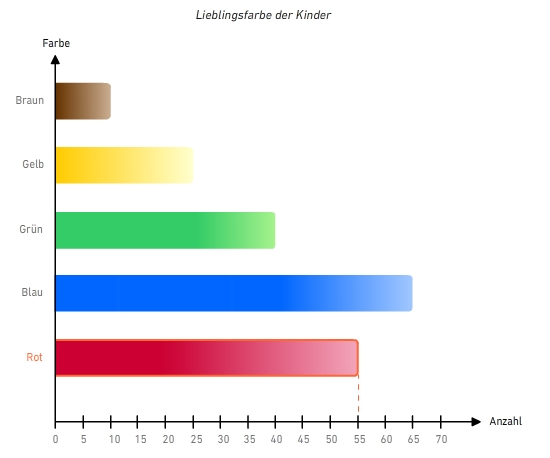

Gruppierte Säulen im Säulendiagramm Um Daten miteinander zu vergleichen, kannst du auch mehrere Kategorien in einem Säulendiagramm abbilden. 140 Jungen und 135 Mädchen sollten in einer Befragung angeben, was ihnen in ihrer Freizeit wichtig ist. Die Ergebnisse werden in einem Säulendiagramm abgebildet. 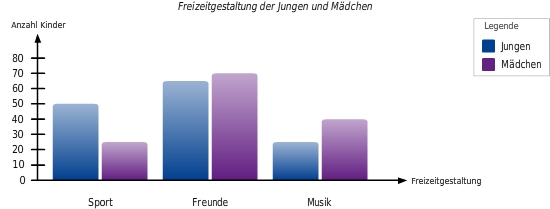

Bei diesem Säulendiagramm zum Vergleich der Freizeitgestaltung von Jungen und Mädchen ist auf einen Blick sichtbar, dass sowohl Jungen als auch Mädchen ihre freie Zeit gern mit Freunden verbringen.
Weitere Diagrammtypen
Es gibt noch viele weitere Diagrammtypen und grafischen Darstellungen, wie beispielsweise Kreisdiagramme, Streifendiagramme, Bilddiagramme oder auch Diagramme, die mehrere Diagrammtypen in einem darstellen.
Kreisdiagramm Mit einem Kreisdiagramm kannst du Mengen abbilden und Gegensätze verdeutlichen. In einem Kreisdiagramm werden die beobachteten Daten als Bruchteile von einem Ganzen dargestellt. 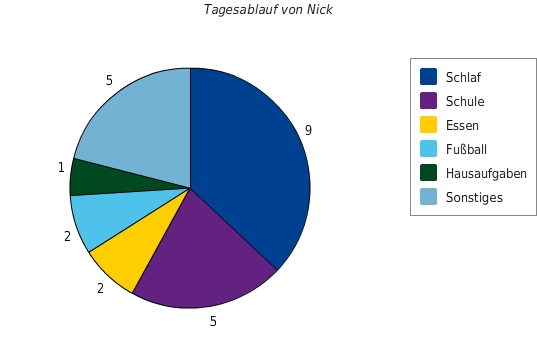

In dem Kreisdiagramm ist dargestellt, wie viele Stunden Nick durchschnittlich für seine Tagesaktivitäten benötigt.
Streifendiagramm Wenn du einen Anteil am Ganzen darstellen möchtest, dann eignet sich dafür ein Streifendiagramm. Das Streifendiagramm ist also eine ähnliche Darstellung wie das Kreisdiagramm. 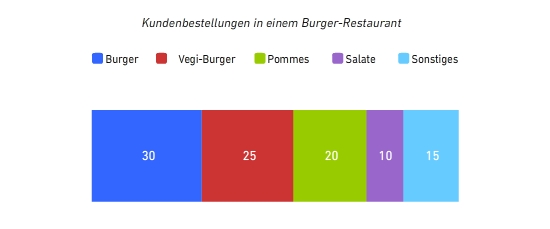

Der Besitzer eines Burger-Restaurants untersucht, welche Gerichte seine Kunden über das Jahr verteilt am häufigsten bestellt haben. Im Streifendiagramm ist zu erkennen, dass die Kunden am liebsten Burger essen.
Bilddiagramm Manchmal gibt es geeignete Symbole, um die Größe einer Zahl zu veranschaulichen. 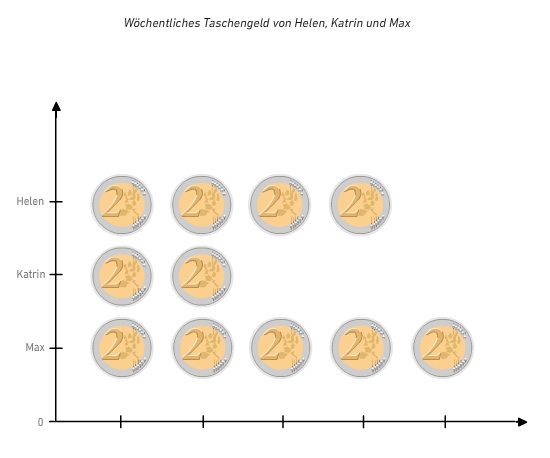

In diesem Bilddiagramm wurden Geldbeträge durch eine bestimmte Anzahl von Münzen veranschaulicht.
Mehrere Diagrammtypen in einem Diagramm Du kannst auch verschiedene Diagrammtypen in einem Diagramm abbilden, um Daten besser miteinander zu vergleichen oder wenn zwei Themen in einem Diagramm gegenübergestellt werden sollen. Solche Diagrammtypen besitzen zwei verschiedene Größenachsen, eine links und eine rechts. In einer Stadt im Ruhrgebiet wurden die durchschnittliche Temperatur in "C sowie der durchschnittliche Niederschlag in mm für das ganze Jahr 2000 erfasst. Die Daten wurden in einem gemischten Diagramm mit den Temperaturwerten als Punkte einer Kurve und den Niederschlagswerten als Säulen dargestellt. 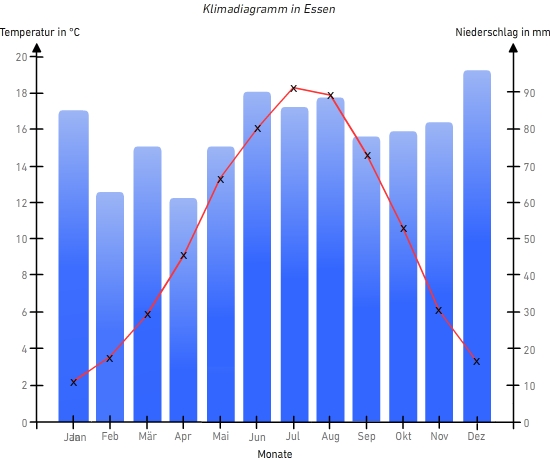

In diesem Diagramm werden zwei Themen gegenübergestellt: der durchschnittliche Temperaturverlauf und der durchschnittliche Niederschlag einer Stadt im Ruhrgebiet. Das Klimadiagramm als Kombination aus zwei Diagrammtypen bietet einen schnellen und groben überblick über die Witterungsverhältnisse an einem Ort.
Median und Mittelwert
Den Median (auch Zentralwert genannt) bestimmst du, indem du die Zahlwerte der Größe nach sortierst. Der Median entspricht dann dem Wert, der sich genau in der Mitte befindet. Den Mittelwert berechnest du, indem du alle Beobachtungswerte addierst und diese dann durch die Gesamtanzahl der Beobachtungen dividierst. Den Median verwendest du, wenn du die Daten in eine sinnvolle Reihenfolge bringen kannst, aber der Abstand zwischen den einzelnen Werten ungleich oder nicht bestimmbar ist. Außerdem eignet sich der Median besser als der Mittelwert zur Beschreibung von Daten, bei denen es extrem kleine oder extrem große Werte gibt. Im Gegensatz zum Mittelwert verändert sich der Median durch einzelne Ausreißer kaum.
Median bei ungerader Anzahl Bei einer ungeraden Anzahl kannst du den Median direkt ablesen. Es ist der Wert, der nach dem Sortieren in der Mitte steht. Familie Schmidt hat fünf Kinder, die unterschiedlich groß sind. Der Vater misst in Zentimetern die Körpergröße all seiner Kinder, um den Median zu bestimmen.  Bestimme den Median.
Bestimme den Median. 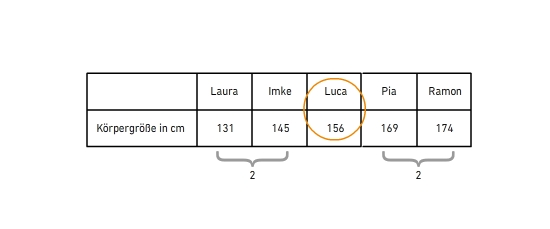
Sortieren
Als erstes musst du die Werte der Größe nach sortieren. Nach dem Sortieren: 
Median bestimmen
Familie Schmidt hat fünf Kinder, das ist eine ungerade Anzahl - du kannst also den Median direkt ablesen. Der Median entspricht dem Wert, der sich genau in der Mitte befindet: .

Median bei gerader Anzahl Bei einer geraden Anzahl von Werten, bestimmst du den Median, indem du die Summe der beiden mittleren Werte bildest und durch 2 dividierst. Familie Kleinschmidt hat vier Kinder, zwei Jungen und zwei Mädchen. Frau Kleinschmidt hat ihre Kinder entweder in einem Abstand von zwei oder von drei Jahren auf die Welt gebracht.  Bestimme den Median.
Bestimme den Median.  Den Median berechnest du, indem du die Summe der beiden mittleren Werte bildest und durch 2 dividierst: . Der Median für das Alter der Kinder der Familie Kleinschmidt beträgt somit 8 Jahre.
Den Median berechnest du, indem du die Summe der beiden mittleren Werte bildest und durch 2 dividierst: . Der Median für das Alter der Kinder der Familie Kleinschmidt beträgt somit 8 Jahre.
Sortieren
Als erstes musst du die Werte der Größe nach sortieren. Das Ergebnis nach dem Sortieren: 
Median bestimmen
Familie Kleinschmidt hat vier Kinder, das ist eine gerade Anzahl - du musst also den Median berechnen.

Mittelwert Die Summe aller vorliegenden Werte dividiert durch die Anzahl dieser Werte heißt Mittelwert. Der Trainer einer Basketball-Mannschaft misst die Körpergröße seiner Spieler. Berechne den Mittelwert. 
Mittelwert berechnen
Den Mittelwert berechnest du, indem du alle Körpergrößen der Spieler addierst und dann durch die Anzahl der Spieler dividierst: Die durchschnittliche Körpergröße aller Basketball-Spieler beträgt .
Median und Mittelwert im Vergleich In einem Autowerk werden jeden Tag ca. 450 Autos produziert. In einer Woche fallen am Mittwoch die Maschinen aus und stehen einen Tag still, am Donnerstag laufen sie mit halber Kraft. 
Der Median beträgt hier: 0, 225, 450, 450, 450.Der Mittelwert beträgt hier: .In diesem Fall eignet sich der Median besser, um die Autoproduktion an einem Tag zu beschreiben, da der Mittelwert den sonst üblichen Wert stark verändert.

