bettermarks » Mathebuch » Geometrie » Geometrie » Satzgruppe des Pythagoras » Berechnungen an Figuren und Körpern

Berechnungen an Figuren und Körpern

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?

bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.

Mehr erfahren

Hier erfährst du, wie du mit dem Satz des Pythagoras Streckenlängen in Figuren und Körpern berechnen kannst.

Höhe im gleichseitigen Dreieck
Diagonale im Quadrat
Raumdiagonale im Quader
Höhe einer Pyramide

Höhe im gleichseitigen Dreieck

In einem gleichseitigen Dreieck mit der Seitenlänge

a

und der Höhe

h

gilt:

h = \frac{a}{2} \sqrt{3}

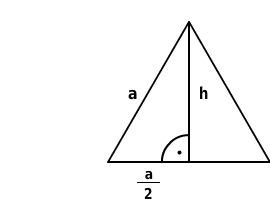
/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_1.jpg

Durch die Höhe wird das gleichseitige Dreieck in zwei kongruente rechtwinklige Dreiecke geteilt.Die Kathetenlängen sind

h

und

\frac{a}{2}

, die Hypotenusenlänge ist

a

Nach dem Satz des Pythagoras gilt:

a^{2} = h^{2} + {(\frac{a}{2})}^{2}

Du stellst nach

h^{2}

um, ziehst die Wurzel und vereinfachst so weit wie möglich:

Also:

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_3.jpg

Gleichseitiges Dreieck mit der Seitenlänge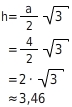

4 cm

Höhe h (in cm):

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_4.jpg

Diagonale im Quadrat

In einem Quadrat mit der Seitenlänge

a

gilt für die Länge der Diagonale

d

d = a \sqrt{2}

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_5.jpg

Die Diagonale

d

ist die Hypotenuse im rechtwinkligen Dreieck ABC. Die Katheten in diesem Dreieck sind die Seiten des Quadrats.

Nach dem Satz des Pythagoras gilt:

Du ziehst die Wurzel:

Quadrat mit der Seitenlänge

5 cm

Länge der Diagonale d (in cm):

Raumdiagonale im Quader

In einem Quader mit den Kantenlängen

a

b

und

c

gilt für die Länge der Raumdiagonale

d

d = \sqrt{a^{2} + b^{2} + c^{2}}

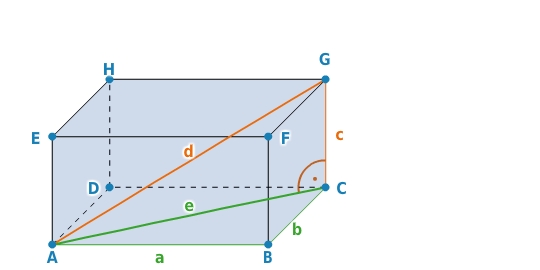
/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_9.jpg

Die Raumdiagonale

d

ist die Hypotenuse im rechtwinkligen Dreieck ACG, die Katheten sind die Seiten

c

und

e

Also:

d^{2} = e^{2} + c^{2}

Seite

e

wiederum ist die Hypotenuse im rechtwinkligen Dreieck ABC, mit den Katheten

a

und

b

Also:

e^{2} = a^{2} + b^{2}

Du setzt den Term auf der rechten Seite dieser Gleichung für

e^{2}

in der ersten Gleichung ein und ziehst anschließend die Wurzel:

Quader mit den Kantenlängen

2 cm

3 cm

und

4 cm

Länge der Raumdiagonale d (in cm):

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_11.jpg

Höhe einer Pyramide

Kennst du von einer vierseitigen Pyramide die Länge der Kanten, dann kannst du auch ihre Höhe berechnen.

Hierfür benötigst du zusätzlich eine der Diagonalen der rechteckigen Grundfläche.

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_12.jpg

Die Höhe ist im Dreieck AFS eine Kathete und es gilt:

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_13.jpg

Die Diagonale

e

ist im Dreieck ABC Hypotenuse und es gilt:

{(\frac{e}{2})}^{2} = {(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2}

Einsetzen ergibt:

h^{2} = s^{2} - ({(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2})

Also:

h = \sqrt{s^{2} - ({(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2})}

/wp-content/uploads/media/kem_GeoII_GeoIISGdPBFK_14.jpg

Höhe h (in cm):

Berechnungen an Figuren und Körpern

Höhe im gleichseitigen Dreieck

Diagonale im Quadrat

Raumdiagonale im Quader

Höhe einer Pyramide

Produkte

Unternehmen

Service