Ähnlichkeit von Figuren
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn dieser Erklärung erfährst du, wie du zwei Figuren auf ähnlichkeit überprüfen kannst.
ähnlichkeit von Figuren
Den Begriff ähnlich kennst du aus der Alltagssprache: Zwillinge sehen sich oft zum Verwechseln ähnlich, Mutter und Tochter sehen sich manchmal ähnlich und sogar Hund und Herrchen können sich verblüffend ähnlich sehen.  Auch in der Mathematik wird der Begriff verwendet, um die ähnlichkeit von Figuren auszudrücken. ähnliche Figuren haben die gleiche Form, unterscheiden sich jedoch in ihrer Größe und Lage. Aus einer Figur F erhältst du eine ähnliche Figur F‘, wenn du die Figur F mit einer zentrischen Streckung vergrößerst oder verkleinerst. Anschließend kannst du die Figur F' noch verschieben, drehen oder spiegeln. Es entsteht eine zu F ähnliche Figur F‘.
Auch in der Mathematik wird der Begriff verwendet, um die ähnlichkeit von Figuren auszudrücken. ähnliche Figuren haben die gleiche Form, unterscheiden sich jedoch in ihrer Größe und Lage. Aus einer Figur F erhältst du eine ähnliche Figur F‘, wenn du die Figur F mit einer zentrischen Streckung vergrößerst oder verkleinerst. Anschließend kannst du die Figur F' noch verschieben, drehen oder spiegeln. Es entsteht eine zu F ähnliche Figur F‘.

Figuren F und F‘ heißen zueinander ähnlich, wenn F durch eine zentrische Streckung so vergrößert oder verkleinert werden kann, dass eine zu F’ kongruente Figur entsteht.
Worin unterscheiden sich zwei ähnliche Figuren F und F‘ und worin stimmen sie überein? 

Zwei Figuren sind zueinander ähnlich, wenn

Sind die beiden Figuren zueinander ähnlich? 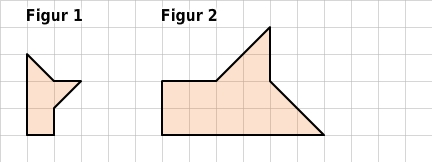

ähnlichkeit überprüfen
Alle Seiten von Figur 2 sind doppelt so lang wie die entsprechenden Seiten von Figur 1. Das Längenverhältnis der Seiten ist 2. Einander entsprechende Winkel sind in beiden Figuren gleich groß. Daher sind die Figuren ähnlich zueinander. 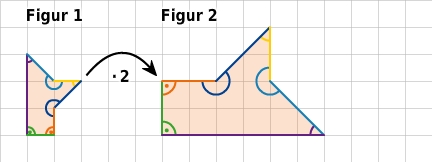

Ja, die beiden Figuren sind zueinander ähnlich.
Sind die beiden Vierecke zueinander ähnlich? 

ähnlichkeit überprüfen
Du vergleichst die Figuren und schaust, welche Winkel oder Seiten einander entsprechen könnten. Beide Figuren haben jeweils genau einen stumpfen Winkel (im Punkt A bzw. A’) und genau einen spitzen Winkel (im Punkt B bzw. B’). Wären beiden Figuren zueinander ähnlich, so würde der Punkt A dem Punkt A’, der Punkt B dem Punkt B’, der Punkt C dem Punkt C’ und der Punkt D dem Punkt D’ entsprechen. Dann wären jedoch die Längenverhältnisse einander entsprechender Seiten nicht gleich: 

Nein, die beiden Vierecke sind nicht zueinander ähnlich.
Ist diese Aussage wahr oder falsch? Alle Parallelogramme sind zueinander ähnlich.
Aussage überprüfen
Parallelogramme sind nicht immer zueinander ähnlich. Parallelogramme können zum Beispiel trotz gleicher Seitenlängen unterschiedlich große Winkel haben. 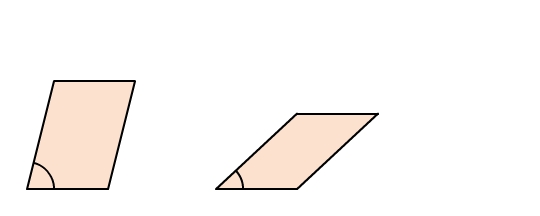

Die Aussage ist falsch.

