Ähnlichkeit von Dreiecken
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn dieser Erklärung erfährst du, wie du zwei Dreiecke auf Ähnlichkeit überprüfen kannst.
Die Ähnlichkeitssätze
Dreiecke spielen in der Mathematik eine wichtige Rolle.
Bestimmt hast du schon einmal einen Film gesehen, in dem Dinosaurier wie selbstverständlich durch die Szenen stampfen.
Hinter solchen Spezialeffekten steckt jede Menge Mathematik. Hier kommen Dreiecke ins Spiel:
Für den Dinosaurier wird ein Dreiecksnetz berechnet, das den Dino möglichst genau darstellt.
Erst mit Hilfe eines solchen Modells lässt sich der Dino im Film zum Leben erwecken.
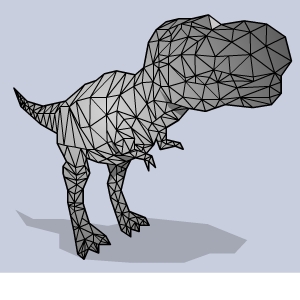
In der Abbildung erkennst du, dass das Dreiecksnetz aus verschiedenen Dreiecken besteht.
Sie unterscheiden sich in ihrer Größe, ihren Winkeln und in den Verhältnissen ihrer Seitenlängen.
Sicher findest du dort auch Dreiecke, die sich ähnlich sehen.
Im mathematischen Sinn ist „Ähnlichkeit“ aber nicht dem „Gefühl“ überlassen:
Zwei Dreiecke, die sich nur in ihrer Größe unterscheiden, nennt man zueinander ähnlich.
Die beiden blauen Dreiecke sind zueinander ähnlich.
Das orange Dreieck ist hingegen nicht ähnlich zu den anderen beiden Dreiecken.
Nur mit Augenmaß lässt sich nicht immer entscheiden, ob zwei Dreiecke zueinander ähnlich sind.
Um sicher zu gehen, überprüfst du ihre Winkel und Seitenverhältnisse.
Die Ähnlichkeitssätze erleichtern dir diese Arbeit.
Sie besagen, dass du nicht alle Seitenlängen und Winkel zu vergleichen brauchst.
Es genügt eine gezielte „Stichprobe“.
Ähnlichkeitssatz WW
Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei (und somit in allen drei) Winkeln übereinstimmen.
Weil du die Ähnlichkeit anhand zweier Winkel überprüfst, wird dieser Ähnlichkeitssatz kurz WW genannt.
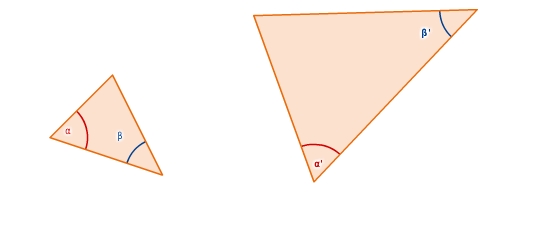
Zum Beispiel:
und
Ähnlichkeitssatz S:S:S
Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen der Längen entsprechender Seiten übereinstimmen.
Weil du die Ähnlichkeit anhand der Seitenverhältnisse überprüfst, wird dieser Ähnlichkeitssatz kurz S:S:S genannt.
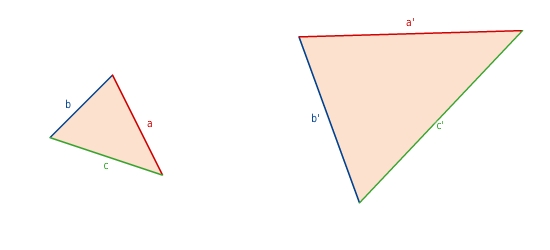
Du kannst auch in jedem der beiden Dreiecke zwei Seitenverhältnisse bilden und diese vergleichen.
Zum Beispiel:
und
Ähnlichkeitssatz S:W:S
Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel und im Verhältnis der Längen der anliegenden Seiten übereinstimmen.
Weil du die Ähnlichkeit anhand eines Seitenverhältnisses und anhand des eingeschlossenen Winkels überprüfst, wird dieser Ähnlichkeitssatz kurz S:W:S genannt.
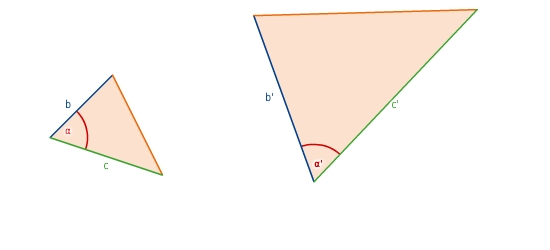
Zum Beispiel:
und
.
Du kannst auch einen Winkel und die Längenverhältnisse der entsprechenden anliegenden Seiten vergleichen.
Zum Beispiel:
und
.
Ähnlichkeitssatz S:s:W
Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis der Längen zweier Seiten und im Gegenwinkel der längeren Seite übereinstimmen.
Weil du die Ähnlichkeit anhand des Verhältnisses aus längerer zu kürzerer Seite und anhand des Gegenwinkels der längeren Seite überprüfst, wird dieser Ähnlichkeitssatz kurz S:s:W genannt.
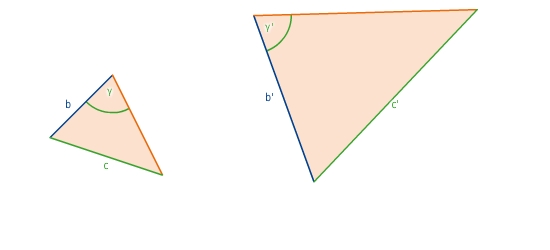
Zum Beispiel:
und
.
Du kannst auch zwei Längenverhältnisse entsprechender Seiten und den Gegenwinkel der größeren Seite vergleichen.
Zum Beispiel:
und
.
Dreiecke auf Ähnlichkeit überprüfen
Mit Hilfe der Ähnlichkeitssätze kannst du zwei Dreiecke auf Ähnlichkeit überprüfen.
Welchen Ähnlichkeitssatz du anwendest, hängt von den gegebenen Größen in den Dreiecken ab.
Sind die beiden Dreiecke zueinander ähnlich?
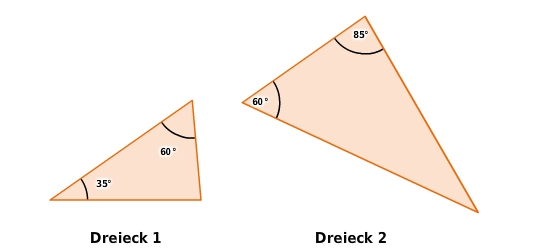
Ähnlichkeit überprüfen
Da in beiden Dreiecken zwei Winkel gegeben sind, untersuchst du, ob der Ähnlichkeitssatz WW erfüllt ist.
Beide Dreiecke haben einen Winkel von
.
Du überprüfst, ob sie in einem weiteren Winkel übereinstimmen.
Hierzu bestimmst du den dritten Winkel in Dreieck 1.
Da die Winkelsumme in jedem Dreieck
beträgt, gilt:
Beide Dreiecke haben einen Winkel von
.
Daher stimmen beide Dreiecke in zwei (und damit in drei) Winkeln überein und sind nach dem Ähnlichkeitssatz WW zueinander ähnlich.
Ja, die beiden Dreiecke sind zueinander ähnlich.
Sind die beiden Dreiecke zueinander ähnlich?
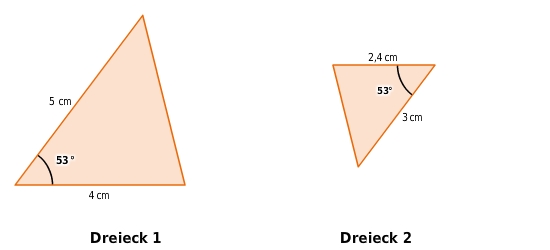
Ähnlichkeit überprüfen
Da in beiden Dreiecken jeweils ein Winkel und die Längen der anliegenden Schenkel gegeben sind,
untersuchst du, ob der Ähnlichkeitssatz S:W:S erfüllt ist.
Beide Dreiecke haben einen Winkel von
.
Du überprüfst, ob das Längenverhältnis der anliegenden Seiten in beiden Dreiecken gleich ist.
In Dreieck 1 ist das Längenverhältnis
.
In Dreieck 2 ist das Längenverhältnis
.
Nach dem Ähnlichkeitssatz S:W:S sind die Dreiecke zueinander ähnlich.
Ja, die beiden Dreiecke sind zueinander ähnlich.
Sind die beiden Dreiecke zueinander ähnlich?
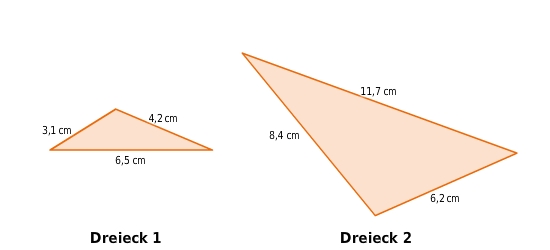
Ähnlichkeit überprüfen
Da in beiden Dreiecken alle Seitenlängen gegeben sind, überprüfst du die Längenverhältnisse entsprechender Seiten.
In ähnlichen Dreiecken sind diese Längenverhältnisse gleich.
Da die jeweils längsten Seiten ein anders Verhältnis besitzen als die beiden kürzesten Seiten,
sind die Dreiecke nicht zueinander ähnlich.
Nein, die beiden Dreiecke sind nicht zueinander ähnlich.
unbekannte Streckenlängen bestimmen
"Kennst du eines, kennst du alle!"
Du möchtest die Länge einer Strecke in einem Dreieck ABC bestimmen.
Die Strecke kannst du jedoch nicht berechnen, da du zu wenig über das Dreieck weißt.
Dann hilft es dir, ein ähnliches Dreieck zu finden, indem du die Längen der entsprechenden Strecken kennst.
Bestimme die Höhe h im rechtwinkligen Dreieck ABC.
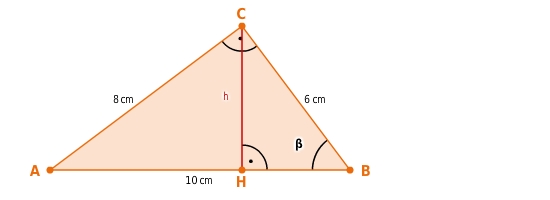
Ähnlichkeit nachweisen
Du zeigst zunächst, dass die Dreiecke ABC und BCH ähnlich zueinander sind.
Hierzu wendest du den Ähnlichkeitssatz WW an.
Die Dreiecke ABC und BCH haben den gemeinsamen Winkel
.
Außerdem sind beide Dreiecke rechtwinklig.
Die beiden Dreiecke stimmen in zwei Winkeln überein und sind nach dem Ähnlichkeitssatz WW zueinander ähnlich.
Höhe berechnen
Jetzt berechnest du die Höhe h:
Da die Dreiecke ABC und BCH zueinander ähnlich sind, stehen entsprechende Seitenlängen im selben Verhältnis zueinander.
Du ordnest die Seiten im Dreieck BCH den entsprechenden Seiten im Dreieck ABC zu, indem du die Seiten der Länge nach sortierst:
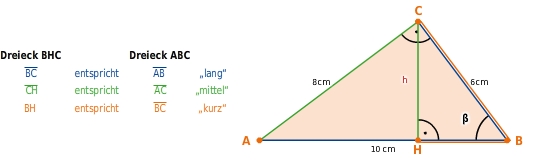Du bildest die Seitenverhältnisse:
und stellst die Verhältnisgleichung nach der gesuchten Strecke um.
Einsetzen der Werte:
Die gesuchte Strecke
ist
lag.
Du bildest die Seitenverhältnisse:
und stellst die Verhältnisgleichung nach der gesuchten Strecke um.
Einsetzen der Werte:
Die gesuchte Strecke
ist
lag.
h=
