Rechnen mit Wurzeltermen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit Wurzeltermen rechnest und welche Regeln du dabei beachten musst.
Definitionsbereich bestimmen
Der Radikand einer Wurzel ist nie negativ. Der maximale Definitionsbereich D von
besteht also aus allen positiven Zahlen und der Null.
Kurz:
ist definiert für alle x ≥ 0
Bestimme den Definitionsbereich D von
.
Definitionsbereich bestimmen
ist definiert für alle x, für die der Radikand positiv oder null ist.
Also
≥ 0.
Du kannst die Ungleichung umstellen:
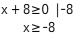
D = {x ∈ ℝ | x ≥ -8}
Bestimme den Definitionsbereich D von
.
Definitionsbereich bestimmen
Der Term
ist definiert für alle x, für die die Radikanden beider Wurzeln positiv oder null sind.
Also
≥ 0 und
≥ 0.
Du kannst beide Ungleichungen umstellen:
 Der Definitionsbereich enthält alle Zahlen, die beide Ungleichungen erfüllen. Diese kannst du in einer Ungleichungskette zusammenfassen.
D = {x ∈ ℝ | 3 le x le 5}
Der Definitionsbereich enthält alle Zahlen, die beide Ungleichungen erfüllen. Diese kannst du in einer Ungleichungskette zusammenfassen.
D = {x ∈ ℝ | 3 le x le 5}


D = {x ∈ ℝ | 3 le x le 5}
Bestimme den Definitionsbereich D von
.
Definitionsbereich bestimmen
Der Term
ist definiert für alle x, für die die Radikanden beider Wurzeln positiv oder null sind und zusätzlich der Nenner ungleich null ist.
Also: x ≥ 0 und
Du kannst die Ungleichung umstellen:
 Für x ≥ 0 gilt immer auch
. Also reicht die Einschränkung x ≥ 0 aus.
Für x ≥ 0 gilt immer auch
. Also reicht die Einschränkung x ≥ 0 aus.
 Für x ≥ 0 gilt immer auch
. Also reicht die Einschränkung x ≥ 0 aus.
Für x ≥ 0 gilt immer auch
. Also reicht die Einschränkung x ≥ 0 aus.
D = {x ∈ ℝ | x ≥ 0}
Multiplizieren und Dividieren
Multiplikation und Division zweier Wurzeln
Die Wurzel eines Produkts kannst du in das Produkt zweier Wurzeln umwandeln.
Multiplikationsregel:
für x, y ge 0
Ebenso kannst du die Wurzel eines Quotienten in den Quotienten zweier Wurzeln umwandeln.
Divisionsregel:
für x ge 0, y > 0
Für x ≥ 0 gilt:

Für x > 0 gilt:


Vereinfache
für alle x ≥ 0.
 Da x ≥ 0, kannst du die Betragsstriche weglassen.
Da x ≥ 0, kannst du die Betragsstriche weglassen.
Ausmultiplizieren
 Da x ≥ 0, kannst du die Betragsstriche weglassen.
Da x ≥ 0, kannst du die Betragsstriche weglassen.
Addieren und Subtrahieren
Für das Addieren und Subtrahieren von Wurzeln mit verschiedenen Radikanden gibt es keine Vereinfachungsregel.
≠
für x, y > 0 und
≠
für x > y > 0.
Du kannst auf eine Summe oder eine Differenz von Termen das Distributivgesetz anwenden und gleiche Wurzeln ausklammern.
für a, b, c ∈ ℝ und b > 0.
für x ≥ 0.
Teilweise Wurzelziehen
Mit Hilfe der Rechengesetze kannst du teilweise Wurzeln ziehen. Das bedeutet, den Radikanden in ein Produkt aus Quadraten und Termen, die keine Quadrate enthalten, zu zerlegen, um dann die Wurzel aus dem Produkt mit der Multiplikationsregel in ein Produkt aus Wurzeln zu zerlegen. Aus den Quadraten kannst du dann die Wurzel ziehen.
für y, x ≥ 0
Teilweise Wurzelziehen
für x ge 0

Vereinfache
für alle x, y ≥ 0.

 Da im Definitionsbereich x ≥ 0 angegeben ist, kannst du die Betragsstriche weglassen.
Da im Definitionsbereich x ≥ 0 angegeben ist, kannst du die Betragsstriche weglassen.
Rechengesetze anwenden

Wurzel teilweise ziehen
 Da im Definitionsbereich x ≥ 0 angegeben ist, kannst du die Betragsstriche weglassen.
Da im Definitionsbereich x ≥ 0 angegeben ist, kannst du die Betragsstriche weglassen.
Umgekehrt kannst du auch einen Faktor vor der Wurzel in den Radikanden multiplizieren, wenn du ihn dabei quadrierst.
für x, y ≥ 0.
für x ≥ 0
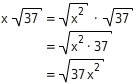
Brüche kürzen
Wie bei Zahlen kürzt du Brüche mit Wurzeln, indem du Zähler und Nenner durch einen gemeinsamen Faktor dividierst.
Durch Kürzen kann sich der Definitionsbereich des Terms ändern. Die angegebene Umformung gilt aber immer nur für den „kleineren“ der beiden Definitionsbereiche.
Kürze den Term
für x ≠
.
Du verwendest die dritte binomische Formel:
mit
und
:
 Der Definitionsbereich hat sich durch die Umformung geändert:
Der Term auf der linken Seite ist auf
{
} definiert, der Term auf der rechten Seite für alle reellen Zahlen.
Die äquivalenz gilt also nur für x ∈ D.
Der Definitionsbereich hat sich durch die Umformung geändert:
Der Term auf der linken Seite ist auf
{
} definiert, der Term auf der rechten Seite für alle reellen Zahlen.
Die äquivalenz gilt also nur für x ∈ D.
 Der Definitionsbereich hat sich durch die Umformung geändert:
Der Term auf der linken Seite ist auf
{
} definiert, der Term auf der rechten Seite für alle reellen Zahlen.
Die äquivalenz gilt also nur für x ∈ D.
Der Definitionsbereich hat sich durch die Umformung geändert:
Der Term auf der linken Seite ist auf
{
} definiert, der Term auf der rechten Seite für alle reellen Zahlen.
Die äquivalenz gilt also nur für x ∈ D.

