Begründen und Beweisen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, wie du den Satz des Pythagoras beweisen kannst.Der Satz ist nach Pythagoras von Samos (* um 570 v. Chr.; † nach 510 v. Chr.) benannt.
Er war aber schon lange vor Pythagoras bekannt.Die Babylonier und ägypter haben bereits um 1600 v. Chr. die Zusammenhänge am rechtwinkligen Dreieck erkannt und sie als selbstverständlich hingenommen.
Begründen und beweisen
Ein Beweis ist eine logische Begründung mit Allgemeingültigkeit.
Möchtest du zum Beispiel den Satz des Pythagoras beweisen, so genügt es nicht, die Gleichung
an einigen rechtwinkligen Dreiecken exemplarisch nachzuprüfen.
Auch die Begründung „Es wurde noch kein Gegenbeispiel gefunden“ reicht nicht aus.
Die Gültigkeit des Satzes muss für alle rechtwinkligen Dreiecke nachgewiesen werden, erst dann handelt es sich um einen mathematischen Beweis.
Es gibt Hunderte von Beweisen des Satzes des Pythagoras, die teilweise aber nur sehr wenig voneinander abweichen.
Daher werden schon lang bekannte Beweise auch immer wieder neu entdeckt.
Einer dieser Beweise wird Leonardo da Vinci zugesprochen und auch der amerikanische Präsident James Abraham Garfield hat einen Beweis geliefert.
Altindischer „Stuhl der Braut“.
Der Satz des Pythagoras wird hier folgendermaßen interpretiert:
Aus zwei Quadraten (die Kathetenquadrate) wird durch Zerlegung ein Quadrat (das Hypotenusenquadrat).
Abgeschnitten wird jeweils genau das rechtwinklige Dreieck, zu dem die Katheten und die Hypotenuse gehören.
Die Animation veranschaulicht die Beweisidee.
Diese Zerlegung der Kathetenquadrate in Einzelteile, die sich zum Hypotenusenquadrat neu zusammensetzen lassen, funktioniert für alle rechtwinkligen Dreiecke.
Ergänzungsbeweis
Dieser Beweis hat seinen Ursprung vermutlich auch im alten Indien.
Die Idee ist, einerseits das Hypotenusenquadrat und andererseits die beiden Kathetenquadrate durch jeweils vier identische Dreiecke so zu ergänzen, dass zwei gleich große Quadrate entstehen.
Gegeben ist das rechtwinklige Dreieck mit den Katheten a und b und der Hypotenuse c (Ausgangsdreieck).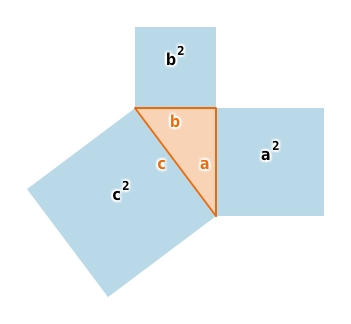 Du betrachtest diese beiden Figuren.
Figur 1 entsteht, indem du das Hypotenusenquadrat ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.Figur 2 entsteht, indem du die beiden Kathetenquadrate ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.
Du betrachtest diese beiden Figuren.
Figur 1 entsteht, indem du das Hypotenusenquadrat ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.Figur 2 entsteht, indem du die beiden Kathetenquadrate ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.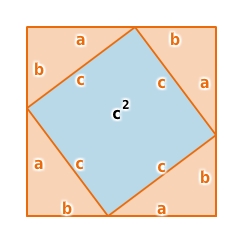
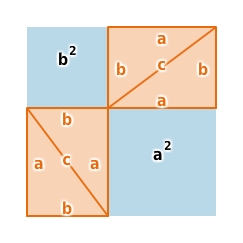 In beiden Figuren ergänzen sich blaue und orange Flächen zu demselben Quadrat mit der Seitenlänge a+b.
Da die orange Fläche (vier kongruente Dreiecke) in beiden Figuren gleich groß ist, ist auch die blaue Fläche in beiden Figuren gleich groß ist. Also sind die beiden Kathetenquadrate zusammen genauso groß wie das Hypotenusenquadrat.
Das funktioniert aber nur, wenn das Ausgangsdreieck rechtwinklig ist.
Ist es nicht rechtwinklig, so ergänzen sich blaue und orange Flächen nicht zu einem Quadrat, sondern zu einem Achteck.
In beiden Figuren ergänzen sich blaue und orange Flächen zu demselben Quadrat mit der Seitenlänge a+b.
Da die orange Fläche (vier kongruente Dreiecke) in beiden Figuren gleich groß ist, ist auch die blaue Fläche in beiden Figuren gleich groß ist. Also sind die beiden Kathetenquadrate zusammen genauso groß wie das Hypotenusenquadrat.
Das funktioniert aber nur, wenn das Ausgangsdreieck rechtwinklig ist.
Ist es nicht rechtwinklig, so ergänzen sich blaue und orange Flächen nicht zu einem Quadrat, sondern zu einem Achteck.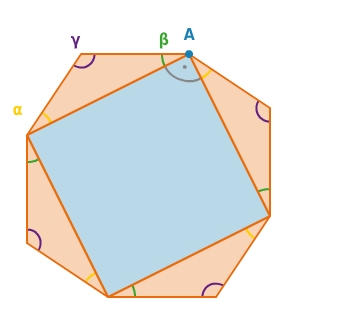 Wieso entsteht eine Ecke im Punkt A?
In dem Ausgangsdreieck gilt
. Daraus folgt
. Also ergeben der rechte Winkel im Punkt A zusammen mit den Winkeln
und
keinen gestreckten Winkel. Es entsteht eine Ecke.
Wieso entsteht eine Ecke im Punkt A?
In dem Ausgangsdreieck gilt
. Daraus folgt
. Also ergeben der rechte Winkel im Punkt A zusammen mit den Winkeln
und
keinen gestreckten Winkel. Es entsteht eine Ecke.
 Du betrachtest diese beiden Figuren.
Figur 1 entsteht, indem du das Hypotenusenquadrat ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.Figur 2 entsteht, indem du die beiden Kathetenquadrate ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.
Du betrachtest diese beiden Figuren.
Figur 1 entsteht, indem du das Hypotenusenquadrat ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.Figur 2 entsteht, indem du die beiden Kathetenquadrate ergänzt durch vier Dreiecke, die kongruent sind zum Ausgangsdreieck.
 In beiden Figuren ergänzen sich blaue und orange Flächen zu demselben Quadrat mit der Seitenlänge a+b.
Da die orange Fläche (vier kongruente Dreiecke) in beiden Figuren gleich groß ist, ist auch die blaue Fläche in beiden Figuren gleich groß ist. Also sind die beiden Kathetenquadrate zusammen genauso groß wie das Hypotenusenquadrat.
Das funktioniert aber nur, wenn das Ausgangsdreieck rechtwinklig ist.
Ist es nicht rechtwinklig, so ergänzen sich blaue und orange Flächen nicht zu einem Quadrat, sondern zu einem Achteck.
In beiden Figuren ergänzen sich blaue und orange Flächen zu demselben Quadrat mit der Seitenlänge a+b.
Da die orange Fläche (vier kongruente Dreiecke) in beiden Figuren gleich groß ist, ist auch die blaue Fläche in beiden Figuren gleich groß ist. Also sind die beiden Kathetenquadrate zusammen genauso groß wie das Hypotenusenquadrat.
Das funktioniert aber nur, wenn das Ausgangsdreieck rechtwinklig ist.
Ist es nicht rechtwinklig, so ergänzen sich blaue und orange Flächen nicht zu einem Quadrat, sondern zu einem Achteck. Wieso entsteht eine Ecke im Punkt A?
In dem Ausgangsdreieck gilt
. Daraus folgt
. Also ergeben der rechte Winkel im Punkt A zusammen mit den Winkeln
und
keinen gestreckten Winkel. Es entsteht eine Ecke.
Wieso entsteht eine Ecke im Punkt A?
In dem Ausgangsdreieck gilt
. Daraus folgt
. Also ergeben der rechte Winkel im Punkt A zusammen mit den Winkeln
und
keinen gestreckten Winkel. Es entsteht eine Ecke.
Neben den geometrischen Beweisen gibt es auch algebraische Beweise für den Satz des Pythagoras.
In einem solchen Beweis wird eine Gleichung aufgestellt, aus der die Gleichung
folgt.
Gegeben ist das rechtwinklige Dreieck mit den Kathetenlängen a und b und der Hypotenusenlänge c (Ausgangsdreieck).
Du möchtest die Gleichung
herleiten. Hierzu setzt du vier Kopien des Ausgangsdreiecks zu der folgenden Figur zusammen:
Hierzu setzt du vier Kopien des Ausgangsdreiecks zu der folgenden Figur zusammen: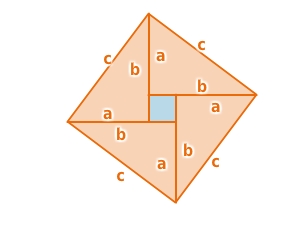 Es entsteht ein Quadrat (in Blau) in der Mitte der Figur. Dieses Quadrat hat die Seitenlänge b-a:
Es entsteht ein Quadrat (in Blau) in der Mitte der Figur. Dieses Quadrat hat die Seitenlänge b-a: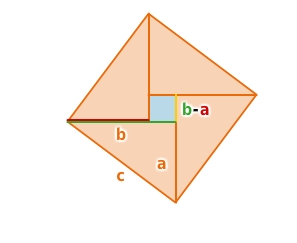 Der Flächeninhalt des großen Quadrats ist gleich der Summe der Flächeninhalte seiner Teilflächen.
Du berechnest die einzelnen Flächeninhalte:
Flächeinhalt des großen Quadrats:
Flächeninhalt eines Dreiecks (in Orange):
Flächeninhalt aller vier Dreiecke zusammen:
Flächeninhalt des kleinen Quadrats (in Blau):
Also gilt:
Mit Hilfe der zweiten binomischen Formel vereinfachst du die Gleichung:
und erhältst die Formel
.
An welcher Stelle wird in diesem Beweis eigentlich verwendet, dass das Ausgangsdreieck rechtwinklig ist"
Zur Beantwortung dieser Frage versuchst du, den Beweis auf ein nicht rechtwinkliges Dreieck zu übertragen. In diesem Beispiel gilt
.
Der Flächeninhalt des großen Quadrats ist gleich der Summe der Flächeninhalte seiner Teilflächen.
Du berechnest die einzelnen Flächeninhalte:
Flächeinhalt des großen Quadrats:
Flächeninhalt eines Dreiecks (in Orange):
Flächeninhalt aller vier Dreiecke zusammen:
Flächeninhalt des kleinen Quadrats (in Blau):
Also gilt:
Mit Hilfe der zweiten binomischen Formel vereinfachst du die Gleichung:
und erhältst die Formel
.
An welcher Stelle wird in diesem Beweis eigentlich verwendet, dass das Ausgangsdreieck rechtwinklig ist"
Zur Beantwortung dieser Frage versuchst du, den Beweis auf ein nicht rechtwinkliges Dreieck zu übertragen. In diesem Beispiel gilt
. Du setzt vier Kopien dieses Dreiecks zu der folgenden Figur zusammen:
Du setzt vier Kopien dieses Dreiecks zu der folgenden Figur zusammen: 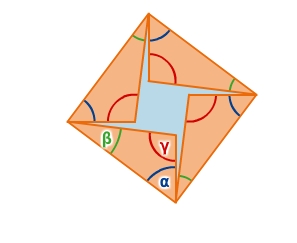 In der Mitte der Figur entsteht kein Quadrat(in Blau). Denn aus
folgt
. Also füllen zwei benachbarte Dreiecke nicht die rechtwinkligen Ecken des großen Quadrats aus.
In der Mitte der Figur entsteht kein Quadrat(in Blau). Denn aus
folgt
. Also füllen zwei benachbarte Dreiecke nicht die rechtwinkligen Ecken des großen Quadrats aus.
 Hierzu setzt du vier Kopien des Ausgangsdreiecks zu der folgenden Figur zusammen:
Hierzu setzt du vier Kopien des Ausgangsdreiecks zu der folgenden Figur zusammen: Es entsteht ein Quadrat (in Blau) in der Mitte der Figur. Dieses Quadrat hat die Seitenlänge b-a:
Es entsteht ein Quadrat (in Blau) in der Mitte der Figur. Dieses Quadrat hat die Seitenlänge b-a: Der Flächeninhalt des großen Quadrats ist gleich der Summe der Flächeninhalte seiner Teilflächen.
Du berechnest die einzelnen Flächeninhalte:
Flächeinhalt des großen Quadrats:
Flächeninhalt eines Dreiecks (in Orange):
Flächeninhalt aller vier Dreiecke zusammen:
Flächeninhalt des kleinen Quadrats (in Blau):
Also gilt:
Mit Hilfe der zweiten binomischen Formel vereinfachst du die Gleichung:
und erhältst die Formel
.
An welcher Stelle wird in diesem Beweis eigentlich verwendet, dass das Ausgangsdreieck rechtwinklig ist"
Zur Beantwortung dieser Frage versuchst du, den Beweis auf ein nicht rechtwinkliges Dreieck zu übertragen. In diesem Beispiel gilt
.
Der Flächeninhalt des großen Quadrats ist gleich der Summe der Flächeninhalte seiner Teilflächen.
Du berechnest die einzelnen Flächeninhalte:
Flächeinhalt des großen Quadrats:
Flächeninhalt eines Dreiecks (in Orange):
Flächeninhalt aller vier Dreiecke zusammen:
Flächeninhalt des kleinen Quadrats (in Blau):
Also gilt:
Mit Hilfe der zweiten binomischen Formel vereinfachst du die Gleichung:
und erhältst die Formel
.
An welcher Stelle wird in diesem Beweis eigentlich verwendet, dass das Ausgangsdreieck rechtwinklig ist"
Zur Beantwortung dieser Frage versuchst du, den Beweis auf ein nicht rechtwinkliges Dreieck zu übertragen. In diesem Beispiel gilt
. Du setzt vier Kopien dieses Dreiecks zu der folgenden Figur zusammen:
Du setzt vier Kopien dieses Dreiecks zu der folgenden Figur zusammen:  In der Mitte der Figur entsteht kein Quadrat(in Blau). Denn aus
folgt
. Also füllen zwei benachbarte Dreiecke nicht die rechtwinkligen Ecken des großen Quadrats aus.
In der Mitte der Figur entsteht kein Quadrat(in Blau). Denn aus
folgt
. Also füllen zwei benachbarte Dreiecke nicht die rechtwinkligen Ecken des großen Quadrats aus.
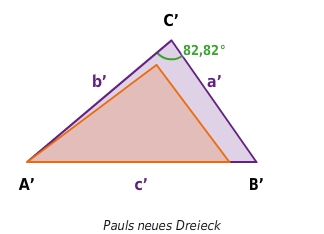
Leonie und Paul haben als Vorlage dasselbe rechtwinklige Ausgangsdreieck ABC mit den Seitenlängen
,
,
.
Leonie verdoppelt alle Seiten des Ausgangsdreiecks. Paul hingegen verlängert die Seiten des Ausgangsdreiecks jeweils um
.
Sind die beiden neuen Dreiecke rechtwinklig?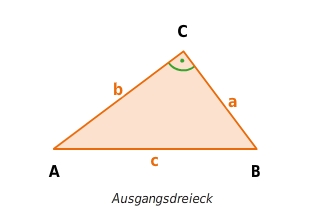 Leonies neues Dreieck ist rechtwinklig, Pauls Dreieck ist nicht rechtwinklig.
Begründung:Leonie verdoppelt alle Seiten des Augangsdreiecks und erhält ein neues Dreieck mit den Seitenlängen a’=
, b’=
und c’=
.
Du überprüfst, ob die Gleichung
für diese Werte erfüllt ist:
Leonies neues Dreieck ist rechtwinklig, Pauls Dreieck ist nicht rechtwinklig.
Begründung:Leonie verdoppelt alle Seiten des Augangsdreiecks und erhält ein neues Dreieck mit den Seitenlängen a’=
, b’=
und c’=
.
Du überprüfst, ob die Gleichung
für diese Werte erfüllt ist: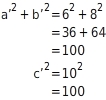 also:
(übrigens: Dass Leonies neues Dreieck A’B’C’ rechtwinklig ist, kannst du auch mit dem Ähnlichkeitssatz S:S:S begründen.
Das Dreieck A’B’C’ entsteht aus dem Dreieck ABC durch Verdopplung der Seiten, also sind die beiden Dreiecke zueinander ähnlich.
Insbesondere hat das Dreieck A’B’C’ dieselben Winkel wie das Dreieck ABC und ist deshalb auch rechtwinklig.)
also:
(übrigens: Dass Leonies neues Dreieck A’B’C’ rechtwinklig ist, kannst du auch mit dem Ähnlichkeitssatz S:S:S begründen.
Das Dreieck A’B’C’ entsteht aus dem Dreieck ABC durch Verdopplung der Seiten, also sind die beiden Dreiecke zueinander ähnlich.
Insbesondere hat das Dreieck A’B’C’ dieselben Winkel wie das Dreieck ABC und ist deshalb auch rechtwinklig.)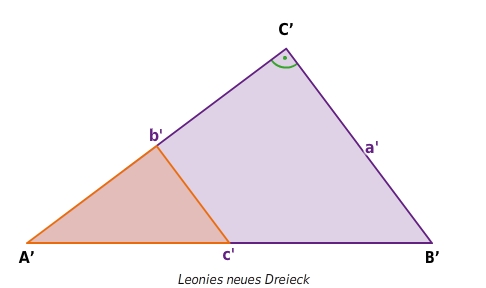 Paul verlängert alle Seiten des Ausgangsdreiecks um einen Zentimeter und erhält ein neues Dreieck mit den Seitenlängen
,
,
.
Wäre dieses Dreieck rechtwinklig, so käme als Hypotenuse nur die längste Seite c’ in Frage.
Außerdem müsste nach dem Satz des Pythagoras die Gleichung
erfüllt sein:
Paul verlängert alle Seiten des Ausgangsdreiecks um einen Zentimeter und erhält ein neues Dreieck mit den Seitenlängen
,
,
.
Wäre dieses Dreieck rechtwinklig, so käme als Hypotenuse nur die längste Seite c’ in Frage.
Außerdem müsste nach dem Satz des Pythagoras die Gleichung
erfüllt sein: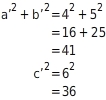 also:
≠
also:
≠
 Leonies neues Dreieck ist rechtwinklig, Pauls Dreieck ist nicht rechtwinklig.
Begründung:Leonie verdoppelt alle Seiten des Augangsdreiecks und erhält ein neues Dreieck mit den Seitenlängen a’=
, b’=
und c’=
.
Du überprüfst, ob die Gleichung
für diese Werte erfüllt ist:
Leonies neues Dreieck ist rechtwinklig, Pauls Dreieck ist nicht rechtwinklig.
Begründung:Leonie verdoppelt alle Seiten des Augangsdreiecks und erhält ein neues Dreieck mit den Seitenlängen a’=
, b’=
und c’=
.
Du überprüfst, ob die Gleichung
für diese Werte erfüllt ist: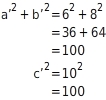 also:
(übrigens: Dass Leonies neues Dreieck A’B’C’ rechtwinklig ist, kannst du auch mit dem Ähnlichkeitssatz S:S:S begründen.
Das Dreieck A’B’C’ entsteht aus dem Dreieck ABC durch Verdopplung der Seiten, also sind die beiden Dreiecke zueinander ähnlich.
Insbesondere hat das Dreieck A’B’C’ dieselben Winkel wie das Dreieck ABC und ist deshalb auch rechtwinklig.)
also:
(übrigens: Dass Leonies neues Dreieck A’B’C’ rechtwinklig ist, kannst du auch mit dem Ähnlichkeitssatz S:S:S begründen.
Das Dreieck A’B’C’ entsteht aus dem Dreieck ABC durch Verdopplung der Seiten, also sind die beiden Dreiecke zueinander ähnlich.
Insbesondere hat das Dreieck A’B’C’ dieselben Winkel wie das Dreieck ABC und ist deshalb auch rechtwinklig.) Paul verlängert alle Seiten des Ausgangsdreiecks um einen Zentimeter und erhält ein neues Dreieck mit den Seitenlängen
,
,
.
Wäre dieses Dreieck rechtwinklig, so käme als Hypotenuse nur die längste Seite c’ in Frage.
Außerdem müsste nach dem Satz des Pythagoras die Gleichung
erfüllt sein:
Paul verlängert alle Seiten des Ausgangsdreiecks um einen Zentimeter und erhält ein neues Dreieck mit den Seitenlängen
,
,
.
Wäre dieses Dreieck rechtwinklig, so käme als Hypotenuse nur die längste Seite c’ in Frage.
Außerdem müsste nach dem Satz des Pythagoras die Gleichung
erfüllt sein: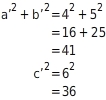 also:
≠
also:
≠


