Größen berechnen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du in Strahlensatzfiguren unbekannte Streckenlängen mit Hilfe der beiden Strahlensätze berechnest.
Streckenlängen in der V-Figur berechnen
Einzelne Streckenlängen innerhalb einer Strahlensatzfigur berechnest du, indem du, je nachdem, welche Strecken gegeben sind, eine Verhältnisgleichung mit einem der beiden Strahlensätze aufstellst und die Gleichung nach der unbekannten Streckenlänge auflöst.

Um in dieser Figur
zu berechnen, verwendest du den ersten Strahlensatz:
. Für
kannst du den zweiten Strahlensatz verwenden:
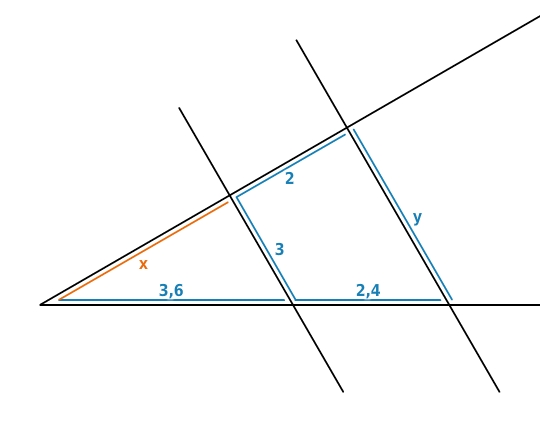
Wähle die zur Strahlensatzfigur passende Verhältnisgleichung und berechne
. (Maße in cm)
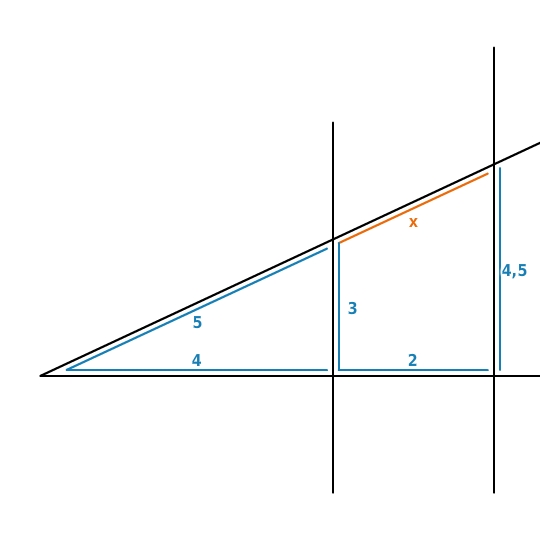
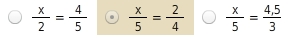

Verhältnisgleichung wählen
In der ersten Gleichung wurden nicht die entsprechenden Strahlenabschnitte gewählt. In der dritten Gleichung könntest du den zweiten Strahlensatz vermuten, da hier die Parallelenabschnitte verwendet werden, aber die Strecke
kommt im zweiten Strahlensatz nicht als Strahlenabschnitt vor.
berechnen
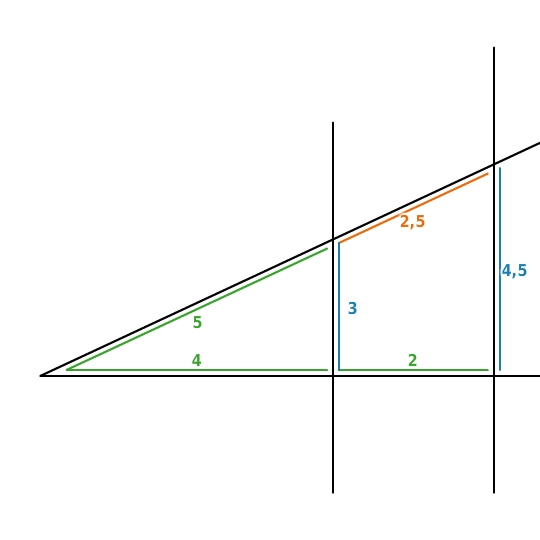
Du berechnest
, indem du die Verhältnisgleichung nach
auflöst:
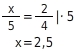
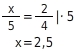

Berechne die Streckenlängen
und
. (Maße in dm)
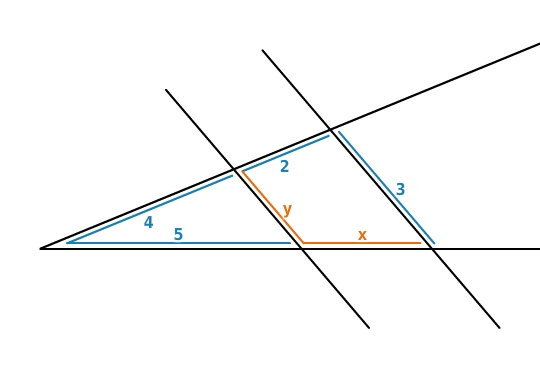

Streckenlängen berechnen
Um
zu berechnen, verwendest du den ersten Strahlensatz. Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
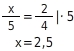
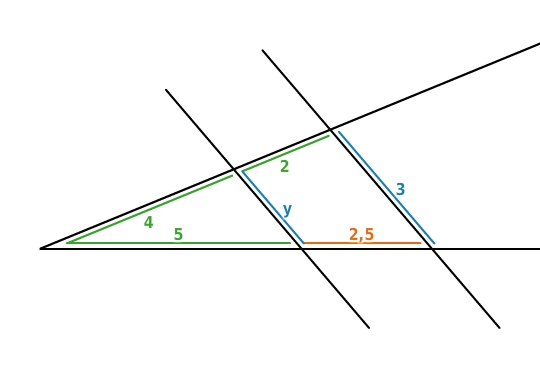 Um
zu berechnen, verwendest du den zweiten Strahlensatz.
Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
Um
zu berechnen, verwendest du den zweiten Strahlensatz.
Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
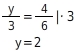
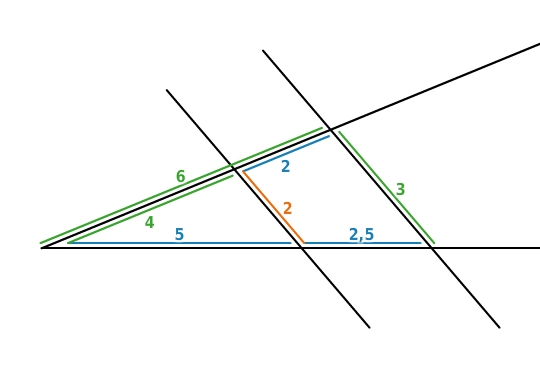
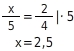
 Um
zu berechnen, verwendest du den zweiten Strahlensatz.
Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
Um
zu berechnen, verwendest du den zweiten Strahlensatz.
Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
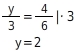

Bestimme die Streckenlänge
mit Hilfe der Verhältnisgleichung:
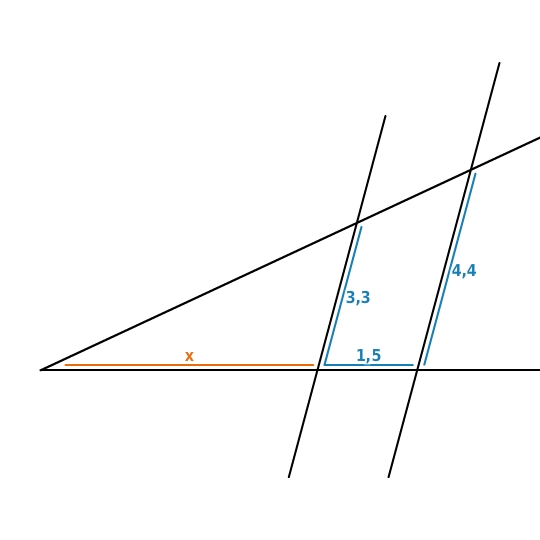
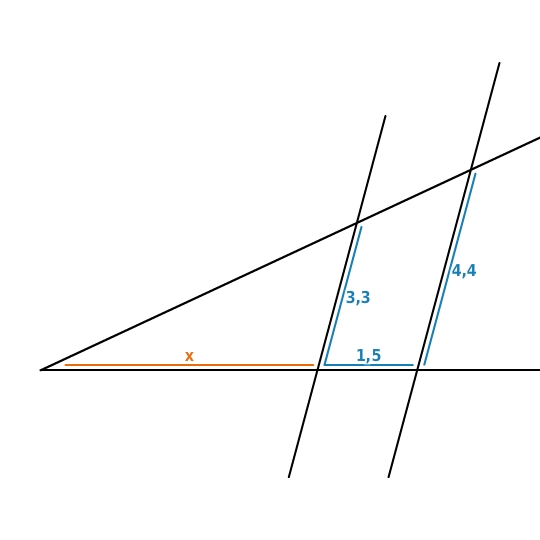
berechnen
Die Gleichung löst du nach
auf:
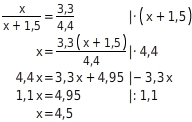
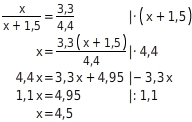
Streckenlängen in der X-Figur berechnen
Einzelne Streckenlängen innerhalb einer Strahlensatzfigur berechnest du, indem du, je nachdem, welche Strecken gegeben sind, eine Verhältnisgleichung mit einem der beiden Strahlensätze aufstellst und die Gleichung nach der unbekannten Streckenlänge auflöst.
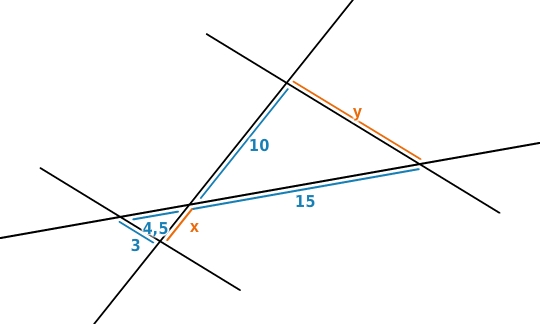

Um in dieser Figur
zu berechnen, verwendest du den ersten Strahlensatz:
.
Für
kannst du den zweiten Strahlensatz verwenden:
Wähle die zur Strahlensatzfigur passende Verhältnisgleichung und berechne
. (Maße in cm)
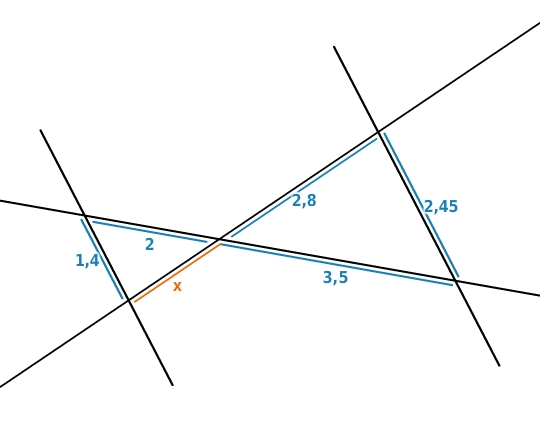
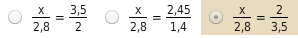

Verhältnisgleichung wählen
In der ersten Gleichung wurden nicht die entsprechenden Geradenabschnitte gewählt.
In der zweiten Gleichung könntest du den zweiten Strahlensatz vermuten, da hier die Parallelenabschnitte verwendet werden, aber diese wurden falsch zugeordnet.
berechnen
Du berechnest
, indem du die Verhältnisgleichung nach
auflöst:
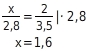
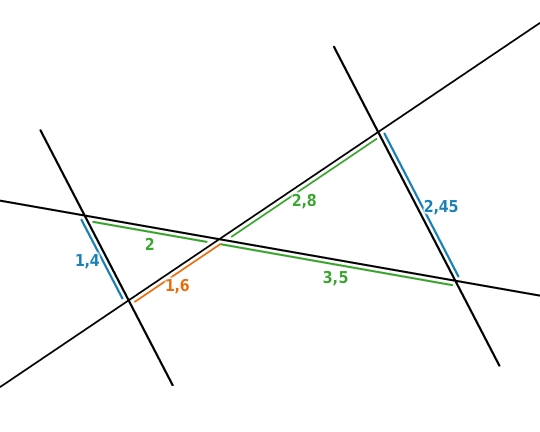
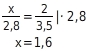

Berechne die Streckenlängen
und
. (Maße in cm)
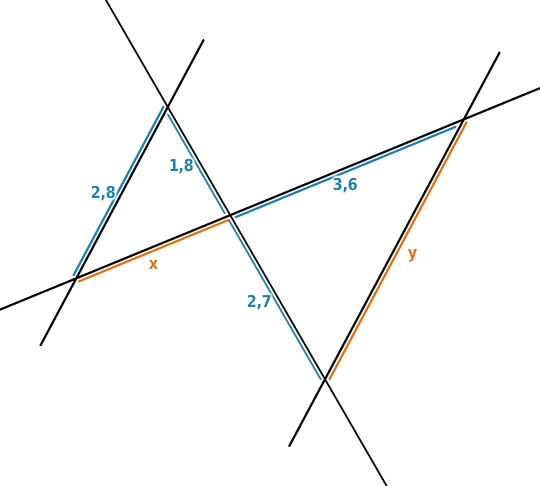

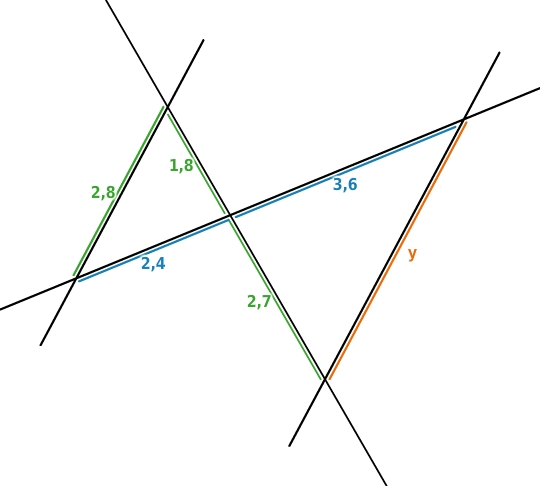
Streckenlängen berechnen
In dieser Strahlensatzfigur ist es egal welche Streckenlänge du zuerst berechnest.
Um
zu berechnen, verwendest du den ersten Strahlensatz. Zunächst stellst du eine Verhältnisgleichung auf und löst sie anschließend nach
auf:
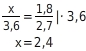
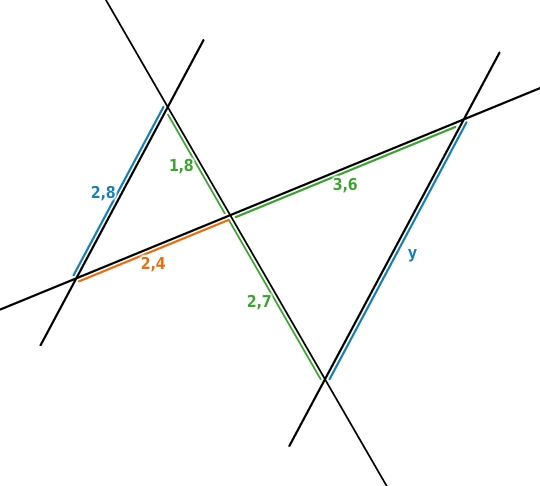 Um
zu berechnen, verwendest du den zweiten Strahlensatz. Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
Um
zu berechnen, verwendest du den zweiten Strahlensatz. Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
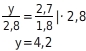
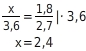
 Um
zu berechnen, verwendest du den zweiten Strahlensatz. Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
Um
zu berechnen, verwendest du den zweiten Strahlensatz. Du stellst eine Verhältnisgleichung auf und löst sie nach
auf:
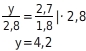

Berechne die Streckenlängen
und
. (Maße in cm)
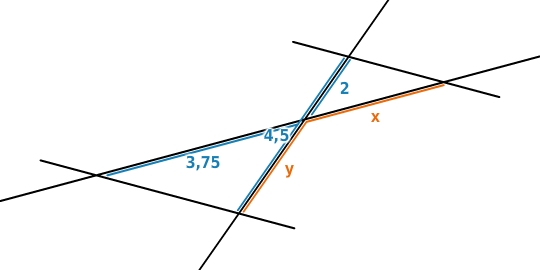

Streckenlängen berechnen
Um
zu berechnen, benötigst du
:
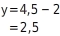 Du kannst nun
berechnen, indem du eine Verhältnisgleichung aufstellst und diese dann nach
auflöst:
Du kannst nun
berechnen, indem du eine Verhältnisgleichung aufstellst und diese dann nach
auflöst:
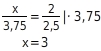
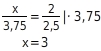
Umkehrsatz des ersten Strahlensatzes
Die Strahlensätze sind in der Wenn-Dann-Form formuliert. Erster Strahlensatz (V-Figur):
Wenn zwei Strahlen mit gemeinsamem Anfangspunkt von zwei Parallelen geschnitten werden, dann verhalten sich je zwei Abschnitte auf dem einen Strahl wie die entsprechenden Abschnitte auf dem anderen Strahl.
Durch Vertauschung von Voraussetzung (Wenn-Teil) und Behauptung (Dann-Teil) erhältst du den ebenfalls gültigen Umkehrsatz:
Wenn zwei Strahlen mit gemeinsamem Anfangspunkt von zwei Geraden geschnitten werden und sich je zwei Abschnitte auf dem einen Strahl wie die entsprechenden Abschnitte auf dem anderen Strahl verhalten, dann sind die beiden Geraden zueinander parallel.
überprüfe rechnerisch, welche Geraden parallel sind.
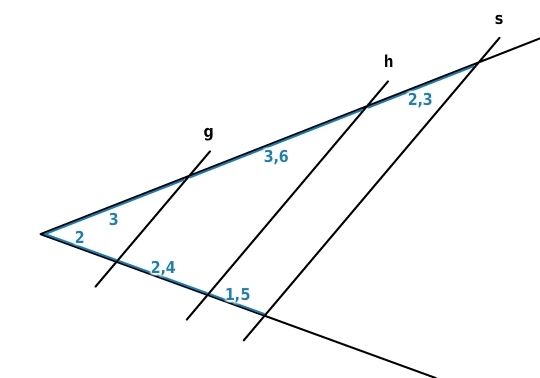

Die Parallelität der Geraden g, h und s prüfst du, indem du nach dem ersten Strahlensatz die Verhältnisse aufstellst und ihre Gleichheit überprüfst.
Geraden g und h:
 Die Gleichheit ist erfüllt, also sind die Geraden g und h nach dem Umkehrsatz parallel.
Geraden g und s:
≠
Die Gleichheit ist erfüllt, also sind die Geraden g und h nach dem Umkehrsatz parallel.
Geraden g und s:
≠
 Die Gleichheit ist nicht erfüllt, also sind die Geraden g und s nicht parallel.
Geraden h und s:
≠
Die Gleichheit ist nicht erfüllt, also sind die Geraden g und s nicht parallel.
Geraden h und s:
≠
 Die Gleichheit ist nicht erfüllt, also sind die Geraden h und s nicht parallel.
Die Gleichheit ist nicht erfüllt, also sind die Geraden h und s nicht parallel.
Die Geraden
 sind parallel.
Die Geraden g und h sind parallel.
sind parallel.
Die Geraden g und h sind parallel.
Die Umkehrung des zweiten Strahlensatzes gilt nicht.
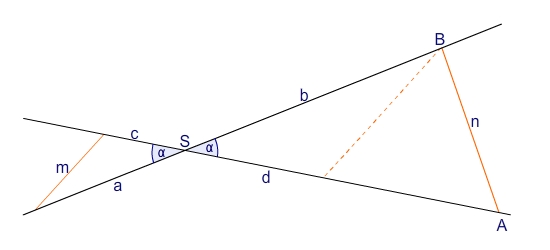
Wenn eine Figur wie oben z.B. mit den Maßen
,
,
,
und
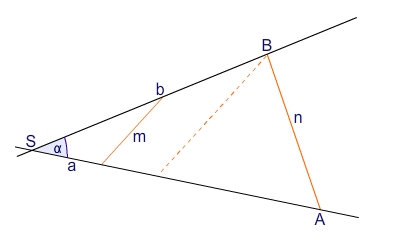
angefertigt werden soll, dann ist das Dreieck ABS nicht eindeutig konstruierbar.
Es sind zwar die Seiten b und n sowie der Winkel
gegeben, allerdings ist der Kongruenzsatz SsW nicht erfüllt, da der Winkel
der kürzeren Seite n gegenüber liegt. Damit ist die Eindeutigkeit nicht gegeben.
Die Strahlensätze sind in der Wenn-Dann-Form formuliert. Erster Strahlensatz (X-Figur):
Wenn zwei Geraden mit einem Schnittpunkt von zwei Parallelen geschnitten werden, dann verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.
Wenn du die Voraussetzung (Wenn-Teil) und Behauptung (Dann-Teil) vertauschst, dann erhältst du den ebenfalls gültigen Umkehrsatz:
Wenn zwei Geraden mit einem Schnittpunkt von zwei Geraden geschnitten werden und sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden verhalten, dann sind die beiden Geraden, die die zwei sich schneidenden Geraden schneiden, zueinander parallel.
überprüfe rechnerisch, welche Geraden parallel sind.
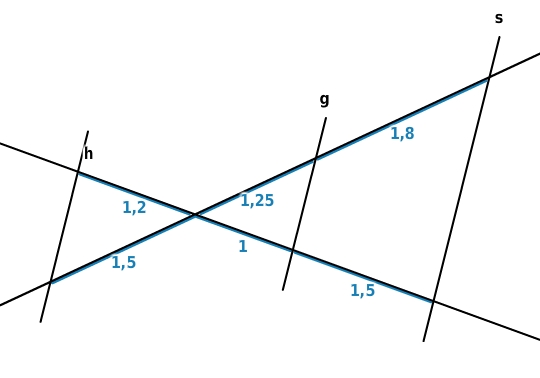

Die Parallelität der Geraden g, h und s prüfst du, indem du nach dem ersten Strahlensatz die Verhältnisse aufstellst und ihre Gleichheit überprüfst.
Geraden g und h:
 Die Gleichheit ist erfüllt, also sind die Geraden g und h nach dem Umkehrsatz parallel.
Geraden g und s:
≠
Die Gleichheit ist erfüllt, also sind die Geraden g und h nach dem Umkehrsatz parallel.
Geraden g und s:
≠
 Die Gleichheit ist nicht erfüllt, also sind die Geraden g und s nicht parallel.
Geraden h und s:
≠
Die Gleichheit ist nicht erfüllt, also sind die Geraden g und s nicht parallel.
Geraden h und s:
≠
 Die Gleichheit ist nicht erfüllt, also sind die Geraden h und s nicht parallel.
Die Gleichheit ist nicht erfüllt, also sind die Geraden h und s nicht parallel.
Die Geraden
 sind parallel.
Die Geraden g und h sind parallel.
sind parallel.
Die Geraden g und h sind parallel.
Die Umkehrung des zweiten Strahlensatzes gilt nicht.
Wenn eine Figur wie oben z.B. mit den Maßen
,
,
,
und
angefertigt werden soll, dann ist das Dreieck ABS nicht eindeutig konstruierbar.
Es sind zwar die Seiten b und n sowie der Winkel
gegeben, allerdings ist der Kongruenzsatz SsW nicht erfüllt, da der Winkel
der kürzeren Seite n gegenüber liegt. Damit ist die Eindeutigkeit nicht gegeben.