Steigung linearer Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, welche Bedeutung die Steigung einer linearen Funktion hat, wie du sie am Funktionsgraphen ablesen und wie du sie berechnen kannst.
Bedeutung der Steigung
Die Gleichung einer linearen Funktion hat die Form . In dieser Gleichung beschreibt m die Steigung. Der Wert für m bestimmt, wie sich die Funktionswerte ändern, wenn sich die Argumente ändern. Der zugehörige Graph ist eine Gerade.
f: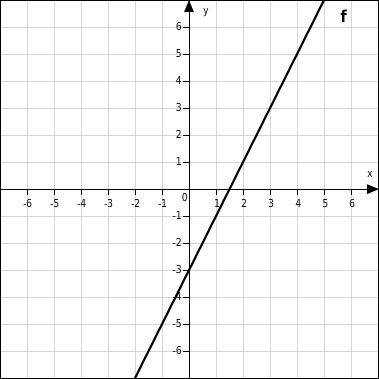 
m = 2Die Steigung ist positiv, das bedeutet, dass die Gerade steigt (von links unten nach rechts oben).Mit größer werdendem x wird der y-Wert größer.Mit kleiner werdendem x wird der y-Wert kleiner.
g: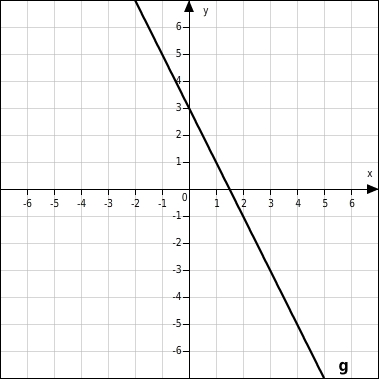 
m = -2Die Steigung ist negativ, das bedeutet, dass die Gerade fällt (von links oben nach rechts unten).Mit größer werdendem x wird der y-Wert kleiner.Mit kleiner werdendem x wird der y-Wert größer.
Betrag der Steigung
Am Betrag der Steigung kannst du erkennen, wie steil der Graph einer lineraen Funktion steigt oder fällt.Je größer der Betrag der Steigung ist, umso steiler steigt oder fällt die Gerade.
f: g: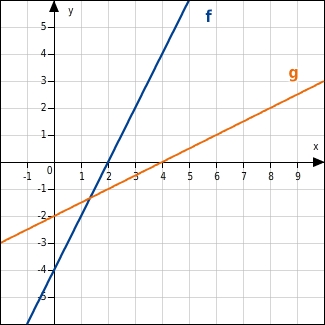 
Die Gerade f steigt steiler als die Gerade g, denn 2 = > =
f: g: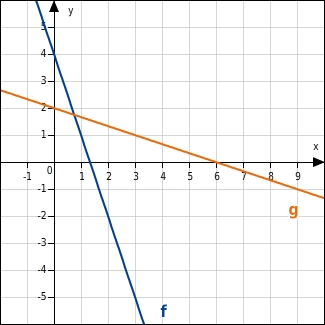 
Die Gerade f fällt steiler als die Gerade g, denn |-3| = | | > | | = | |
Das Steigungsdreieck
Mit dem Steigungsdreieck kannst du die Steigung einer linearen Funktion veranschaulichen. Ein Steigungsdreieck ist rechtwinklig. Am Steigungsdreieck kannst du direkt ablesen, wie sich auf dem Graphen die Koordinaten vom Punkt P zum Punkt Q ändern.
Die Funktion f hat die Steigung 2.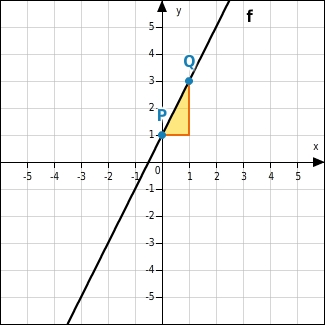 
Um vom Punkt P zum Punkt Q zu gelangen, gehst du eine Einheit nach rechts denn die x-Koordinate ändert sich um +1 und zwei Einheiten nach oben, denn die y-Koordinate ändert sich um +2.
Die Funktion f hat die Steigung -2.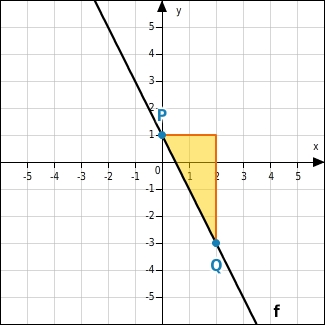 
Um vom Punkt P zum Punkt Q zu gelangen, gehst du zwei Einheiten nach rechts, denn die x-Koordinate ändert sich um +2 und vier Einheiten nach unten, denn die y-Koordinate um -4.
Die änderung der x-Koordinate steht immer im Nenner, die änderung der y-Koordinate im Zähler.
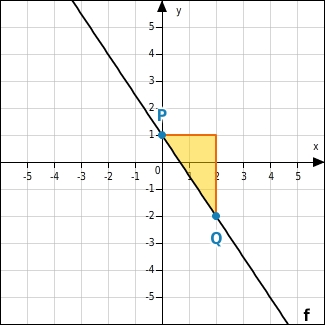
Um vom Punkt P zum Punkt Q zu gelangen, gehst du zwei Einheiten nach rechts, denn die x-Koordinate ändert sich um +2 und drei Einheiten nach unten, denn die y-Koordinate um -3.
Du kannst das Steigungsdreieck auch in die andere Richtung zeichnen.
Funktion g hat die Gleichung .Funktion h hat die Gleichung .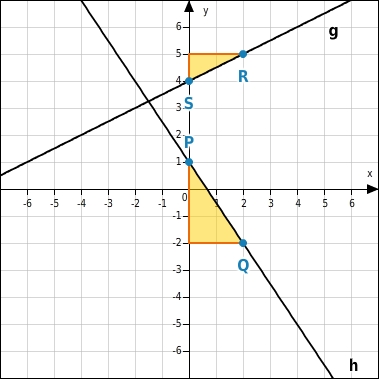 
Funktion g:Vom Punkt R zum Punkt S ändert sich die x-Koordinate um -2, die y-Koordinate um -1.Die Steigung der Funktion ist . Funktion h:Vom Punkt Q zum Punkt P ändert sich die x-Koordinate um -2, die y-Koordinate um +3.Die Steigung der Funktion ist .
Steigung an einer Geraden ablesen
Hast du den Graphen einer linearen Funktion gegeben, kannst du die Steigung bestimmen, indem du ein Steigungsdreieck an der Geraden anlegst.
Bestimme die Steigung der Funktion f.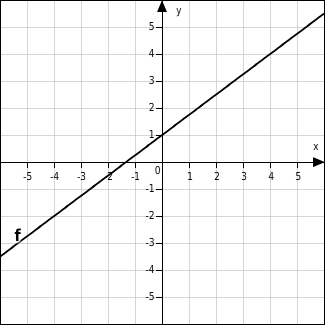 
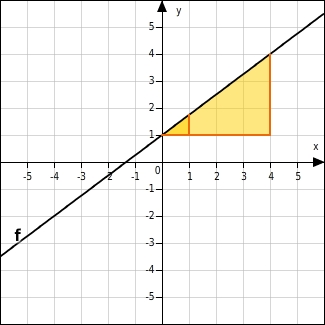
Steigungsdreieck antragen
Du bestimmst die Steigung, indem du von einem beliebigen Punkt der Geraden eine Einheit nach rechts gehst und dann abzählst, wie viele Einheiten du nach oben oder nach unten gehen musst, um wieder zur Geraden zu gelangen.Im Beispiel gelangst du dabei nicht zu einem Punkt mit ganzzahligen Koordinaten. Du kannst also keinen genauen Wert für die Steigung angeben.Daher gehst du mehr als eine Einheit nach rechts, z. B. vier. Anschließend gehst du drei Einheiten nach oben und gelangst zu einem Punkt auf der Geraden mit ganzzahligen Koordinaten. Die Steigung der Geraden und damit der linearen Funktion f ist also .
Gerade mit vorgegebener Steigung zeichnen
Mit Hilfe des Steigungsdreiecks kannst du eine Gerade in ein Koordinatensystem zeichnen.
Gegeben ist die Gerade g und der Schnittpunkt 0 | 3 mit der y-Achse. Verschiebe den orangen Punkt so, dass die Gerade die Steigung hat.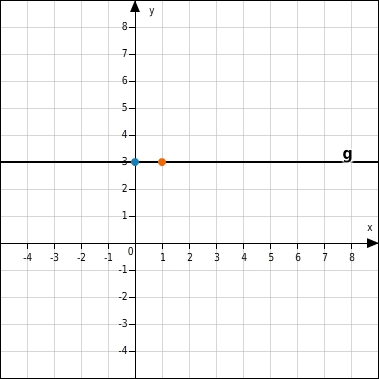 
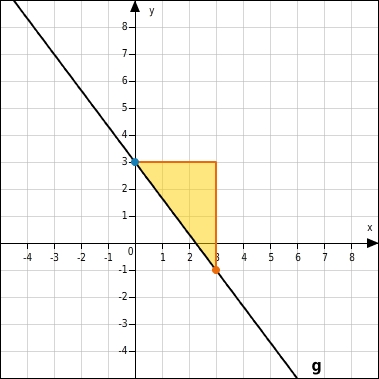
orangen Punkt verschieben
Steigung bedeutet, dass sich die y-Werte um 4 verkleinern, wenn sich die x-Werte um 3 vergrößern.Du nutzt das Steigungsdreieck mit den Seitenlängen 3 und 4 und gehst vom Punkt 0 | 3 aus 3 Einheiten nach rechts und 4 Einheiten nach unten und gelangst zum Punkt (3|-1). Hier lässt du den orangen Punkt los. Es wäre auch ein anderes Steigungsdreieck möglich: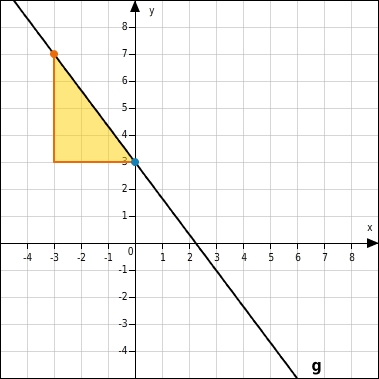 
Verwendest du das negative Vorzeichen für den Nenner, so gehst du 3 Einheiten nach links und 4 Einheiten nach oben.
Bedeutung der Steigung in Sachsituationen
In Sachsituationen, die du mit Hilfe einer linearen Funktion beschreiben kannst, erkennst du die Steigung an Formulierungen wie: •Jede Gesprächsminute kostet . •Das Auto fährt durchschnittlich in einer Stunde. •JederLiter Farbe reicht für Wandfläche. •Die Kartoffeln kosten pro Kilogramm.
Berechnung der Steigung
Hast du von einer Geraden zwei Punkte P ( | ) und Q( | ) gegeben, so kannst du die Steigung der Geraden mit der Steigungsformel berechnen: m = Es wird der Quotient aus den Differenzen der y-Koordinaten und x-Koordinaten der beiden Punkte gebildet. Deshalb wird der rechte Term auch Differenzenquotient genannt.
Die Punkte P( 3 | 4 ) und Q( 5 | 7 ) liegen auf der Geraden g. Berechne die Steigung der Geraden.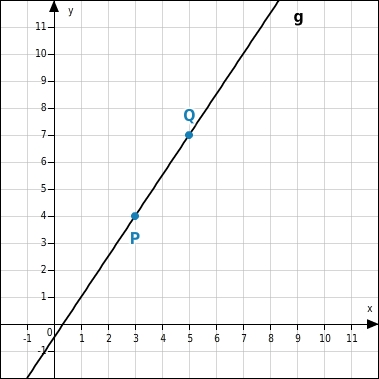 
Koordinaten in die Steigungsformel einsetzen
m =
Steigung berechnen
m =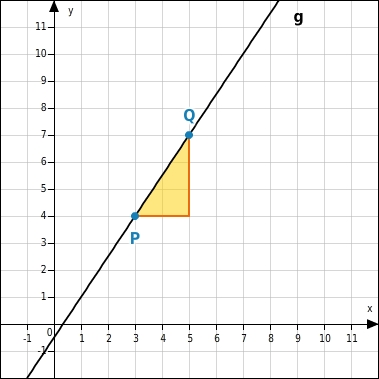 
m =
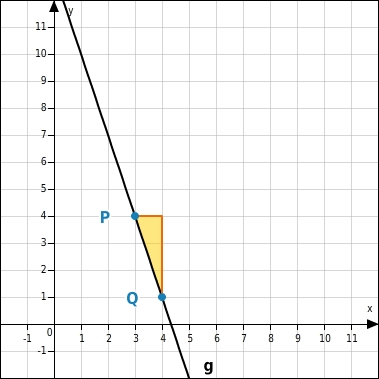
Die Punkte P(
3 | 4
) und Q(
4 | 1
) liegen auf der Geraden g. Berechne die Steigung der Geraden.
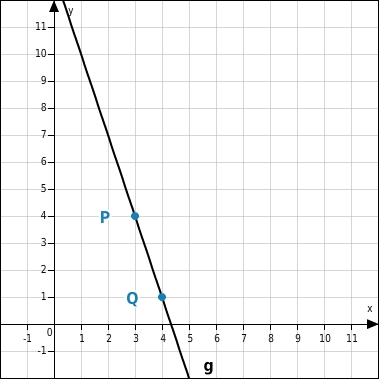
Koordinaten in die Steigungsformel einsetzen
m =
Steigung berechnen
m =
m =
