Funktionsgraphen verstehen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du Funktionsgraphen interpretieren und dadurch nützliche Informationen aus ihnen ablesen kannst.
Aus Funktionsgraphen Wertepaare ablesen
Das ist der Funktionsgraph der Funktion f(x) = .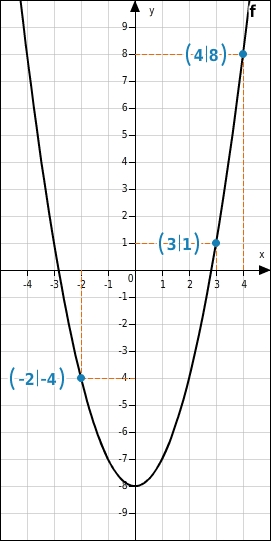 
Der Graph einer Funktion f besteht aus allen Wertepaaren (x;y), wobei x den Definitionsbereich der Funktion durchläuft und stets y = f(x) gilt. Zum Beispiel gehört für das Wertepaar ( ; ) zum Graphen der Funktion f(x) = , denn die Funktion f(x) = ordnet dem Wert den y-Wert y = f( ) = zu. Da Wertepaare (x;y) als Koordinaten von Punkten (x|y) im Koordinatensystem betrachtet werden können, ist es möglich, den Funktionsgraphen wie im obigen Bild zu visualisieren. Die Veranschaulichung des Graphen einer Funktion im Koordinatensystem wird als Funktionsgraph oder einfach Graph (der Funktion) bezeichnet.
Wo liegen die Punkte A( |1), B(0|6), C( | ), D(1|3) und E(2| ) bezüglich des Graphen der Funktion g "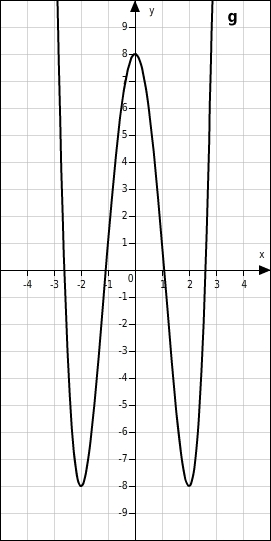 
Die Punkte A( |1) und E(2| ) liegen auf dem Graphen, denn ihre y-Koordinaten sind genauso groß wie die Funktionswerte von g an den zugehörigen Stellen , also = g(-1), und , also = g(2). Die Punkte C( | ) und D(1|3) liegen oberhalb des Graphen, denn ihre y-Koordinaten sind größer als die Funktionswerte von g an den zugehörigen Stellen , also > g( ) = und , also > g(1) = 1. Der Punkt B(0|6) liegt unterhalb des Graphen, denn seine y-Koordinate ist kleiner als der Funktionswert an der zugehörigen Stelle , also < g(0) = 8.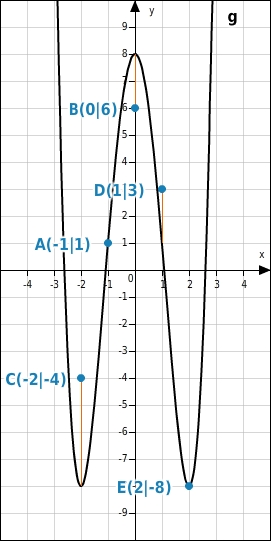 
Vervollständige die Wertetabelle so, dass jedes Wertepaar zum Graphen der Funktion u gehört.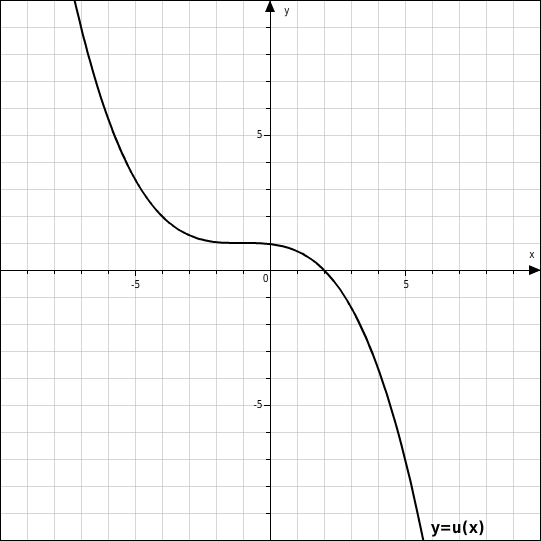 
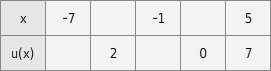
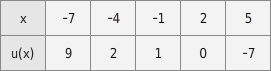
Wertetabelle vervollständigen
Wenn der x-Wert gegeben ist, gehst du wie folgt vor: Du wählst denjenigen Punkt des Graphen, dessen x-Koordinate gleich dem gegebenen x-Wert ist, und liest den zugehörigen y-Wert ab.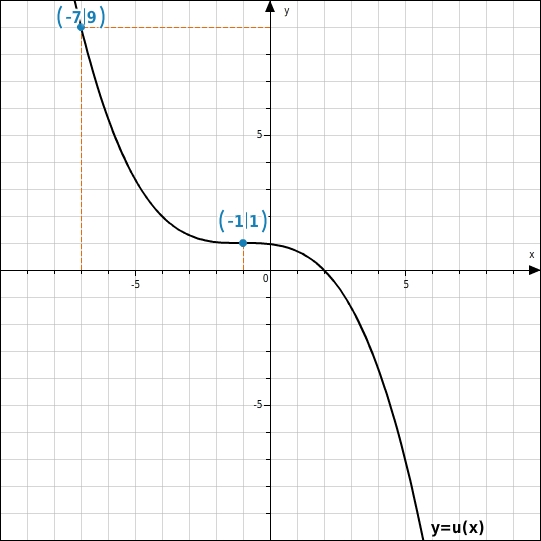 
Wenn der y-Wert gegeben ist, gehst du wie folgt vor: Du wählst denjenigen Punkt des Graphen, dessen y-Koordinate gleich dem gegebenen y-Wert ist, und liest den zugehörigen x-Wert ab.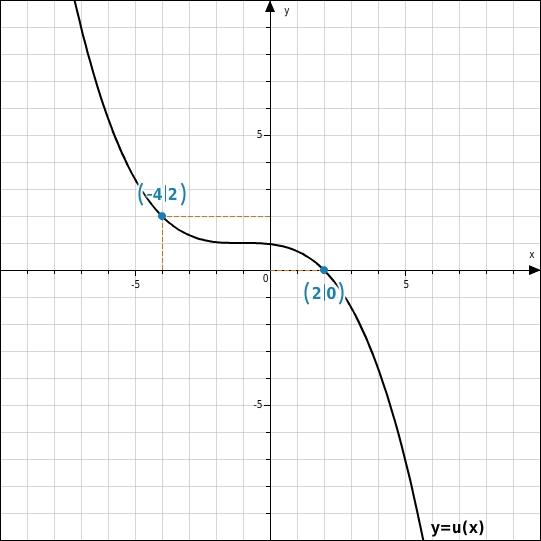 
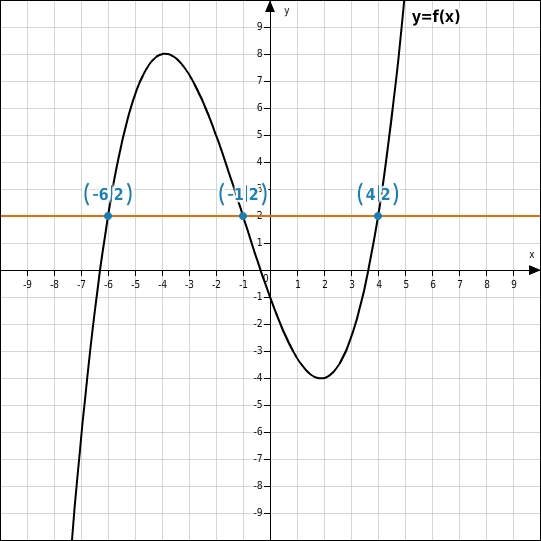
Es gibt drei verschiedene x-Werte, denen der Wert 2 zugeordnet ist.
Bestimme alle x-Werte so, dass die Punkte (x| ) auf dem Graphen der Funktion u liegen.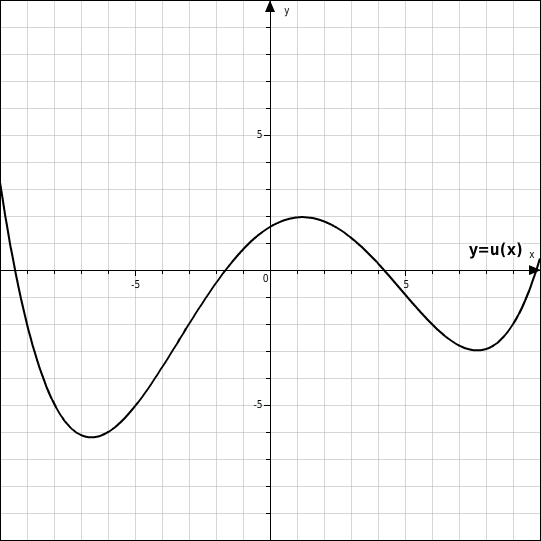 
x-Werte ablesen
Du wählst diejenigen Punkte des Graphen, deren y-Koordinate ist, und liest die zugehörigen x-Werte ab: , , und .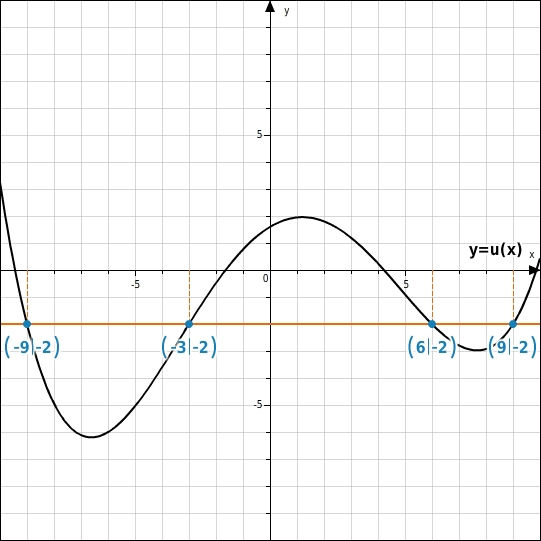 
Die x-Werte sind: -9; -3 ; 6; 9
Definitions- und Wertebereich am Funktionsgraphen erkennen
Hast du eine Funktion nur durch ihren Graphen gegeben, kannst du - zumindest näherungsweise - den Definitionsbereich und den Wertebereich der Funktion ablesen.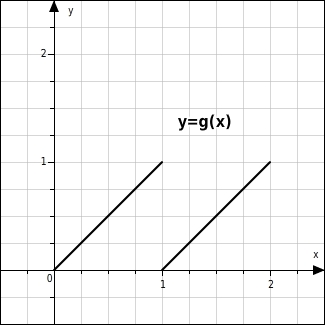 
In der Abbildung ist nicht zu erkennen, ob die Punkte (0|0), (1|1), (1|0) und (2|1) zum Funktionsgraphen gehören und ob der y-Wert 1 überhaupt zugeordnet wird.
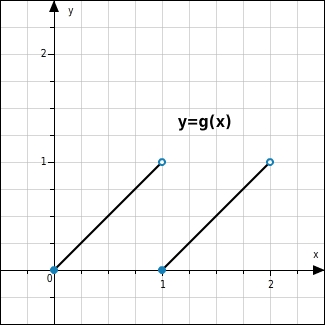
Um beim Zeichnen eines Funktionsgraphen hervorzuheben, dass ein Punkt zum Graphen gehört, wird er mit einem ausgefüllten Kreis markiert. Um beim Zeichnen eines Funktionsgraphen hervorzuheben, dass ein Punkt nicht zum Graphen gehört, wird er mit einem leeren Kreis markiert.
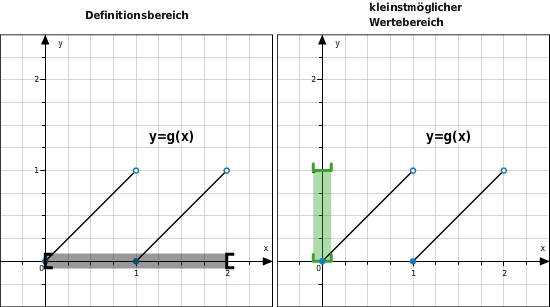
Besondere Punkte auf dem Funktionsgraphen
In vielen Anwendungen der Mathematik geht es um Vorgänge bzw. Zusammenhänge, die mit Hilfe von Funktionen beschrieben werden können. In vielen Fällen spielen dabei besondere Punkte des Graphen eine wichtige Rolle.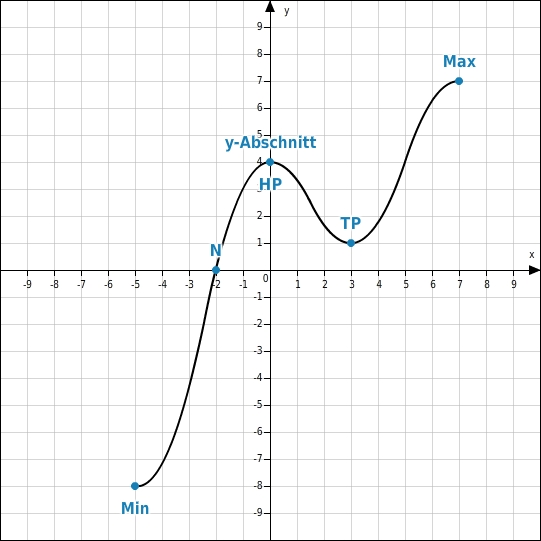 
Das Maximum ist der größte Wert, den eine Funktion annimmt. Die Funktion f nimmt ihren größten Wert im Punkt (7|7) an. Das Minimum ist der kleinste Wert, den eine Funktion annimmt. Die Funktion f nimmt ihren kleinsten Wert im Punkt (-5|-8) an. Beachte, dass es Funktionen gibt, die keinen größten bzw. kleinsten Wert annehmen. Eine Nullstelle ist die x-Koordinate eines Schnittpunktes des Graphen mit der x-Achse. Der Graph der Funktion f schneidet die x-Achse im Punkt (-2|0). Der y-Achsenabschnitt ist die y-Koordinate des Schnittpunktes des Graphen mit der y-Achse. Der Graph der Funktion f schneidet die y-Achse im Punkt (0|4). Ein Hochpunkt ist ein Punkt auf dem Graphen, durch den der Graph hindurch läuft und in dessen Umgebung die Funktionswerte nicht größer sind als der y-Wert am Hochpunkt. Die Funktion f hat einen Hochpunkt bei (0|4). Ein Tiefpunkt ist ein Punkt auf dem Graphen, durch den der Graph hindurch läuft und in dessen Umgebung die Funktionswerte nicht kleiner sind als der y-Wert am Tiefpunkt. Die Funktion f hat einen Tiefpunkt bei (3|1). Beachte, dass die beiden Punkte am Rand des Definitionsbereichs keine Hoch- bzw. Tiefpunkte sind, da man sich diesen Punkten auf dem Graphen jeweils nur von einer Seite nähern kann. Beachte außerdem, dass mehrere besondere Punkte auch zusammenfallen können. Im Beispiel fallen Hochpunkt und y-Achsenabschnitt zusammen.
Monotonie-Intervalle
In vielen Anwendungen ist von Interesse, wie sich die Werte einer Größe ändern, beispielsweise ob sie größer werden oder kleiner. Mit Hilfe sogenannter Monotonie-Intervalle kannst du Bereiche angeben, in denen eine Funktion steigt oder fällt. Oft kann man Monotonie-Intervalle sehr gut - zumindest näherungsweise - am Graphen einer Funktion ablesen.
Im Folgenden Bild sind die Intervalle und die zugehörigen Graphenabschnitte markiert, in denen die Funktion f steigt.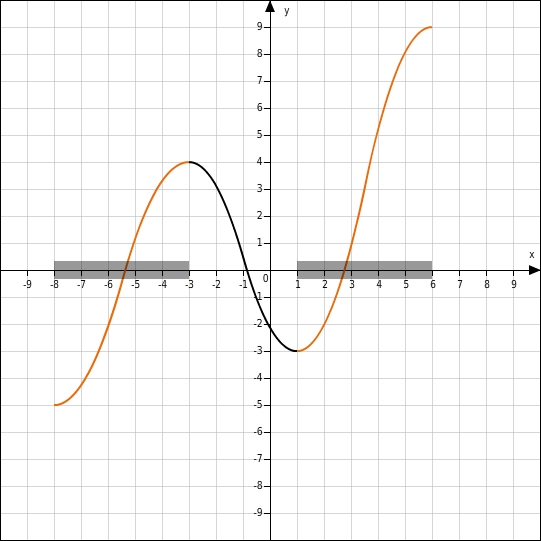 
Die Funktion f steigt also in den Bereichen -8 x -3 und 1 x 6.
Funktionsgraphen und Prozesse
Die Gestalt eines Funktionsgraphen kann Auskunft darüber geben, in welcher Art und Weise ein bestimmter Prozess abläuft.
Ein Gefäß wird bei gleichbleibendem Zufluss mit Wasser gefüllt. Die Füllstandhöhe in Abhängigkeit von der Zeit ist in folgendem Graphen veranschaulicht.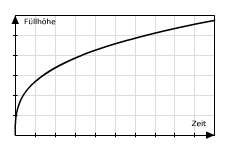 
Zu welchem der drei Gefäße passt der Graph? Am Funktionsgraphen erkennst du, dass zu Beginn des Auffüllens der Wasserstand sehr schnell steigt. Das Gefäß muss also am Boden sehr schmal sein. Somit entfällt das zweite Gefäß, da dieses unten breit ist. Im weiteren Verlauf steigt der Füllstand immer langsamer. Also muss das Gefäß nach oben hin immer breiter werden. Das gesuchte Gefäß ist der auf der Spitze stehende Kegel. 
Graph zuordnen
