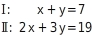Wissen über lineare Gleichungssysteme
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, unter welchen Bedingungen es sinnvoll ist, ein lineares Gleichungssystem zeichnerisch zu lösen und wie du beim rechnerischen Lösen das Additions-, Einsetzungs- oder Gleichsetzungsverfahren geschickt verwenden kannst.
Auswahl eines günstigen Verfahrens zum Lösen eines linearen Gleichungssystems
Jedes lineare Gleichungssystem mit zwei Variablen kannst du zeichnerisch sowie auch rechnerisch mit dem Gleichsetzungs-, dem Einsetzungs- oder dem Additionsverfahren lösen. Manchmal bietet sich ein bestimmtes Verfahren direkt an:
Dieses Verfahren verwendest du, wenn die beiden linearen Gleichungen als zwei Geradengleichungen vorgegeben sind oder sich leicht in solche umformen lassen und wenn dir eine Näherungslösung reicht.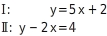
Dieses Verfahren verwendest du, wenn beide Gleichungen auf einer der Seiten bereits einen gleichen Term aufweisen.
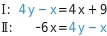Dieses Verfahren verwendest du, wenn eine der Gleichungen auf einer Seite der Gleichung einen Term enthält, der auch in der anderen Gleichung vorkommt.
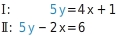Dieses Verfahren verwendest du, wenn in beiden Gleichungen bereits eine Variable mit dem gleichen oder mit der Gegenzahl des Koeffizienten vorkommt, oder wenn du dies auf einfachem Weg erreichen kannst.
Dieses Verfahren verwendest du, wenn beide Gleichungen auf einer der Seiten bereits einen gleichen Term aufweisen.
Dieses Verfahren verwendest du, wenn eine der Gleichungen auf einer Seite der Gleichung einen Term enthält, der auch in der anderen Gleichung vorkommt.
Dieses Verfahren verwendest du, wenn in beiden Gleichungen bereits eine Variable mit dem gleichen oder mit der Gegenzahl des Koeffizienten vorkommt, oder wenn du dies auf einfachem Weg erreichen kannst.
Löse das lineare Gleichungssystem:
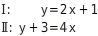Grafisches Lösen eines linearen Gleichungssystems
Du kannst ein lineares Gleichungssystem grafisch lösen, indem du die zwei Gleichungen durch äquivalenzumformung in die Normalform y = m x + n bringst und dann die zugehörigen Geraden in ein Koordinatensystem zeichnest.
Die Lage der Geraden gibt bereits einen überblick über die Lösungen des Gleichungssystems:
L={(2; 5)}
Grafisches Lösen eines linearen Gleichungssystems
Du kannst ein lineares Gleichungssystem grafisch lösen, indem du die zwei Gleichungen durch äquivalenzumformung in die Normalform
Auch wenn es nur eine Lösung gibt, lässt sich diese nicht immer genau ablesen. Wenn du das Gleichungssystem exakt lösen möchtest, verwendest du besser ein rechnerisches Verfahren.
Gleichungssystem grafisch lösen
Gleichung Ⅰ ist bereits in Normalform gegeben. Du stellst Gleichung Ⅱ in die Normalform y = m x + n um: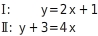 
Jetzt kannst du das lineare Gleichungssystem grafisch lösen, indem du die beiden Geraden in ein Koordinatensystem einzeichnest.
Bei genau einer Lösung des Gleichungssystems (die Geraden haben unterschiedliche Steigungen) kannst du die Werte für die Lösung des linearen Gleichungssystems am Schnittpunkt S(2|5) der Geraden ablesen.
Daraus ergibt sich die Lösungsmenge: L={(2; 5)}.
Die Probe ergibt, dass das Zahlenpaar (2; 5) eine exakte Lösung ist:
Durch Ablesen kannst du aber nicht immer die genaue Lösung ermitteln. Diese erhältst du meist nur durch ein rechnerisches Lösungsverfahren.
Jetzt kannst du das lineare Gleichungssystem grafisch lösen, indem du die beiden Geraden in ein Koordinatensystem einzeichnest.
Bei genau einer Lösung des Gleichungssystems (die Geraden haben unterschiedliche Steigungen) kannst du die Werte für die Lösung des linearen Gleichungssystems am Schnittpunkt S(2|5) der Geraden ablesen.
Daraus ergibt sich die Lösungsmenge: L={(2; 5)}.
Die Probe ergibt, dass das Zahlenpaar (2; 5) eine exakte Lösung ist:
Durch Ablesen kannst du aber nicht immer die genaue Lösung ermitteln. Diese erhältst du meist nur durch ein rechnerisches Lösungsverfahren.
L={(2; 5)}
Lösen mit dem Gleichsetzungsverfahren
Es ist günstig ein lineares Gleichungssystem mit dem Gleichsetzungsverfahren zu lösen, wenn die zwei Gleichungen beide auf einer Seite den gleichen Term aufweisen.
Löse das lineare Gleichungssystem:
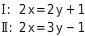
Gleichungssystem lösen
Gleichung Ⅰ und Ⅱ haben beide auf einer Seite den Term
. Du setzt Gleichung Ⅰ und Ⅱ gleich:
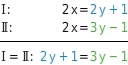Du löst nach
auf:
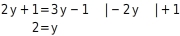Anschließend setzt du den Wert für
in eine der Ausgangsgleichungen ein und erhältst den Wert für
:
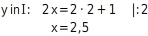
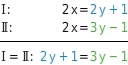Du löst nach
auf:
Anschließend setzt du den Wert für
in eine der Ausgangsgleichungen ein und erhältst den Wert für
:
L={(2; 2,5)}
Lösen mit dem Einsetzungsverfahren
Es ist günstig ein lineares Gleichungssystem mit dem Einsetzungsverfahren zu lösen, wenn eine der Gleichungen auf einer Seite einen Term aufweist, der in der anderen Gleichung ebenfalls als Term vorkommt.
Löse das lineare Gleichungssystem:
Gleichungssystem lösen
Der Term
ist in beiden Gleichungen vorhanden. In Gleichung Ⅰ steht
einzeln auf einer Seite der Gleichung. Du kannst die rechte Seite der Gleichung Ⅰ (
) in Gleichung Ⅱ für
einsetzen:
Du löst nach
auf:
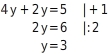Anschließend setzt du den Wert für
in eine der Ausgangsgleichungen ein und erhältst den Wert für
:
Du löst nach
auf:
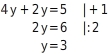Anschließend setzt du den Wert für
in eine der Ausgangsgleichungen ein und erhältst den Wert für
:
L={(1; 3)}
Lösen mit dem Additionsverfahren
Es ist günstig ein lineares Gleichungssystem mit dem Additionsverfahren zu lösen, wenn in beiden Gleichungen bereits eine Variable mit dem gleichen Koeffizienten oder mit dessen Gegenzahl vorkommt.
Löse das lineare Gleichungssystem:
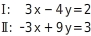
Gleichungssystem lösen
Du addierst die beiden Gleichungen:
Du löst dann nach
auf:
Anschließend setzt du den Wert für
in eine der Ausgangsgleichungen ein und erhältst den Wert für
:
Du löst dann nach
auf:
Anschließend setzt du den Wert für
in eine der Ausgangsgleichungen ein und erhältst den Wert für
:
L={(2; 1)}
Knobelaufgaben zu linearen Gleichungssystemen
Ein lineares Gleichungssystem kannst du auch selbst aufstellen und bestimmen, ob es keine, eine oder unendlich viele Lösungen haben soll.
In Knobelaufgaben zu linearen Gleichungssystemen wird manchmal gefordert, als Lückenaufgabe ein Gleichungssystem zu vervollständigen, das eine bestimmte Anzahl von Lösungen besitzen soll.
Lückenaufgabe - lineares Gleichungssystem hat keine Lösung
Bestimme den Koeffizienten von
so, dass das lineare Gleichungssystem keine Lösung hat.
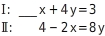
Koeffizient bestimmen
Das lineare Gleichungssystem hat keine Lösung, wenn nach Anwendung des Lösungsverfahrens eine falsche Aussage entsteht.
In dieser Aufgabe fehlt der Koeffizient von
. Um das Additionsverfahren anwenden zu können, stellst du die Gleichung Ⅱ so um, dass die Summanden mit gleichen Variablen untereinander stehen.
Du multiplizierst Gleichung Ⅰ mit 2, damit der Koeffizient von
in Gleichung Ⅰ (8) die Gegenzahl des Koeffizienten von
in der umgestellten Gleichung Ⅱ (-8) ist:
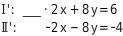Um eine falsche Aussage zu erhalten, müssen die Summanden mit den Variablen
und
bei Addition der Gleichungen wegfallen. Dies ist der Fall, wenn auch der Koeffizient von
in Gleichung Ⅰ' die Gegenzahl des Koeffizienten von
in Gleichung Ⅱ' (-2) ist. Die Gegenzahl ist 2. Die gesuchte Zahl ist also 1, da
=
.
Um eine falsche Aussage zu erhalten, müssen die Summanden mit den Variablen
und
bei Addition der Gleichungen wegfallen. Dies ist der Fall, wenn auch der Koeffizient von
in Gleichung Ⅰ' die Gegenzahl des Koeffizienten von
in Gleichung Ⅱ' (-2) ist. Die Gegenzahl ist 2. Die gesuchte Zahl ist also 1, da
=
.
Lückenaufgabe - lineares Gleichungssystem hat unendlich viele Lösungen
Bestimme die Koeffizienten von
und
so, dass das lineare Gleichungssystem unendlich viele Lösungen hat.
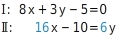
Koeffizienten bestimmen
Das lineare Gleichungssystem hat unendlich viele Lösungen, wenn nach Anwendung eines Lösungsverfahrens eine wahre Aussage (beispielsweise
=
) entsteht.
Hier fehlen die Koeffizienten von
und
. Um das Additionsverfahren anwenden zu können, stellst du die Gleichung Ⅱ so um, dass die Summanden mit gleichen Variablen untereinander stehen:
Die Zahlen ohne Variable müssen Gegenzahlen voneinander sein, damit bei einer Addition der Gleichungen die rechte Seite der Gleichung
ergibt. Du multiplizierst Gleichung Ⅰ mit -2:
Es entsteht nach Addition eine wahre Aussage, wenn jeweils die Koeffizienten von
in den Gleichungen Gegenzahlen (-16 und 16) und die Koeffizienten von
in den Gleichungen Gegenzahlen (-6 und 6) sind.
Dies ist für die Zahlen 16 und 6 erfüllt:
Die Zahlen ohne Variable müssen Gegenzahlen voneinander sein, damit bei einer Addition der Gleichungen die rechte Seite der Gleichung
ergibt. Du multiplizierst Gleichung Ⅰ mit -2:
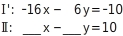Es entsteht nach Addition eine wahre Aussage, wenn jeweils die Koeffizienten von
in den Gleichungen Gegenzahlen (-16 und 16) und die Koeffizienten von
in den Gleichungen Gegenzahlen (-6 und 6) sind.
Dies ist für die Zahlen 16 und 6 erfüllt:
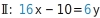
Lineares Gleichungssystem erstellen - eine Lösung
Gib ein Gleichungssystem bestehend aus zwei linearen Gleichungen mit je zwei Variablen an. Wähle die Gleichungen so, dass das Gleichungssystem die Lösungsmenge L={(2;5)} hat.
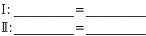
Gleichungssystem aufstellen
Es gibt viele lineare Gleichungssysteme, die die Lösungsmenge L={(2;5)} haben. Du kannst die Gleichungen erstellen, indem du zunächst die gegebenen Zahlen addierst:
Für eine zweite Gleichung, die nicht genauso aussieht, wie die erste, kannst du einfach beliebige Faktoren vor die Lösungen 2 und 5 setzen und das Endergebnis errechnen:
Das folgende Gleichungssystem hat also die vorgegebene Lösungsmenge L={(2;5)}:
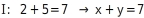Für eine zweite Gleichung, die nicht genauso aussieht, wie die erste, kannst du einfach beliebige Faktoren vor die Lösungen 2 und 5 setzen und das Endergebnis errechnen:
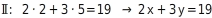Das folgende Gleichungssystem hat also die vorgegebene Lösungsmenge L={(2;5)}:
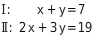
Eine mögliche Lösung ist:
