Wissen über lineare Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du dein Wissen über lineare Funktionen geschickt nutzen kannst, um den Wahrheitsgehalt von Aussagen zu überprüfen oder um Punkte unter bestimmten Bedingungen im Koordinatensystem zu finden.
Schnittpunkte mit den Koordinatenachsen
Der Graph einer linearen Funktion f mit der Funktionsgleichung (und uneingeschränktem Definitionsbereich) schneidet die y-Achse im Punkt . Einen Schnittpunkt x 0 | 0 mit der x-Achse gibt es dann, wenn m≠0. Für ist der Graph eine Gerade parallel zur x-Achse. 
Eine Gerade, die parallel zu y-Achse verläuft, ist kein Funktionsgraph. Zu einem x-Wert gehören in diesem Fall mehrere y-Werte.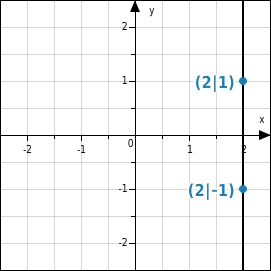 
Ist die Steigung der Geraden -1 und b ungleich 0, dann schneidet die Gerade die Koordinatenachsen so, dass ein gleichschenkliges Dreieck entsteht, der y-Achsenabschnitt und die Nullstelle haben den gleichen Wert.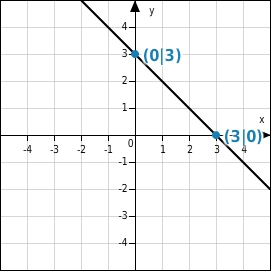 
In diesem Fall ist dann und
Die Schnittpunkte mit den Koordinatenachsen kannst du mit Hilfe der Parameter in der Geradengleichung in Normalform schnell bestimmen. Den y-Achsenabschnitt kannst du direkt ablesen, die Gerade schneidet die y-Achse im Punkt (0|b). Die Nullstelle berechnest du, indem du für y den Wert 0 einsetzt und die Gleichung nach x auflöst. Die Gerade schneidet die x-Achse im Punkt ( | )
Die Gerade g mit der Gleichung schneidet die y-Achse im Punkt ( | ) und die x-Achse im Punkt ( | ). Ist der y-Achsenabschnitt , so nennt man die Gerade Ursprungsgerade. 
Steigung
Der Graph einer linearen Funktion ist eine Gerade. Die Gerade verläuft je nach Steigung 
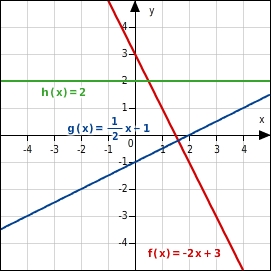
Die Funktionen, deren Graphen die Steigung Null haben, heißen konstante Funktionen. Alle Punkte auf dem Graphen der konstanten Funktion haben dieselbe y-Koordinate. Ist die Steigung größer als Null, steigt die Gerade. Ist die Steigung kleiner als Null, fällt die Gerade. Dabei beziehen sich die Begriffe „steigen“ und „fallen“ darauf, dass man den Verlauf der Geraden gewissermaßen „von links nach rechts“ betrachtet.
Die Steigung kannst du der Geradengleichung in Normalform ( ) direkt entnehmen. Sie ist gleich m, also der Koeffizient von x. Sind die Steigungen zweier Gerade gleich und ihre y-Abschnitte verschieden, dann sind die Geraden parallel. 
Ja nach Skalierung der Koordinatenachsen kann der Graph einer linearen Funktion steiler oder flacher erscheinen.
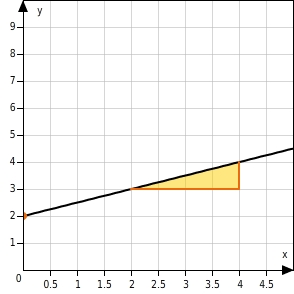
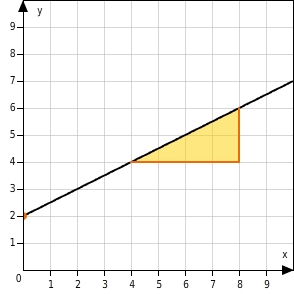
Beide Graphen gehören zur gleichen linearen Funktion f mit . Beide Geraden schneiden die y-Achse an der Stelle . Durch die unterschiedliche Skalierung der Koordinatenachsen verlaufen die Geraden unterschiedlich steil. An den Steigungsdreiecken kannst du aber sehen, dass beide Geraden dieselbe Steigung haben.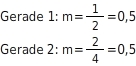 
Du kannst durch die Skalierung der Koordinatenachsen bewirken, dass die Graphen von zwei verschiedenen linearen Funktionen gleich aussehen.
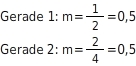
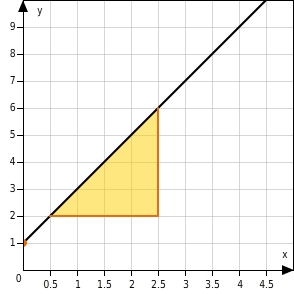
Beide Graphen gehören zu verschiedenen linearen Funktion f und g mit und Beide Geraden schneiden die y-Achse an der Stelle . An den Steigungsdreiecken kannst du sehen, dass beide Geraden verschiedene Steigungen haben. 
Durch die unterschiedliche Skalierung der Koordinatenachsen erscheinen die Geraden aber parallel.
