Volumen- und Oberflächenberechnung
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenEigenschaften von Kugeln
Die Kugel ist ein geometrischer Körper der entsteht, wenn ein Kreis (oder ein Halbkreis) um seinen Durchmesser rotiert. Alle Punkte auf der Kugeloberfläche haben denselben Abstand r (Radius) vom Mittelpunkt M der Kugel.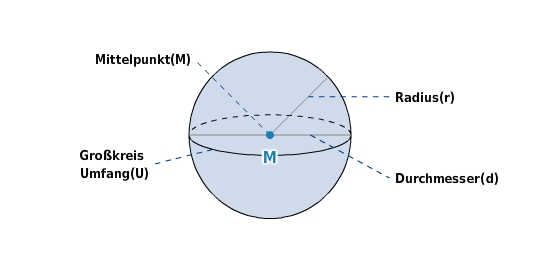 
Volumenberechnung
Faustformel: Da ≈ , heben sich der Nenner 3 und bei einer überschlagsrechnung gegeneinander auf.
Kugel mit einem Radius r von 
Beim Runden auf ganze Hunderter ergibt sich in beiden Fällen das gleiche Ergebnis.
Mit der Formel zur Berechnung des Volumens kannst du auch den Radius der Kugel berechnen.Du stellst die Formel mit Hilfe von äquivalenzumformungen nach dem Radius um: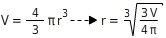 
Oberflächenberechnung
Kugel mit einem Radius r von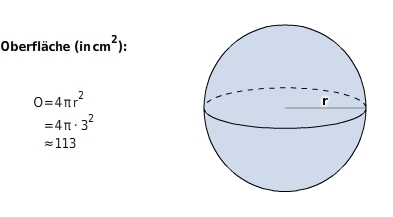 
Mit der Formel zur Berechnung der Oberfläche kannst du auch den Radius der Kugel berechnen.Du stellst die Formel mit Hilfe von äquivalenzumformungen nach dem Radius um: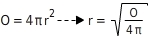 
Kugelabschnitte
Das Volumen eines Kugelabschnitts oder -keils entspricht dem Anteil, den dieser an der Kugel hat. Die Oberfläche eines Kugelabschnitts oder -keils setzt sich zusammen aus: 
Eine Achtelkugel ist begrenzt von einem Achtel der Oberfläche und drei Viertelkreisen:Es ergibt sich:
Berechnungen an zusammengesetzten Körpern
Ein zusammengesetzter Körper besteht aus zwei oder mehr Teilkörpern.Das Volumen des zusammengesetzten Körpers ist die Summe der Volumen aller Teilkörper.Die Oberfläche ist die aller begrenzenden Teilflächen.
Beachte, dass die Flächen, an denen sich die Körper berühren, nicht zur Oberfläche gehören.
Du gehst Schritt für Schritt vor: 
Volumenberechnung (Maße in m)
1.Teilkörper: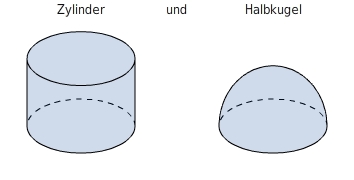
2. Formeln:
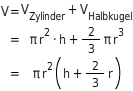
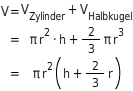
Rundungsfehler beim Rechnen bleiben klein, wenn du zuerst zusammenfasst und möglichst spät, bzw. erst am Ende mit .
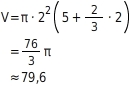
Berechnungen an ausgehöhlten Körpern
Ein ausgehöhlter Körper entsteht, indem du aus einem Körper einen oder mehrere andere Körper herausschneidest. Das Volumen des ausgehöhlten Körpers ist also kleiner als das des Grundkörpers ( ). Die Oberfläche ist die aller begrenzenden Teilflächen. Sie kann größer werden. Du gehst Schritt für Schritt vor. 
Oberflächenberechnung (Maße in cm)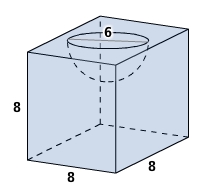
1. Teilfläche:
Die Fläche des aus einer Würfelseite herausgeschnittenen Kreises entspricht der Schnittfläche der Halbkugel und wird subtrahiert.
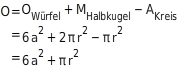
Die Kugel als Rotationskörper
Wird eine Kugel entlang der Ebene, in der eine ihrer Symmetrieachse liegt, geschnitten, so entsteht als Axialschnitt der Kugel ein Kreis. Rotiert ein Kreis um seinen Durchmesser, so entsteht als Rotationskörper eine Kugel. Rotiert ein Halbkreis um die , so entsteht als Rotationskörper eine Halbkugel.
Funktionale Abhängigkeiten
Volumen und Oberfläche der Kugel hängen ausschließlich vom Radius der Kugel ab.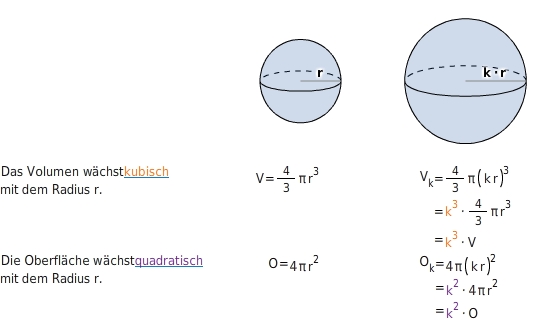 
Wird also der Radius verdoppelt, dann verachtfacht sich das Volumen und vervierfacht sich die Oberfläche.
