Scheitelpunktform: Parabeln verschieben, strecken und stauchen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenVerschiebung entlang der y-Achse
Addierst du zum Funktionsterm der Funktion f mit f(x)=x2 eine Konstante e, dann ist der Graph der neuen Funktion g(x)=x2+e eine entlang der y-Achse verschobene Normalparabel. Der Scheitelpunkt dieser Parabel ist S(0|e) .
Für e>0 wird die Parabel entlang der y-Achse um e Einheiten nach oben verschoben. Für e<0 wird die Parabel entlang der y-Achse um e Einheiten nach unten verschoben.
y=x2+3 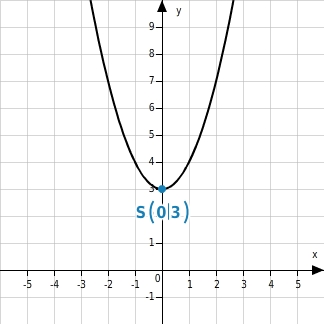

y=x2-2 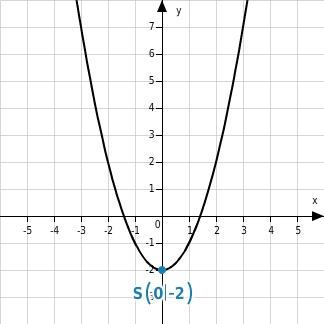

Verschiebung entlang der x-Achse
Subtrahierst du von den Argumenten der Funktion f mit f(x)=x2 eine Konstante d, dann ist der Graph der neuen Funktion g(x)=(x-d)2 eine entlang der x-Achse verschobene Normalparabel. Der Scheitelpunkt dieser Parabel ist S(d|0) .
Für d>0 ist die Parabel entlang der x-Achse um d Einheiten nach rechts verschoben. Für d<0 ist die Parabel entlang der x-Achse um d Einheiten nach links verschoben.
y=(x-2)2 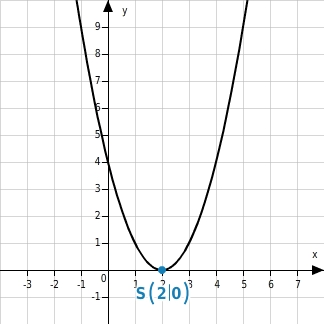

y=(x-(-2))2 = (x+2)2 

Streckung, Stauchung und öffnung
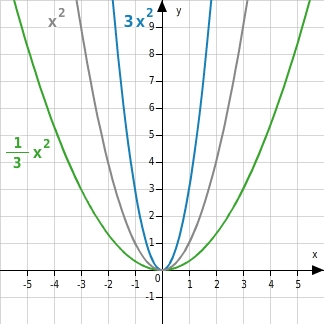
Multiplizierst du den Funktionsterm f(x)=x2 mit einem konstanten Faktor a, so verändert sich die Form bzw. die öffnung der zugehörigen Parabel. Es entsteht der Graph der Funktion g mit g(x)=ax2 . Der Faktor a wird auch Streckfaktor genannt. Der Scheitelpunkt dieser Parabel liegt im Punkt S(0|0) .
Für a>0 ist die Parabel nach oben geöffnet. Sie besitzt einen Tiefpunkt. Für a<0 ist die Parabel nach unten geöffnet. Sie besitzt einen Hochpunkt.

Für 0<|a|<1 ist die Parabel „breiter“ als die Normalparabel. Sie ist also in y-Richtung gestaucht. Für |a|>1 ist die Parabel „schmaler“ als die Normalparabel. Sie ist also in y-Richtung gestreckt. Für a=1 ist es die Normalparabel.
Scheitelpunktform
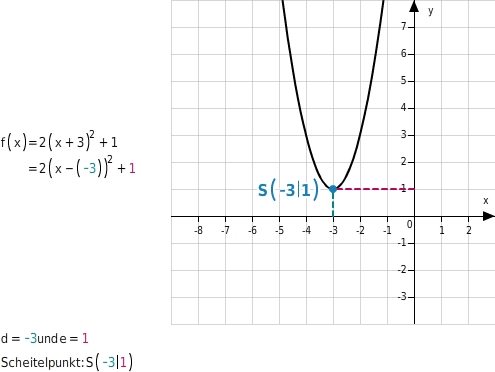
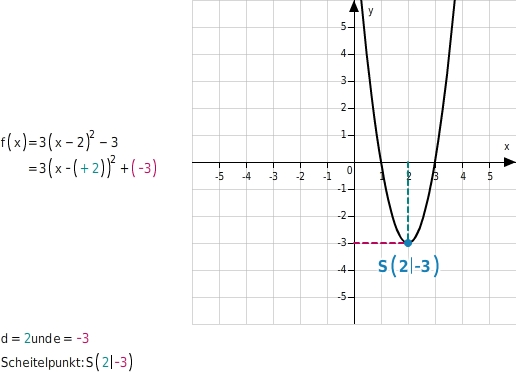
Oft werden quadratische Funktionsterme in der Scheitelpunktform angegeben: f(x)=a(x-d)2+e Du kannst aus ihr die Koordinaten des Scheitelpunkts der zugehörigen Parabel direkt ablesen: S(d|e) Zusätzlich kannst du den Streckfaktor a der Parabel ablesen. Es ist der Faktor vor der Klammer.