Quartile und Boxplots
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, was Quartile und Boxplots sind, wie du Quartile ermittelst und welche Rolle sie bei Boxplots spielen.
Quartile
Quartil ist lateinisch und heißt wörtlich übersetzt . Quartile zerlegen eine sortierte von Beobachtungen in vier (annähernd) gleich große Abschnitte oder .
Das erste Quartil wird auch unteres Quartil genannt (abgekürzt ). Das dritte Quartil wird auch oberes Quartil genannt (abgekürzt ). Der M ist der Wert in der Mitte oder das der beiden mittleren Werte. Er wird manchmal auch zweites Quartil genannt.
Charakterisierende :Höchstens ein Viertel der Beobachtungen ist kleiner als und höchstens drei Viertel der Beobachtungen sind größer als . Charakterisierende :Höchstens drei Viertel der Beobachtungen sind kleiner als und höchstens ein Viertel der Beobachtungen ist größer als .
Bestimmung der Quartile
Um die Quartile zu bestimmen, sortierst du die Beobachtungswerte der Größe nach mit dem kleinsten Wert beginnend. Ist der Umfang N der gerade, so teilt der Median die Datenreihe in zwei gleich große . Die Quartile sind jeweils die Mediane der Datenhälften.
Ist der Umfang N der Datenreihe ungerade, so ist der Median der Wert in der Mitte. Enthalten auch die verbleibenden Datenhälften eine ungerade Anzahl von Datenwerten, nimmst du als erstes oder drittes Quartil wieder jeweils davon den Median, also den Wert in der Mitte.
Für den Fall, dass die beiden verbleibenden Datenhälften jeweils eine gerade Anzahl von Datenwerten enthalten, gibt es keine einheitliche Regel: Nach unserer Regel ist das erste Quartil der Datenwert nach dem Median der unteren Datenhälfte und das dritte Quartil der Datenwert vor dem Median der oberen Datenhälfte. Es gibt auch die vereinfachte Regel, bei der der Median der jeweiligen Datenhälfte genommen wird. Bei großen Datenreihen spielt dieser Unterschied aber keine Rolle.
Boxplots
Mit einem Boxplot kannst du die Verteilung der Beobachtungen einer graphisch darstellen.Er ist eine Zusammenfassung der fünf einer Beobachtungsreihe und besteht aus dem
Als Eselsbrücke kannst du dir die Boxplot-Buchstabenfolge merken:M - Q - M - Q - M(Minimum - Quartil - Median - Quartil - Maximum) Bestandteile eines Boxplots:Der Boxplot besteht aus der Box, sowie der linken und der rechten Antenne. In der Box markiert ein senkrechter Strich den . Die linke Kante der Box liegt auf dem ersten, die rechte auf dem dritten .Das Ende der linken Antenne markiert das . Das Ende der rechten Antenne markiert das .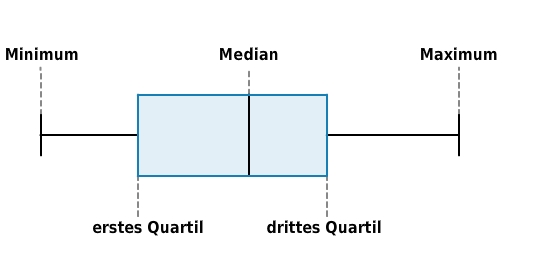 
Die Boxplot-Buchstaben: M - Q - M - Q - M (Minimum - Quartil - Median - Quartil - Maximum)
Ein Boxplot stellt übersichtlich die in Quartile zerlegte Verteilung der Beobachtungen um den Median herum dar: Etwa der Daten liegen innerhalb der Box, etwa links von der Box, etwa rechts von der Box. Die Breite der Box zeigt an, ob die mittlere Hälfte der Daten eher nahe dem Median oder weiter verstreut davon liegen. Je kleiner die Box, desto mehr konzentriert sich die mittlere Hälfte der Daten um den Median. Die Lage des Median in der Box zeigt an, ob sich die mittlere Hälfte der Daten auf einer Seite des Median konzentrieren. Je kürzer eine Seite der Box im Vergleich zur anderen Seite ist, desto mehr konzentriert sich die mittlere Hälfte auf dieser Seite des Median.
