Prisma
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenEigenschaften von Prismen
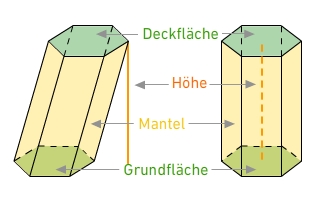
Ein Prisma (manchmal auch Säule genannt) ist ein geometrischer Körper mit
kongruentenund parallelen
n-Eckenals Grund- und Deckfläche.
Die Mantelfläche besteht aus n
Parallelogrammen.
Beim geraden Prisma besteht die Mantelfläche aus n
Rechtecken.
Beachte, auch Rechtecke sind Parallelogramme.
schiefes Prismagerades Prisma
Im Weiteren wird das gerade Prisma kurz als Prisma bezeichnet. Ist von einem schiefen Prisma die Rede, so wird das ausdrücklich erwähnt.
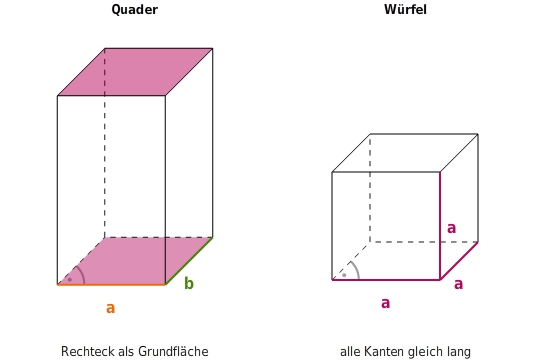
Spezialfälle gerader Prismen:
Volumenberechnung
Volumen=Grundfläche·Höhe
kurz:
V=G·h
Je nach Grundfläche des Prismas ergeben sich dann speziellere Formeln.
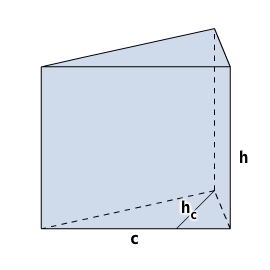
Prisma mit Dreieck ABC als Grundfläche (
hc=16cm,
c=42cm) und einer Höhe h von
84cm
Grundfläche G (incm2):
Volumen V (incm3):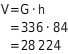
Grundfläche G (incm2):
Volumen V (incm3):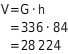
Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen eines Prismas berechnen.
Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
V=G·h
h=VGund
G=Vh
h=VGund
G=VhOberflächenberechnung
Oberfläche=2·Grundfläche+Mantelfläche
kurz:
O=2G+M
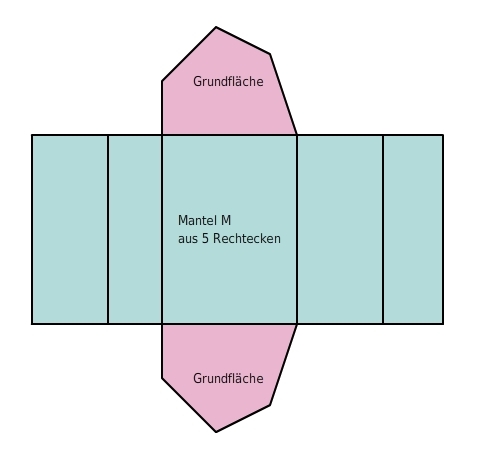Die Oberfläche eines Prismas setzt sich zusammen aus zwei Grundflächen G und der Mantelfläche M.
O=2G+M
Die Grundfläche ist ein
n-Eckmit dem Umfang U.
Der Mantel ist ein
Rechteckmit den Seitenlängen U (Umfang der Grundfläche) und h (Höhe des Prismas).
M=U·hJe nach Grundfläche des Prismas ergeben sich dann speziellere Formeln.
Prisma mit einem rechtwinkligen Dreieck ABC als Grundfläche (
a=3m,
b=4m,
c=5m) und einer Höhe h von
8.5m
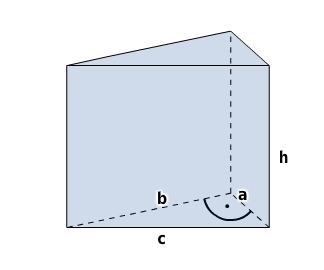Grundfläche (inm2):
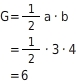Mantelfläche (drei Rechtecke) (inm2):
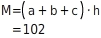Oberflächeninhalt (inm2):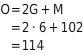
Grundfläche (inm2):
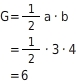Mantelfläche (drei Rechtecke) (inm2):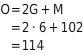
Oberflächeninhalt (inm2):
Mit der Formel zur Berechnung des Oberflächeninhalts kannst du auch die anderen Größen eines Prismas berechnen.
Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
O=2G+M
M=O-2Gund
G=O-M2
M=O-2Gund
G=O-M2Funktionale Abhängigkeiten
Bei gleichbleibender Grundfläche G wächst das Volumen V
linearzur Höhe h.
D. h., wird die Höhe mit einem Faktor (k) vervielfacht, vervielfacht sich das Volumen mit demselben Faktor (k).
Bei gleichbleibender Höhe, wächst das Volumen V auch zur Grundfläche G proportional.
Bei gleichbleibender Grundfläche G wächst die Mantelfläche M proportional zur Höhe h.
D. h., wird die Höhe mit einem Faktor (k) vervielfacht, vervielfacht sich die Mantelfläche mit demselben Faktor (k).
Die Mantelfläche ist ein Rechteck.
Für die Berechnung von Grund- und Deckfläche spielt die Höhe eines Prismas keine Rolle.
Die Oberfläche wächst deshalb nicht proportional zur Höhe. Sie wächst aber linear mit der Höhe.
