Primzahlen kennenlernen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, was Primzahlen sind.
Primzahlen
Eine natürliche Zahl größer als 1 ist eine Primzahl, wenn sie nur durch sich selbst und durch 1 teilbar ist. Das bedeutet, eine natürliche Zahl ist eine Primzahl, wenn sie genau zwei Teiler besitzt.
Der griechische Mathematiker Euklid (um 340 v. Chr. bis um 270 v. Chr.) hat bewiesen, dass es unendlich viele Primzahlen gibt.
Primzahl: Eine natürliche Zahl heißt Primzahl, wenn sie genau zwei verschiedene Teiler besitzt: Sie ist durch 1 und durch sich selbst teilbar.
Die Primzahlen bis 100
Die Primzahlen bis 100 solltest du auswendig können.
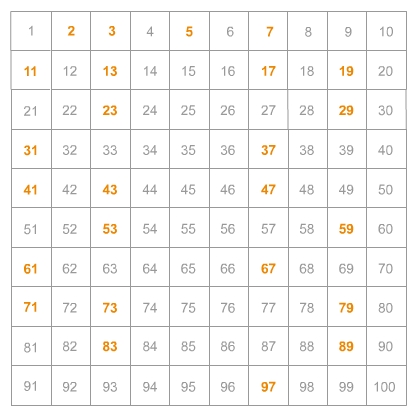Die Primzahlen sind hier gefärbt.
Primzahlen finden
Um alle Primzahlen bis zu einer festen natürlichen Zahl zu bestimmen, gibt es ein einfaches Verfahren, das von dem griechischen Mathematiker Eratosthenes (um 276 v. Chr. Bis um 194 v. Chr.) stammt.
Es wird als Sieb des Eratosthenes bezeichnet.
Das Sieb des Eratosthenes
Finde alle Primzahlen, die kleiner als 100 sind.
Primzahlen finden
Wissenswertes über Primzahlen
Manche Primzahlen haben besondere Eigenschaften.
Primzahlzwillinge
Wenn zwei Primzahlen den Abstand 2 haben, nennt man sie Primzahlzwillinge. Ob es unendlich viele Paare von Primzahlzwillingen gibt, ist bis heute nicht bekannt.
Beispiele hierfür kannst du in der Primzahltabelle ablesen:
- 3 und 5
- 5 und 7
- 11 und 13
- 17 und 19
Da die Primzahlzwillinge immer ungerade sind, liegt zwischen ihnen genau eine gerade Zahl.
Die Zahl zwischen den Primzahlzwillingen (außer bei 3 und 5) ist durch 3 teilbar, da jede dritte Zahl durch 3 teilbar ist und die Primzahlen größer 3 nicht durch 3 teilbar sind.
Das bedeutet, dass zwischen jedem Zwillingspaar außer dem ersten immer eine durch 6 teilbare Zahl liegt.
Summe zweier Primzahlen
Die Summe zweier Primzahlen (ohne die 2) ist als Summe ungerader Zahlen immer gerade.
Es scheint, dass umgekehrt auch jede gerade Zahl größer als 2 die Summe zweier Primzahlen ist.
...
Dies hat der deutsche Mathematiker und Diplomat Christian von Goldbach 1742 durch Probieren bei kleinen geraden Zahlen festgestellt. Ob er aber tatsächlich recht hat, ist bis heute nicht bekannt.
Das Doppelte einer natürlichen Zahl
Zwischen jeder natürlichen Zahl größer als 1 und ihrem Doppelten liegt mindestens eine Primzahl.
Das hat 1845 der französische Mathematiker Joseph Louis Fran?ois Bertrand behauptet. Es wurde 1850 von dem russischen Mathematiker Pafnuti Lwowitsch Tschebyschew bestätigt.
Primzahlen als Summe von Quadratzahlen
Genau die Primzahlen, die bei Division durch 4 den Rest 1 haben, lassen sich als Summe von zwei Quadratzahlen schreiben.
R 1
Dies war bereits Pierre de Fermat bekannt (1607 - 1665), wurde aber erst 1749 von Leonhard Euler(1707 - 1783) bewiesen.
Ist der Rest 3, so lässt sich die Primzahl sogar als Summe von 3 oder 4 Quadratzahlen schreiben.
