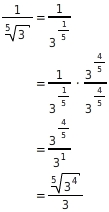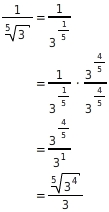Potenzgesetze für Potenzen mit rationalem Exponenten
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenPotenzen mit rationalen Exponenten
Für eine positive reelle Zahl a und natürliche Zahlen
,
wird vereinbart:
und
Für positive Exponenten darf auch
sein:
Du kannst jede
mit rationalem
und jede Potenz mit rationalem Exponenten als Wurzel schreiben.
Insbesondere lassen sich damit
als Potenzen mit rationalen Exponenten schreiben.
Potenzgesetze
Potenzen mit gleicher Basis
Für rationale Zahlen r und s und eine positive reelle Zahl a gilt:
und
Für positive Exponenten darf beim Multiplizieren auch
sein:
Die Division durch 0 ist jedoch nicht möglich.
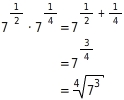
Potenzen mit gleichem Exponenten
Für eine rationale Zahl r und positive reelle Zahlen a und b gilt:
und
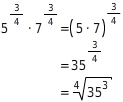
Potenzen von Potenzen
Für rationale Zahlen r und s und eine positive reelle Zahl a gilt:

Berechnen von Potenzen mit rationalem Exponenten
Auf Grund der
ist es bei der Berechnung einer Potenz mit rationalem Exponenten egal, ob du erst
und dann die
oder umgekehrt.
Für eine positive reelle Zahl a und natürliche Zahlen
,
gilt:
ist die 3. Wurzel aus der 2. Potenz von 8.
oder
ist die 2. Potenz der 3. Wurzel aus 8.
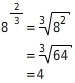 oder
oder 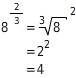
Auch bei negativen Exponenten gibt es entsprechende Formulierungen.
Für eine positive reelle Zahl a und natürliche Zahlen
,
gilt:
Rechnen mit Wurzeln
Mit Hilfe der
lassen sich auch die Rechenregeln für
herleiten.
Du schreibst die Wurzeln als Potenzen und wendest das Potenzgesetz für Potenzen mit gleicher Basis an.
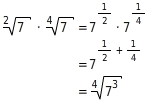
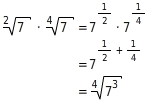
Du schreibst die Wurzeln als Potenzen und wendest das Potenzgesetz für Potenzen mit gleichen Exponenten an.


Du schreibst die Wurzeln als Potenzen und wendest das Potenzgesetz für Potenzen von Potenzen an.
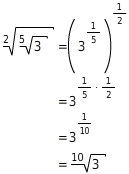
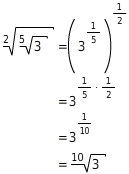
Rationalmachen des Nenners
Wurzeln im Nenner lassen sich durch geschicktes Erweitern vermeiden. Hierzu schreibst du die Wurzel als Potenz und erweiterst anschließend den Bruch so, dass der Exponent im Nenner ganzzahlig wird.
Als Erweiterungsfaktor wählst du die Potenz von 3, die multipliziert mit dem Nenner
die rationale Zahl
ergibt: