Multiplikation und Division von rationalen Zahlen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du rationale Zahlen multiplizierst und dividierst.
Produkt als Summe darstellen
Die Multiplikation mit einer natürlichen Zahl ist in der Mathematik die Vereinfachung einer Additionsaufgabe und kann deshalb auch als fortgesetzte Addition dargestellt werden. Dies ist auch bei rationalen Zahlen möglich.
Multiplikation an der Zahlengeraden
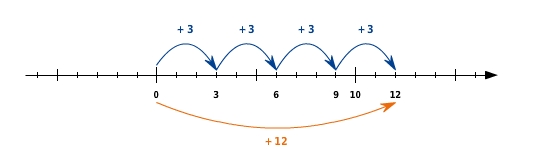
Wenn du zwei positive ganze Zahlen miteinander multiplizierst, dann kannst du das auch über eine fortgesetzte Addition an der Zahlengeraden darstellen.
Du stellst 2 mal 4 dar, indem du zweimal nacheinnander einen Pfeil der Länge 4 nach rechts von der Null ab anträgst. Das Ergebnis ist somit 8.
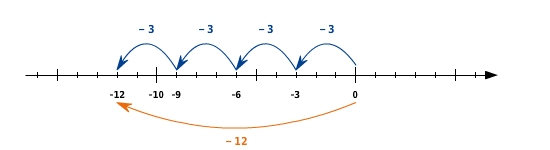
Wenn du eine positive ganze Zahl mit einer negativen ganzen Zahl multiplizierst, dann kannst du dies auch an der Zahlengeraden darstellen.
Du stellst 2 mal (-4) dar, indem du zweimal nacheinander einen Pfeil der Länge 4 nach links von der Null ab anträgst. Das Ergebnis ist somit (-8).
Division von rationalen Zahlen
Die Division von rationalen Zahlen ist die zur Multiplikation entgegengesetzte Rechenart.
Rechenregeln zur Multiplikation und Division von rationalen Zahlen
Bei der Multiplikation oder Division zweier rationaler Zahlen musst du die Vorzeichen der Zahlen beachten.
Haben beide Zahlen ein positives Vorzeichen, dann ist auch das Ergebnis positiv.„plus mal plus ist plus“
Hat die erste Zahl ein positives Vorzeichen und die zweite ein negatives Vorzeichen, dann ist das Ergebnis negativ. „plus mal minus ist minus “
Hat die erste Zahl ein negatives Vorzeichen und die zweite ein positives Vorzeichen, dann ist das Ergebnis negativ. „minus mal plus ist minus “
Haben beide Zahlen ein negatives Vorzeichen, dann ist das Ergebnis positiv. „minus mal minus ist plus“
Multiplikation und Division mit der Null
Bei der Multiplikation mit null ist das Ergebnis immer null.Die Division durch null ist nicht definiert. Das bedeutet, dass du nicht durch 0 dividieren kannst. Wird aber die 0 durch eine beliebige, von 0 verschiedene rationale Zahl dividiert, ist das Ergebnis immer 0.
Multiplikation mit der Null:
Wenn du 3 Eierkartons mit jeweils 0 Eiern füllst, dann hast du insgesamt 0 Eier.
Wenn in einem Produkt einer der Faktoren null ist, dann ist das Produkt immer null.
Division mit der Null:
Diese Aufgabe hat kein Ergebnis, weil die Division durch null nicht definiert ist.
Du sollst 0 Bonbons an 4 Schüler verteilen. Die Antwort ist eindeutig: Jeder Schüler bekommt genau 0 Bonbons.
Multiplikation und Division mit 1 und -1
Die Zahl 1 ist das so genannte neutrale Element der Multiplikation. Das heißt: Wenn du eine beliebige Zahl mit 1 multiplizierst, dann verändert sich die Zahl nicht.
Multiplizierst du eine Zahl mit -1, so verändert sich nur ihr Vorzeichen, der Betrag der Zahl bleibt gleich.
Wenn du eine beliebige Zahl durch 1 dividierst, dann verändert sich die Zahl nicht.
Dividierst du eine Zahl durch -1, so verändert sich nur ihr Vorzeichen, der Betrag der Zahl bleibt gleich.
Rationale Zahlen geschickt multiplizieren
In der Multiplikation gelten das Kommutativgesetz und das Assoziativgesetz.
Das Kommutativgesetz (Vertauschungsgesetz) erlaubt dir, die Faktoren eines Produktes zu vertauschen:
Das Assoziativgesetz (Verbindungsgesetz) erlaubt dir, in Produkten mit mehreren Faktoren auf Klammern zu verzichten:
Deshalb werden Rechenausdrücke, in denen nur das Multiplikationszeichen vorkommt, oft ganz ohne Klammern geschrieben.
Beide Gesetze zusammen bewirken, dass man alle Faktoren einer Multiplikationsaufgabe beliebig vertauschen darf.
Manchmal ist es vorteilhaft die Faktoren zu vertauschen, zum Beispiel wenn zwei Faktoren miteinander multipliziert eine Zehnerpotenz (10, 100, 1000, ...) ergeben.
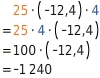Rechne zuerst
.Anschließend multiplizierst du 100 mit (-12,4). Dafür musst du nur noch das Komma verschieben.
Hättest du jedoch von links nach rechts gerechnet, müsstest du zunächst 25 mit (-12,4) multiplizieren. Das ist schon recht schwierig im Kopf auszurechnen.
