Lösen linearer Gleichungssysteme mit drei Variablen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du Gleichungssysteme mit drei Variablen systematisch in Dreiecksgestalt bringst, um sie zu lösen.
Lineare Gleichungssysteme in Dreiecksgestalt lösen
Ein lineares Gleichungssystem ist nur dann eindeutig lösbar, wenn es aus mindestens so vielen Gleichungen besteht wie Variablen darin enthalten sind. Aber auch in diesem Fall ist die eindeutige Lösbarkeit nicht immer gegeben. Wenn ein Dreieckssystem allerdings in Dreiecksgestalt gegeben ist, dann lässt es sich schrittweise durch Einsetzen lösen. 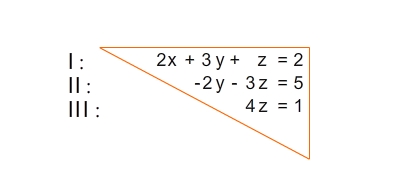
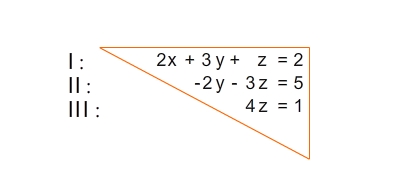
Die Form des Gleichungssystems entspricht einem Dreieck, da von der ersten zur letzten Gleichung jeweils eine Variable weniger in der Gleichung steht.
Löse das Gleichungssystem: 

Gleichungssystem lösen
In Gleichung III gibt es nur die Variable . Du löst nach auf: Den Wert setzt du für in Gleichung II so ein, dass diese Gleichung nur noch die Variable enthält:
Den Wert setzt du für in Gleichung II so ein, dass diese Gleichung nur noch die Variable enthält: Die Lösungen für und setzt du in Gleichung I so ein, dass diese Gleichung nur noch die Variable enthält:
Die Lösungen für und setzt du in Gleichung I so ein, dass diese Gleichung nur noch die Variable enthält: Du erhältst die Lösung =1, =2 und =3 für das lineare Gleichungssystem.
Du erhältst die Lösung =1, =2 und =3 für das lineare Gleichungssystem.


L = { 1 ; 2 ; 3 }
Allgemeines lineares Gleichungssystem mit drei Variablen lösen
Wenn ein lösbares Gleichungssystem nicht in Dreiecksgestalt gegeben ist, kannst du es durch äquivalenzumformungen und Addition oder Subtraktion von Gleichungen in Dreiecksgestalt bringen. Ziel ist es, Variablen so zu eliminieren (zu entfernen), dass du eine Gleichung mit nur einer Variablen, eine weitere Gleichung mit zwei Variablen und schließlich eine dritte mit allen drei Variablen erhältst. Dieses Vorgehen wurde vom Mathematiker Carl Friedrich Gauß entwickelt und wird deshalb Gaußsches Eliminationsverfahren oder Gauß-Algorithmus genannt.
Löse das Gleichungssystem: 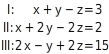
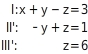
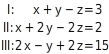
Dreiecksform erzeugen
In den Gleichungen I und II ist der Koeffizient von jeweils 1. Eine Gleichung ohne ergibt sich, indem du Gleichung I mit -1 multiplizierst und das Ergebnis zu Gleichung II addierst.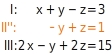 Die ersten beiden Gleichungen passen schon in die Dreiecksgestalt. Du erstellst aus Gleichung I und III eine weitere Gleichung ohne die Variable , indem du Gleichung I mit -2 multiplizierst und das Ergebnis zu Gleichung III addierst. Gleichung III wird durch die neue Gleichung III' (= III + (-2)I) ersetzt:
Die ersten beiden Gleichungen passen schon in die Dreiecksgestalt. Du erstellst aus Gleichung I und III eine weitere Gleichung ohne die Variable , indem du Gleichung I mit -2 multiplizierst und das Ergebnis zu Gleichung III addierst. Gleichung III wird durch die neue Gleichung III' (= III + (-2)I) ersetzt: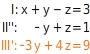 Die Gleichungen II'' und III' enthalten nur noch zwei Variablen. Du multiplizierst Gleichung II'' mit (-3) und addierst die Gleichung zu III'. Du erhältst Gleichung III'' (=III'+(-3)II''), die nur noch die Variable enthält.
Die Gleichungen II'' und III' enthalten nur noch zwei Variablen. Du multiplizierst Gleichung II'' mit (-3) und addierst die Gleichung zu III'. Du erhältst Gleichung III'' (=III'+(-3)II''), die nur noch die Variable enthält.
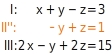
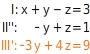
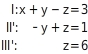
Gleichungssystem lösen
Das Gleichungssystem ist in Dreiecksgestalt: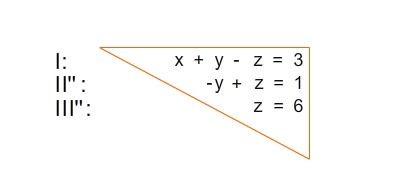 Du löst das Gleichungssystem bei Gleichung III'' beginnend schrittweise durch Einsetzen und Umstellen und berechnest die Lösung.
Du löst das Gleichungssystem bei Gleichung III'' beginnend schrittweise durch Einsetzen und Umstellen und berechnest die Lösung.
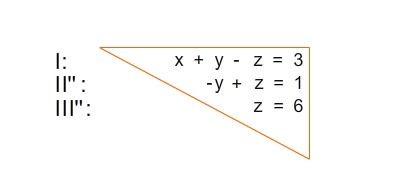
L = { 4 ; 5 ; 6 }
Löse das Gleichungssystem: 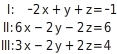
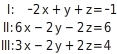
Gleichungssystem lösen
Die Koeffizienten von in Gleichung I und II sind verschieden. Du multiplizierst Gleichung I mit 3 und addierst das Ergebnis zu Gleichung II. Es entfällt die Variable :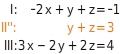 Du multiplizierst Gleichung III mit 2 und Gleichung I mit 3 und addierst die Ergebnisse. So bekommst du eine weitere Gleichung (III') ohne die Variable :
Du multiplizierst Gleichung III mit 2 und Gleichung I mit 3 und addierst die Ergebnisse. So bekommst du eine weitere Gleichung (III') ohne die Variable :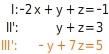 Da die Koeffizienten von in den Gleichungen II' und III' bereits Gegenzahlen voneinander sind, erhältst du durch Addition von Gleichung II' und III' eine Gleichung, in der nur noch die Variable vorkommt. Das Gleichungssystem ist nun in Dreiecksgestalt:
Da die Koeffizienten von in den Gleichungen II' und III' bereits Gegenzahlen voneinander sind, erhältst du durch Addition von Gleichung II' und III' eine Gleichung, in der nur noch die Variable vorkommt. Das Gleichungssystem ist nun in Dreiecksgestalt: Du löst das Gleichungssystem bei Gleichung III'' beginnend schrittweise durch Einsetzen und Umstellen und berechnest die Lösung.
Du löst das Gleichungssystem bei Gleichung III'' beginnend schrittweise durch Einsetzen und Umstellen und berechnest die Lösung.
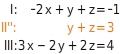
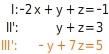

L = { 2 ; 2 ; 1 }

