Lineare Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren- Schnittpunkte mit den Koordinatenachsen
- Die Funktionsgleichung einer linearen Funktion
- Einfluss der Parameter m und b und Spezialfälle
- Graphen zeichnen, wenn zwei Punkte gegeben sind
- Graphen zeichnen, wenn ein Punkt und die Steigung gegeben sind
- Graphen zeichnen, wenn die Geradengleichung gegeben ist
- Funktionsgleichungen aufstellen durch Ablesen am Graphen
- Funktionsgleichungen aufstellen zur Berechnung besonderer Punkte
- Funktionsgleichungen mit der Punkt-Steigungs-Formel bestimmen
- Funktionsgleichungen mit Hilfe von zwei Punkten bestimmen
- Von der graphischen Darstellung zur Wertetabelle
- Berechnen der Nullstelle
- Berechnen des y-Achsenabschnitts
- Bedeutung der Achsenabschnitte in Sachsituationen
- Schnittpunkt zweier Funktionsgraphen
- Parallele Geraden
- Lagebeziehungen zweier Geraden ermitteln
- Gerade mit vorgegebener Steigung zeichnen
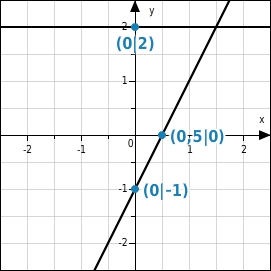
Schnittpunkte mit den Koordinatenachsen
Der Graph einer linearen Funktion f mit der Funktionsgleichung
(und uneingeschränktem Definitionsbereich) schneidet die y-Achse im Punkt
.
Einen Schnittpunkt x 0 | 0 mit der x-Achse gibt es dann, wenn m≠0. Für
ist der Graph eine Gerade parallel zur x-Achse.

Eine Gerade, die parallel zu y-Achse verläuft, ist kein Funktionsgraph. Zu einem x-Wert gehören in diesem Fall mehrere y-Werte.


Ist die Steigung der Geraden -1 und b ungleich 0, dann schneidet die Gerade die Koordinatenachsen so, dass ein gleichschenkliges Dreieck entsteht, der y-Achsenabschnitt und die Nullstelle haben den gleichen Wert.


In diesem Fall ist dann
und
Die Schnittpunkte mit den Koordinatenachsen kannst du mit Hilfe der Parameter in der Geradengleichung in Normalform
schnell bestimmen.
Den y-Achsenabschnitt kannst du direkt ablesen, die Gerade schneidet die y-Achse im Punkt (0|b).
Die Nullstelle berechnest du, indem du für y den Wert 0 einsetzt und die Gleichung nach x auflöst.
Die Gerade schneidet die x-Achse im Punkt (
|
)
Die Gerade g mit der Gleichung
schneidet die y-Achse im Punkt (
|
) und die x-Achse im Punkt (
|
).
Ist der y-Achsenabschnitt
, so nennt man die Gerade Ursprungsgerade.


Die Funktionsgleichung einer linearen Funktion
Auch anhand der Funktionsgleichung kannst du lineare Funktionen von anderen unterscheiden.
Eine Kurve verläuft dann geradlinig, wenn sich bei gleichmäßiger Erhöhung (oder Verminderung) der x-Werte (Argumente) auch die y-Werte (Funktionswerte) gleichmäßig erhöhen (oder vermindern).
Das ist genau dann der Fall, wenn im Funktionsterm die Variable x nur mit einem Faktor (der Steigung) multipliziert wird. Dieser gibt an, wie stark die Funktionswerte zu- bzw. abnehmen, wenn sich x ändert.
Der Graph der Funktion f wird beschrieben durch die Geradengleichung
.
Immer wenn sich der Wert für x um 1 erhöht, erhöht sich der Funktionswert um 2, denn die Variable x wird mit 2 multipliziert.
Außerdem kann die Gleichung einen weiteren Summanden enthalten, das so genannte Absolutglied.
Dieses gibt an, an welcher Stelle die Gerade die y-Achse schneidet und wird daher auch y-Achsenabschnitt genannt.
Die Graphen der Funktionen h, g und i werden beschrieben durch die Geradengleichungen:

Der Graph der Funktion h verläuft parallel zum Graphen der Funktion f und ist um 3 Einheiten nach oben verschoben.Der Graph der Funktion g verläuft parallel zum Graphen der Funktion f und ist um 2 Einheiten nach unten verschoben.Der Graph der Funktion i verläuft parallel zur x-Achse.
 Die Gleichung einer linearen Funktion hat immer die Gestalt
. Sie wird auch Normalform der Geradengleichung genannt.Dabei ist m die Steigung und b der y-Achsenabschnitt der Funktion.
Die Gleichung einer linearen Funktion hat immer die Gestalt
. Sie wird auch Normalform der Geradengleichung genannt.Dabei ist m die Steigung und b der y-Achsenabschnitt der Funktion.
Im Fall
ist die Steigung m = 2 und der y-Achsenabschnitt b = 0.Im Fall
ist die Steigung ebenfalls m = 2. Der y-Achsenabschnitt ist b = -2.Für den Fall
ist die Steigung m = 0 und der y-Achsenabschnitt b = 3.
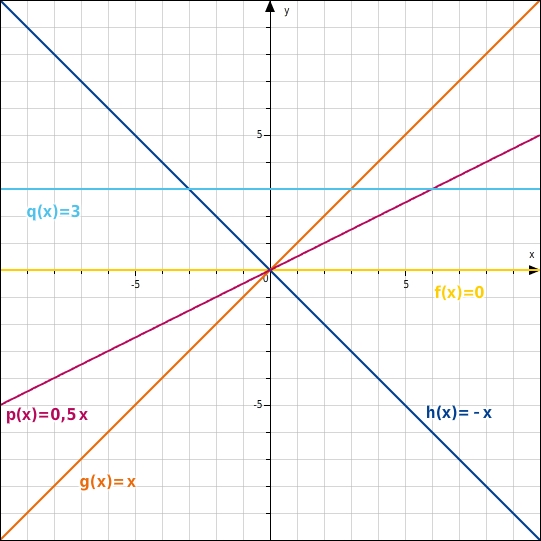
Einfluss der Parameter m und b und Spezialfälle
Die Parameter m und b in der Funktionsgleichung
bestimmen den jeweiligen Verlauf des Graphen. Dabei ist m das Maß der Steigung und b bewirkt eine Verschiebung entlang der y-Achse.Je nach Belegung der Parameter m und b ergeben sich verschiedene Spezialfälle.
b = 0 ⇒
Der Graph der zugehörigen Funktion geht durch den Punkt 0 | 0 , egal, welchen Wert du für m einsetzt, denn
.Geraden durch den Koordinatenursprung heißen Ursprungsgeraden.
m = 0 ⇒
Der Graph der zugehörigen Funktion ist parallel zur x-Achse, denn für jedes x ist
.
m = 0 und b = 0 ⇒
Diese Gleichung beschreibt die x-Achse.
m = 1, b = 0 ⇒
Diese Gleichung beschreibt die Winkelhalbierende der Quadranten I und III, auch 1. Winkelhalbierende genannt.
m = -1, b = 0 ⇒
Diese Gleichung beschreibt die Winkelhalbierende der Quadranten II und IV, auch 2. Winkelhalbierende genannt.
Die Abbildung zeigt alle diese Spezialfälle in einem Koordinatensystem.
Graphen zeichnen, wenn zwei Punkte gegeben sind
Der Graph einer linearen Funktion ist eine Gerade.Zum Zeichnen einer Geraden benötigst du mindestens 2 Punkte.Hast du von einer linearen Funktion zwei Wertepaare gegeben, kannst du den Funktionsgraphen durch die zugehörigen Punkte zeichnen.
Zeichne den Graphen der linearen Funktion
, zu dem die Punkte
(3|4) und
(-1|-2) gehören.

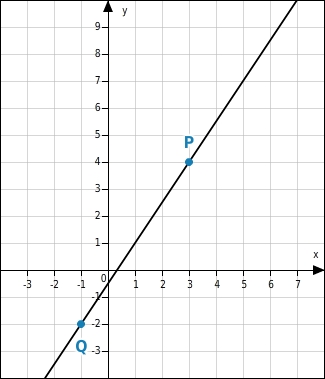
Punkte im Koordinatensystem eintragen
Beachte beim Eintragen der Punkte die Reihenfolge der Koordinaten. Der erste Wert ist der
-Wert, der zweite der
-Wert.

Gerade zeichnen
Du zeichnest durch die Punkte eine Gerade. Diese Gerade ist der Graph der Funktion
.

Graphen zeichnen, wenn ein Punkt und die Steigung gegeben sind
Auch durch einen Punkt und die Steigung ist eine Gerade eindeutig bestimmt.
Du trägst den gegebenen Punkt ins Koordinatensystem ein und nutzt das Steigungsdreieck, um einen weiteren Punkt des Graphen zu erhalten.
Zeichne die Gerade durch den Punkt
(-2|5) mit der Steigung
.


Punkt ins Koordinatensystem eintragen

Gerade mit Hilfe des Steigungsdreiecks zeichnen
Die Steigung ist negativ (
0). Also verläuft die Gerade von oben links nach unten rechts.Mit jeder Einheit nach rechts, fällt die Gerade um 2 Einheiten.Vom Punkt
aus trägst du die Steigung -2 ab (1 nach rechts und 2 nach unten) und markierst den Punkt
(-1|3).Durch die Punkte
und
zeichnest du die Gerade.Das eingetragene Dreieck nennt man Steigungsdreieck.

Gegeben ist der Punkt
(-2|-3), der zu der Geraden
mit der Steigung
=
gehört.
Zeichne die Gerade.
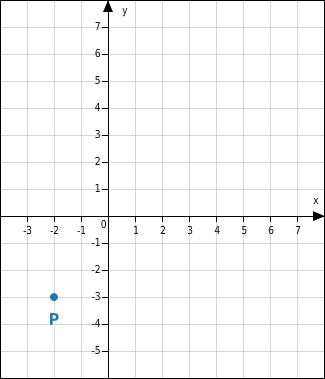

Punkt ins Koordinatensystem eintragen

Gerade mit Hilfe des Steigungsdreiecks zeichnen
Die Steigung ist positiv (
> 0). Also verläuft die Gerade von unten links nach oben rechts.Vom Punkt
aus trägst du die Steigung
=
ab (4 nach rechts und 3 nach oben) und markierst den Punkt
(2|0).Durch die Punkte
und
zeichnest du die Gerade.

Der Punkt
(2|-4) liegt auf einer Geraden mit der Steigung
= 2,5.
Zeichne die Gerade mit Hilfe eines Steigungsdreiecks.

Punkt ins Koordinatensystem eintragen

Steigung als Bruch angeben
Du wandelst die Dezimalzahl in einen Bruch um:
2,5 =
=
=
Gerade mit Hilfe des Steigungsdreiecks zeichnen
Die Steigung ist positiv (
> 0). Also verläuft die Gerade von unten links nach oben rechts.Vom Punkt
aus trägst du die Steigung
=
ab (2 nach rechts und 5 nach oben) und markierst den Punkt
(4|1).Durch die Punkte
und
zeichnest du die Gerade.

Graphen zeichnen, wenn die Geradengleichung gegeben ist
Hast du die Funktionsgleichung der linearen Funktion gegeben, nutzt du zum Zeichnen des Graphen den
-Achsenabschnitt und die Steigung. Beides kannst du der Gleichung in Normalform direkt entnehmen.
Gegeben ist die Funktion
mit der Gleichung
.
Zeichne den Graphen der Funktion
.

-Achsenabschnitt bestimmen
Die Funktionsgleichung entspricht der Normalform der Geradengleichung:
Der
-Achsenabschnitt ist
.Die Gerade schneidet die
-Achse im Punkt (0|2).
= 2
Steigung als Bruch angeben
Du wandelst die Dezimalzahl in einen Bruch um:
=
Gerade mit
-Achsenabschnitt und Steigungsdreieck zeichnen
Die Steigung ist negativ, die Gerade fällt.Du gehst vom Punkt
2 Einheiten nach rechts und 3 Einheiten nach unten und gelangst so zum Punkt
(2|-1).Die Gerade zeichnest du durch die Punkte
und
.

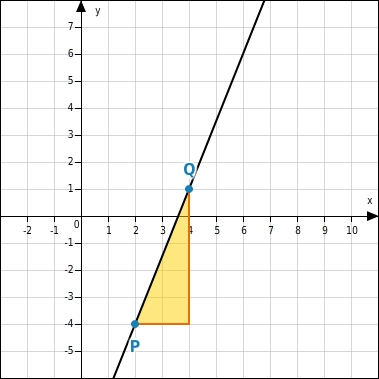
Gegeben ist die Gleichung
.
Zeichne die zugehörige Gerade.

Normalform bestimmen
Du bestimmst die Normalform der Geradengleichung, indem du sie mit äquivalenzumformungen nach
umstellst.
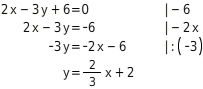
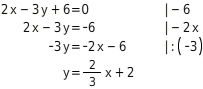
Gerade mit
-Achsenabschnitt und Steigung zeichnen
Die Steigung ist
, der
-Achsenabschnitt ist 2.Du gehst vom Punkt
(0|2) 3 Einheiten nach rechts und 2 Einheiten nach oben und gelangst so zum Punkt
(3|4).Die Gerade zeichnest du durch die Punkte
und
.

Zeichne die Graphen der beiden linearen Funktionen
und
ins Koordinatensystem und bestimme ihren Schnittpunkt.
:
:
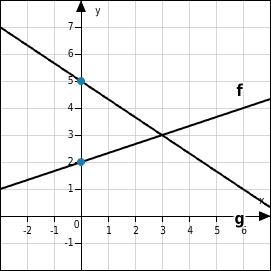

Geraden zeichnen
Du zeichnest die Geraden mit Hilfe der jeweiligen
-Achsenabschnitte
und Steigungen
:
:
;
= 2
:
;
= 5

Schnittpunkt ablesen
(3|3)

Funktionsgleichungen aufstellen durch Ablesen am Graphen
Der Graph einer linearen Funktion ist eine Gerade. Die Gleichung hat die Form
.
Dabei bezeichnet
den Wert für die Steigung und
den
-Achsenabschnitt.
Hast du von einer linearen Funktion den Graphen, also die Gerade gegeben, kannst du beide Werte direkt der graphischen Darstellung entnehmen.
Bestimme zum abgebildeten Graphen die Funktionsgleichung.


Gleichung aufstellen
Die Gerade schneidet die y-Achse an der Stelle -4  Am Steigungsdreieck kannst du ablesen, dass die Gerade die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade die Steigung
hat.
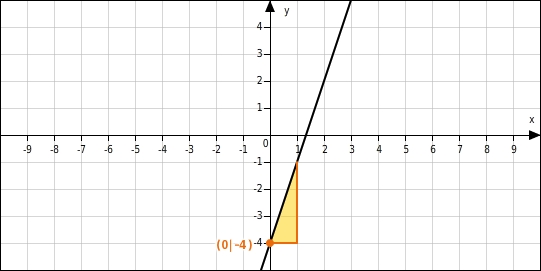

Bestimme zum abgebildeten Graphen die Funktionsgleichung.


Gleichung aufstellen
Die Gerade schneidet die y-Achse an der Stelle 1  Am Steigungsdreieck kannst du ablesen, dass die Gerade hat die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade hat die Steigung
hat.
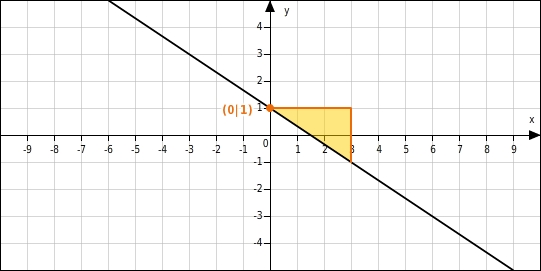

Funktionsgleichungen aufstellen zur Berechnung besonderer Punkte
Viele Zusammenhänge in Natur und Technik lassen sich durch lineare Funktionen beschreiben.
Oft haben die besonderen Punkte der Graphen (Nullstelle, y-Achsenabschnitt, Schnittpunkte mit anderen Graphen) in diesen Beispielen auch eine besondere Bedeutung.
In einer Region ist eine bestimmte Pflanzenart an einem Virus erkrankt. Der Prozentsatz der kranken Pflanzen wird alle 5 Jahre erfasst und registriert.
Eine lineare Funktion beschreibt den Trend recht gut, der Anteil der kranken Pflanzen nimmt ab, die Pflanzen werden immun gegen den Virus.
Bei der ersten Zählung werden
der Pflanzen als krank gezählt.
Welcher Anteil der Pflanzen wird nach 70 Jahren noch krank sein?
Wann wird es voraussichtlich in dieser Region erstmalig keine kranken Pflanzen mehr geben?

 Die Steigung der Geraden ermittelst du mit Hilfe eines Steigungsdreiecks:
Die Gerade schneidet die y-Achse an der Stelle
. Bei der ersten Zählung waren
aller Pflanzen erkrankt.
Die Steigung der Geraden ermittelst du mit Hilfe eines Steigungsdreiecks:
Die Gerade schneidet die y-Achse an der Stelle
. Bei der ersten Zählung waren
aller Pflanzen erkrankt.

Funktionsgleichung aufstellen
 Die Steigung der Geraden ermittelst du mit Hilfe eines Steigungsdreiecks:
Die Gerade schneidet die y-Achse an der Stelle
. Bei der ersten Zählung waren
aller Pflanzen erkrankt.
Die Steigung der Geraden ermittelst du mit Hilfe eines Steigungsdreiecks:
Die Gerade schneidet die y-Achse an der Stelle
. Bei der ersten Zählung waren
aller Pflanzen erkrankt.
Funktionswert berechnen
Du setzt den Wert 70 für x in die Funktionsgleichung ein und berechnest y.
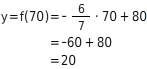
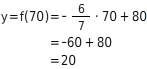
Nullstelle berechnen
Der berechnete Zeitpunkt, zu dem voraussichtlich keine kranken Pflanzen mehr gezählt werden, entspricht der Nullstelle der Funktion.
Du berechnest die Nullstelle (f(x) = 0) indem du 0 für y in die Funktionsgleichung einsetzt und die Gleichung nach x auflöst.
 Da die Zählung alle 5 Jahre stattfindet, wird man voraussichtlich erstmalig bei der Zählung nach 95 Jahren keine kranken Pflanzen mehr finden.
Da die Zählung alle 5 Jahre stattfindet, wird man voraussichtlich erstmalig bei der Zählung nach 95 Jahren keine kranken Pflanzen mehr finden.
 Da die Zählung alle 5 Jahre stattfindet, wird man voraussichtlich erstmalig bei der Zählung nach 95 Jahren keine kranken Pflanzen mehr finden.
Da die Zählung alle 5 Jahre stattfindet, wird man voraussichtlich erstmalig bei der Zählung nach 95 Jahren keine kranken Pflanzen mehr finden.
Funktionsgleichungen mit der Punkt-Steigungs-Formel bestimmen
Hast du von der Funktion die Steigung und einen Punkt des Graphen gegeben, kannst du den y-Achsenabschnitt rechnerisch bestimmen.
Der Graph einer linearen Funktion f verläuft durch den Punkt P(
|
) und hat die Steigung
.
Bestimme die Funktionsgleichung von f.
Der Punkt Q(
|y) liege ebenfalls auf dem Graphen der Funktion.
Bestimme die y-Koordinate.
Funktionsgleichung angeben
Der Punkt P(
|
) liegt auf der Geraden. Also erfüllen seine Koordinaten die zugehörige Funktionsgleichung.
Die Funktionsgleichung hat die Form
Du bestimmst den y-Achsenabschnitt b, indem du die Koordinaten des Punktes P in die Funktionsgleichung einsetzt und die Gleichung nach b auflöst:


y-Koordinate des Punktes Q bestimmen
Du setzt die x-Koordinate des Punktes Q in die Funktionsgleichung ein und berechnest y.
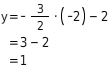
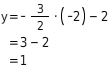
Q(
|
)
Funktionsgleichungen mit Hilfe von zwei Punkten bestimmen
Hast du von der Funktion zwei Punkte P und Q des Graphen gegeben, kannst du die Steigung mit Hilfe der Steigungsformel
rechnerisch bestimmen.
Mit Hilfe der Funktionsgleichung kannst du dann überprüfen, ob ein beliebiger weiterer Punkt auch auf dem Graphen der Funktion liegt.
Bestimme die Funktionsgleichung zur Geraden, die durch die Punkte P(
|
) und Q(
|
) verläuft.
überprüfe, ob die Punkte R(
|
) und S(
|
) auf der Geraden liegen.

Steigung mit Hilfe der Steigungsformel berechnen
Du setzt die Koordinaten der Punkte P und Q in die Steigungsformel ein und berechnest die Steigung.

y-Achsenabschnitt bestimmen und Funktionsgleichung angeben
Du setzt die Koordinaten eines der beiden Punkte in die Funktionsgleichung
ein und löst die Gleichung nach b auf.
Mit P(
|
) gilt:
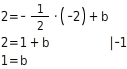
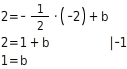
Zugehörigkeit des Punktes R überprüfen
Du setzt die Koordinaten des Punktes R in die Funktionsgleichung ein und überprüfst, ob eine wahre Aussage entsteht.


Der Punkt R(
|
) liegt auf der Geraden.
Zugehörigkeit des Punktes S überprüfen
Du setzt die Koordinaten des Punktes S in die Funktionsgleichung ein und überprüfst, ob eine wahre Aussage entsteht.


Der Punkt S(
|
) liegt nicht auf der Geraden.
Von der graphischen Darstellung zur Wertetabelle
Du kannst mit Hilfe einer graphischen Darstellung eine Wertetabelle erstellen oder eine Wertetabelle ergänzen.
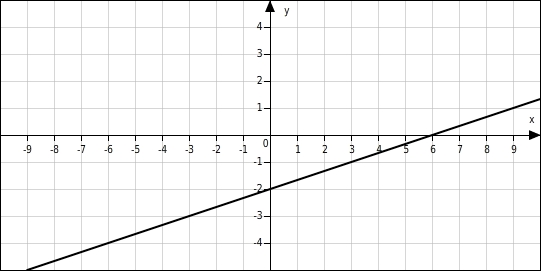
Gegeben ist der Graph einer linearen Funktion. Ergänze in der Wertetabelle die fehlenden x-Koordinaten.





x-Werte ergänzen
Du suchst auf der Geraden die Punkte, deren y-Koordinaten mit denen in der Wertetabelle übereinstimmen und liest an der x-Achse die dazu gehörenden x-Werte ab.



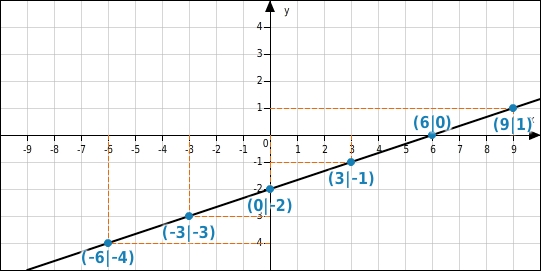
Gegeben ist der Graph einer linearen Funktion. Ergänze in der Wertetabelle die fehlenden y-Koordinaten.




y-Werte ergänzen
Du suchst auf der Geraden die Punkte, deren x-Koordinaten mit denen in der Wertetabelle übereinstimmen und liest an der y-Achse die dazu gehörenden y-Werte ab.


Berechnen der Nullstelle
Du kannst die Nullstelle
auch mit Hilfe der Funktionsgleichung berechnen.
Der Schnittpunkt mit der x-Achse hat die Koordinaten (
|
).
Du setzt also in der Funktionsgleichung
für y den Wert 0 ein und löst die Gleichung nach x auf.
Berechne die Nullstelle der Funktion f mit
.
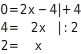
y-Koordinate einsetzen
Gleichung lösen
Du löst die Gleichung mit Hilfe von äquivalenzumformungen.
Die Nullstelle der Funktion f ist 2.
Der Graph der Funktion schneidet die x-Achse im Punkt (
|
).
 Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
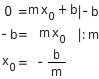
 Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
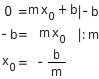
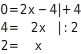
Berechnen des y-Achsenabschnitts
Wenn vom Graphen einer linearen Funktion ein Punkt und die Steigung gegeben sind, kannst du den y-Achsenabschnitt berechnen.
Bestimme den y-Achsenabschnitt der Funktion f mit der Steigung
, für die der Punkt P(
|
) zum Graphen gehört.

Koordinaten des Punktes in die Funktionsgleichung einsetzen
Du setzt den Wert 1 für y, den Wert 4 für x und den Wert
für m in die Gleichung
ein.

y-Achsenabschnitt bestimmen
Du löst die Gleichung mit Hilfe von äquivalenzumformungen:
 Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
 Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
Bedeutung der Achsenabschnitte in Sachsituationen
In Sachsituationen haben die Achsenabschnitte eine besondere Bedeutung.
Der y-Achsenabschnitt steht meist für einen Anfangswert, z. B. Startguthaben, Grundgebühr, Vorsprung usw.
Susanne arbeitet neben ihrem Studium als Aushilfe im Stadttheater an der Garderobe. Sie bekommt vom Veranstalter
Wechselgeld und nimmt dann pro abgegebener Jacke
ein.
Die Zuordnung
Anzahl der Jacken  Betrag in der Kasse in €
kannst du mit einer linearen Funktion beschreiben (
=
):
Der Anfangsbetrag in der Kasse (
) entspricht dem y-Achsenabschnitt.
Betrag in der Kasse in €
kannst du mit einer linearen Funktion beschreiben (
=
):
Der Anfangsbetrag in der Kasse (
) entspricht dem y-Achsenabschnitt.
Die Nullstelle kann z. B. ein Zeitpunkt sein, zu dem ein Becken leer gepumpt ist oder eine Anzahl an Tagen, nach denen ein Vorrat aufgebraucht ist.
Die Nullstelle bildet in Sachsituationen eine Grenze des Definitionsbereichs, wenn die Funktionswerte davor oder danach kleiner als 0 sind und es solche Werte nicht geben kann, z.B. einen negativen Inhalt eines Beckens oder einen negativen Vorrat.
Frau Meier verreist für einige Tage. Damit ihre Pflanzen auf dem Fensterbrett nicht vertrocknen, stellt sie einen Eimer mit
Wasser daneben und verlegt zu jedem Blumentopf einen Wollfaden, der mit einem Ende im Wasser hängt und mit dem anderen Ende in der Erde steckt.
 Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
 Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
Die Zuordnung
Anzahl der Stunden  Wassermenge im Eimer in Litern
kannst du mit einer linearen Funktion beschreiben (
=
):
Die Anzahl der Stunden, nach denen der Eimer leer ist, entspricht der Nullstelle der Funktion.
Der Eimer ist nach 45 Stunden leer.
Wassermenge im Eimer in Litern
kannst du mit einer linearen Funktion beschreiben (
=
):
Die Anzahl der Stunden, nach denen der Eimer leer ist, entspricht der Nullstelle der Funktion.
Der Eimer ist nach 45 Stunden leer.
Schnittpunkt zweier Funktionsgraphen
Haben zwei lineare Funktionen verschiedene Steigungen, so schneiden sich die Graphen in einem Punkt.
Dieser Schnittpunkt ist von Bedeutung, wenn du dich z.B. zwischen zwei Möglichkeiten entscheiden möchtest.
Marie möchte sich ein Handy kaufen und vergleicht vorher einige Handytarife.

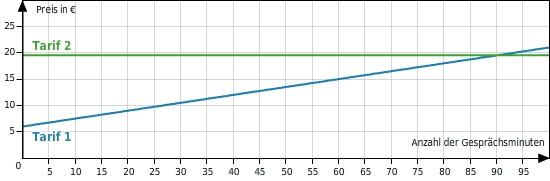 Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?
Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?

 Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?
Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?
Die Geraden mit den Steigungen 0,15 bzw 0 schneiden sich im Punkt (
|
).
Für alle Werte von x, die kleiner sind als 90, verläuft der Graph der Funktion, die den Tarif 1 beschreibt, unterhalb des Graphen der Funktion zu Tarif 2.
Mia sollte also bei einer voraussichtlichen Gesprächsdauer von 50 Minuten pro Monat den Tarif 1 wählen.
Erst ab einer Gesprächsdauer von 90 Minuten wird die Flatrate günstiger.


Parallele Geraden
Parallele Geraden haben keinen Schnittpunkt. Der Abstand zweier paralleler Geraden ist überall gleich, denn parallele Geraden haben dieselbe Steigung.


Zeichne die Parallele h zur Geraden g durch den Punkt P.



Parallele zeichnen
Du ermittelst die Steigung der Geraden g (
) und trägst diese Steigung am Punkt P an.Du kannst dazu ein Steigungsdreieck einzeichnen.



Vervollständige die Gleichung der Geraden h so, dass die Geraden g und h parallel sind.h: y = __

 Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.

Steigung der Geraden g bestimmen
 Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Geradengleichung für h vervollständigen
Parallele Geraden haben dieselbe Steigung


h:
Lagebeziehungen zweier Geraden ermitteln
Um die Lagebeziehung zweier Geraden g und h zu bestimmen, musst du die Geraden nicht in ein Koordinatensystem einzeichnen. Es reicht die Betrachtung der Geradengleichungen in Normalform.Für die Geraden g und h mit den Gleichungen (
) bzw. (
) gilt:
•
und
≠
 Geraden g und h sind parallel.
•
Geraden g und h sind parallel.
•
 Geraden g und h stehen senkrecht aufeinander.
•
und
Geraden g und h stehen senkrecht aufeinander.
•
und
 Geraden sind Spiegelbilder voneinander mit der y-Achse als Spiegelachse.
•
und
Geraden sind Spiegelbilder voneinander mit der y-Achse als Spiegelachse.
•
und
 Geraden sind Spiegelbilder voneinander mit der x-Achse als Spiegelachse.
Geraden sind Spiegelbilder voneinander mit der x-Achse als Spiegelachse.
Gegeben sind die Geradengleichungen der Geraden f, g, h und k. Wie liegen diese Geraden zueinander?
f:
g:
h:
k:

Lagebeziehungen ermitteln

Die Geraden f und g liegen spiegelsymmetrisch bezüglich der x-Achse.
Die Geraden fund h liegen spiegelsymmetrisch bezüglich der y-Achse.
Die Geraden g und h sind parallel zueinander.
Die Geraden f und k stehen senkrecht aufeinander.
Gerade mit vorgegebener Steigung zeichnen
Mit Hilfe des Steigungsdreiecks kannst du eine Gerade in ein Koordinatensystem zeichnen.
Gegeben ist die Gerade g und der Schnittpunkt 0 | 3 mit der y-Achse. Verschiebe den orangen Punkt so, dass die Gerade die Steigung
hat.



orangen Punkt verschieben
Steigung
bedeutet, dass sich die y-Werte um 4 verkleinern, wenn sich die x-Werte um 3 vergrößern.Du nutzt das Steigungsdreieck mit den Seitenlängen 3 und 4 und gehst vom Punkt 0 | 3 aus 3 Einheiten nach rechts und 4 Einheiten nach unten und gelangst zum Punkt (3|-1). Hier lässt du den orangen Punkt los.
Es wäre auch ein anderes Steigungsdreieck möglich:
 Verwendest du das negative Vorzeichen für den Nenner, so gehst du 3 Einheiten nach links und 4 Einheiten nach oben.
Verwendest du das negative Vorzeichen für den Nenner, so gehst du 3 Einheiten nach links und 4 Einheiten nach oben.
 Verwendest du das negative Vorzeichen für den Nenner, so gehst du 3 Einheiten nach links und 4 Einheiten nach oben.
Verwendest du das negative Vorzeichen für den Nenner, so gehst du 3 Einheiten nach links und 4 Einheiten nach oben.


