Lagebeziehungen von Geraden
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du anhand der Geradengleichungen entscheiden kannst, welche Lagebeziehung zwei Geraden zueinander haben.
Parallele Geraden
Parallele Geraden haben keinen Schnittpunkt. Der Abstand zweier paralleler Geraden ist überall gleich, denn parallele Geraden haben dieselbe Steigung.


Zeichne die Parallele h zur Geraden g durch den Punkt P.

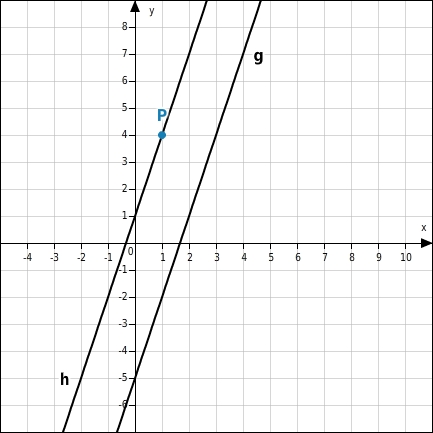

Parallele zeichnen
Du ermittelst die Steigung der Geraden g (
) und trägst diese Steigung am Punkt P an.Du kannst dazu ein Steigungsdreieck einzeichnen.



Vervollständige die Gleichung der Geraden h so, dass die Geraden g und h parallel sind.h: y = __

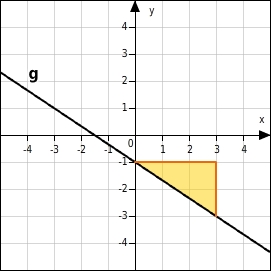 Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.

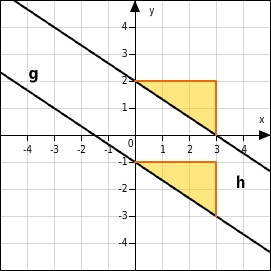
Steigung der Geraden g bestimmen
 Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Geradengleichung für h vervollständigen
Parallele Geraden haben dieselbe Steigung

h:
Senkrechte Geraden
Zueinander senkrechte Geraden schneiden sich einem Winkel von
. Sind die Geraden g und h senkrecht zueinander, dann gilt für die Steigungen
und
:


Zeichne die Senkrechte h zur Geraden g durch den Punkt P.

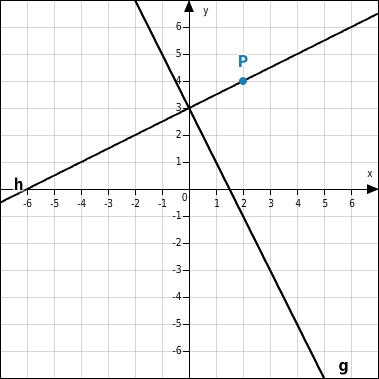

Senkrechte zeichnen
Du ermittelst die Steigung der Geraden g (
)) und bestimmst damit die Steigung der Senkrechten h:
Diese Steigung trägst du am Punkt P an.Du kannst dazu ein Steigungsdreieck einzeichnen.
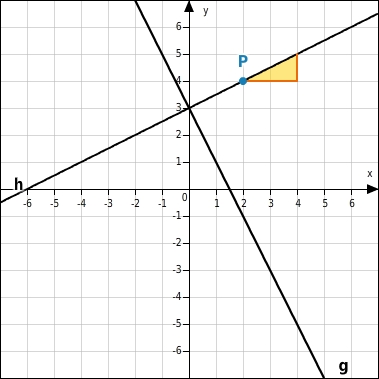


Vervollständige die Gleichung der Geraden h so, dass die Geraden g und h senkrecht aufeinander stehen.
h: y = __
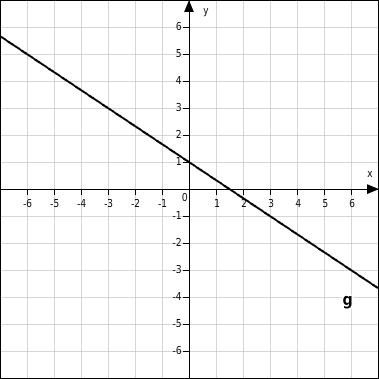
 Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.

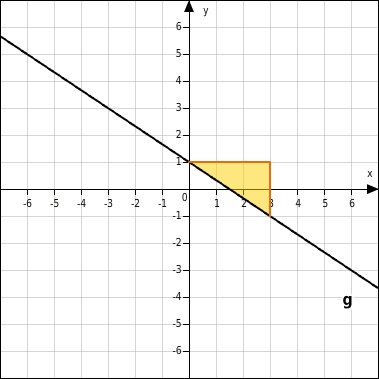
Steigung der Geraden g bestimmen
 Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Am Steigungsdreieck kannst du ablesen, dass die Gerade g die Steigung
hat.
Geradengleichung für h vervollständigen

h:
Spiegeln von Geraden an den Koordinatenachsen
Bei einer Spiegelung an der y-Achse wird jeder Punkt (x|y) auf den Punkt (-x|y) abgebildet.Spiegelst du eine Gerade g mit
an der y-Achse, so erhältst du die Bildgerade h mit der Gleichung
.
Für die Steigungen gilt:
Für die y-Achsenabschnitte gilt:
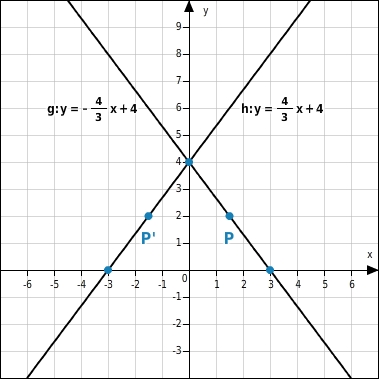

Die Gerade g wird an der y-Achse gespiegelt. Gib die Gleichung der Bildgeraden h an.
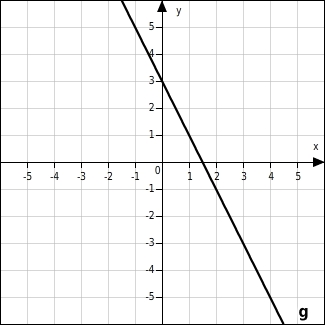

Gleichung für Gerade h ermitteln
Du ermittelst die Steigung der Geraden g (
) und bestimmst damit die Steigung der Bildgeraden g‘.
Diese Steigung trägst du am Schnittpunkt mit der y-Achse 0 | 3 an.Du kannst dazu ein Steigungsdreieck einzeichnen.


g‘:
Bei einer Spiegelung an der x-Achse wird jeder Punkt (x|y) auf den Punkt (x|-y) abgebildet.Spiegelst du eine Gerade g mit
an der x-Achse, so erhältst du die Bildgerade h mit der Gleichung
.
Für die Steigungen gilt:
Für die y-Achsenabschnitte gilt:
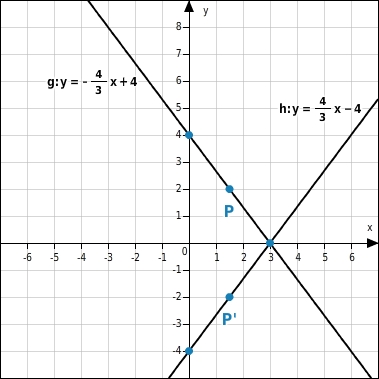

Die Gerade g wird an der x-Achse gespiegelt. Gib die Gleichung der Bildgeraden h an.
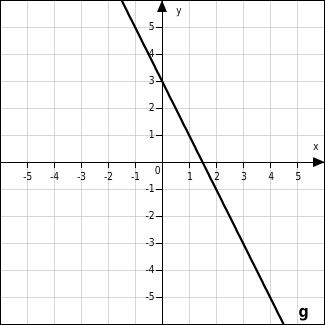

Gleichung für Gerade h ermitteln
Du ermittelst die Steigung der Geraden g (
) und bestimmst damit die Steigung der Bildgeraden g‘.
Ebenso bestimmst du den y-Achsenabschnitt der Geraden g?.
Die Steigung trägst du anschließend am Schnittpunkt mit der y-Achse (0|-3) an.Du kannst dazu ein Steigungsdreieck einzeichnen.


g‘:
Lagebeziehungen zweier Geraden ermitteln
Um die Lagebeziehung zweier Geraden g und h zu bestimmen, musst du die Geraden nicht in ein Koordinatensystem einzeichnen. Es reicht die Betrachtung der Geradengleichungen in Normalform.Für die Geraden g und h mit den Gleichungen (
) bzw. (
) gilt:
•
und
≠
 Geraden g und h sind parallel.
•
Geraden g und h sind parallel.
•
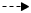 Geraden g und h stehen senkrecht aufeinander.
•
und
Geraden g und h stehen senkrecht aufeinander.
•
und
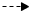 Geraden sind Spiegelbilder voneinander mit der y-Achse als Spiegelachse.
•
und
Geraden sind Spiegelbilder voneinander mit der y-Achse als Spiegelachse.
•
und
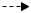 Geraden sind Spiegelbilder voneinander mit der x-Achse als Spiegelachse.
Geraden sind Spiegelbilder voneinander mit der x-Achse als Spiegelachse.
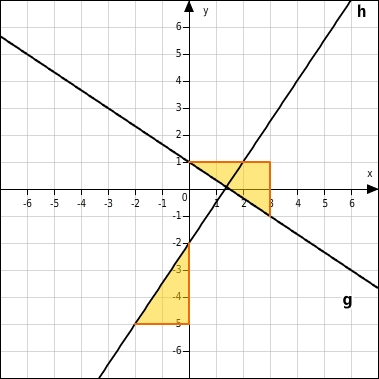
Gegeben sind die Geradengleichungen der Geraden f, g, h und k. Wie liegen diese Geraden zueinander?
f:
g:
h:
k:

Lagebeziehungen ermitteln

Die Geraden f und g liegen spiegelsymmetrisch bezüglich der x-Achse.
Die Geraden fund h liegen spiegelsymmetrisch bezüglich der y-Achse.
Die Geraden g und h sind parallel zueinander.
Die Geraden f und k stehen senkrecht aufeinander.

