Irrationale Zahlen kennenlernen
Online Mathe üben mit bettermarks
- Über 2.000 Übungen mit über 100.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
In diesen Erklärungen erfährst du, welche Beziehungen zwischen den Mengen der rationalen, der irrationalen und der reellen Zahlen bestehen.
Die rationalen Zahlen
Die Menge der Rationalen Zahlen (ℚ) besteht aus allen Zahlen, die als Quotient zweier ganzer Zahlen dargestellt werden können.
Da sich alle natürlichen Zahlen als
darstellen lassen, sind natürliche und ganze Zahlen auch rationale Zahlen.
Da sich alle natürlichen Zahlen als
darstellen lassen, sind natürliche und ganze Zahlen auch rationale Zahlen.
Die Zahlen
,
,
,
… sind rationale Zahlen.
Du kannst sie als unechten Bruch darstellen. Zum Beispiel:
oder
Eine Dezimalzahl ist eine rationale Zahl, wenn sie …
,
,
und
sind rationale Zahlen.
Alle diese Dezimalzahlen kannst du also auch als Bruch oder als gemischte Zahl angeben.
Die irrationalen Zahlen
Irrationale Zahlen sind Zahlen, die nicht als Quotient ganzer Zahlen dargestellt werden können.
Irrationale Zahlen sind Dezimalzahlen mit unendlich vielen Stellen nach dem Komma, die sich nicht periodisch wiederholen.
Hierzu gehören z.B. die Wurzeln aus natürlichen Zahlen, die keine Quadratzahlen sind.
Auch die Kreiszahl
… ist eine irrationale Zahl - sie ist keine periodische Dezimalzahl.
Durch die irrationalen Zahlen wird der Zahlbereich ℚ der rationalen Zahlen erweitert zum Zahlbereich ℝ der reellen Zahlen.
ist eine irrationale Zahl.
≈
…
Die Anzahl der Stellen nach dem Komma von
ist weder endlich noch wiederholen sie sich periodisch.
Nicht alle Wurzeln sind irrational.
ist keine irrationale Zahl.
ist eine natürliche Zahl, da 25 eine Quadratzahl ist.
ist keine irrationale Zahl.
kann also als Bruch dargestellt werden und ist daher eine rationale Zahl.
Die reellen Zahlen
Die Menge der reellen Zahlen ℝ besteht aus den rationalen Zahlen und den irrationalen Zahlen.
Der Bereich der reellen Zahlen schließt die anderen dir bekannten Zahlbereiche ein:
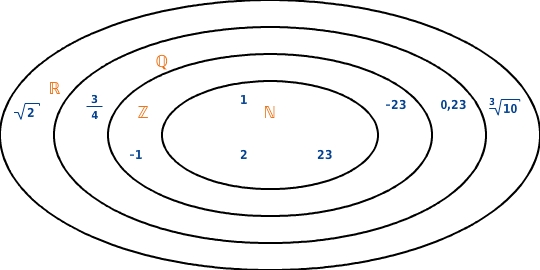Jede natürliche Zahl ist eine ganze Zahl.
Jede ganze Zahl ist eine rationale Zahl.
Jede rationale Zahl ist eine reelle Zahl.
Jede natürliche Zahl ist eine ganze Zahl.
Jede ganze Zahl ist eine rationale Zahl.
Jede rationale Zahl ist eine reelle Zahl.
Beweis der Irrationalität
Ob das Ergebnis einer Rechnung eine irrationale Zahl ist, kannst du nicht mit dem Taschenrechner entscheiden, da er nur eine begrenzte Anzahl an Stellen nach dem Komma anzeigen kann. Das Ergebnis wird gerundet.
Die Quadratwurzel einer natürlichen Zahl ist irrational, wenn in deren Primfaktorzerlegung mindestens einer der Primfaktoren in ungerader Anzahl vorkommt.Insbesondere ist die Quadratwurzel einer Primzahl stets irrational. Der Beweis wird meist indirekt geführt, hier zum Beispiel für 2.
Es gibt also einen Widerspruch zu der Annahme, dass
nicht gekürzt werden kann! Die Annahme, dass
rational wäre, ist demnach falsch. Dann kann
nur irrational sein.