Grundlagen zur Volumen- und Oberflächenberechnung
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du die Größe zweier rechtwinkliger Körper messen und vergleichen kannst.
Den Rauminhalt eines Körpers bestimmen
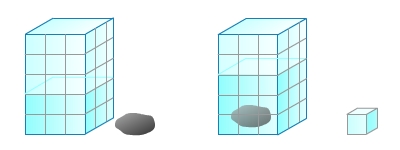
Jeder Körper benötigt Platz. Die Größe dieses Raumes ( den Rauminhalt oder das Volumen) kannst du auf unterschiedliche Weise messen. Rechtwinklige Körper kannst du oft mit Würfeln ausfüllen. Damit man die gemessenen Größen miteinander vergleichen kann, verwendet man Einheitswürfel (eine Kantenlänge entspricht einer Längeneinheit). Der Körper, in den mehr Einheitswürfel passen, hat das größere Volumen.
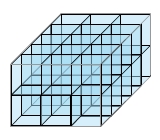
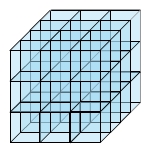
Das Volumen unregelmäßiger oder runder Körper kannst du nicht durch Zählen von Einheitswürfeln bestimmen.Das Volumen eines Hohlkörpers kannst du aber mit Hilfe eines Messbechers bestimmen.
In welche Vase passt mehr Wasser?
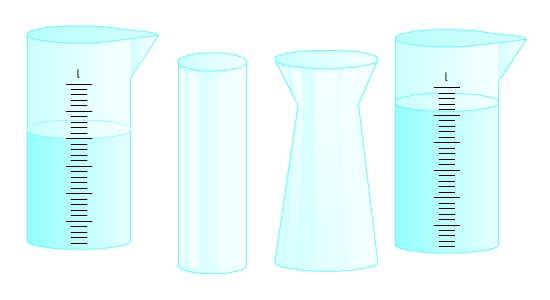
Wenn der Körper nicht hohl ist - also sich nicht füllen lässt - dann gibt es noch eine weitere Möglichkeit sein Volumen zu bestimmen. Du tauchst den Körper (zum Beispiel einen Stein) in ein Gefäß mit Wasser ein und misst, wie stark der Wasserspiegel in dem Gefäß steigt.
Die Oberfläche eines Körpers bestimmen
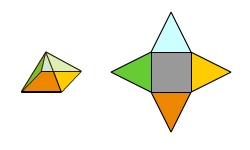
Die Oberfläche (oder auch der Oberflächeninhalt) eines Körpers ist die Summe der Flächeninhalte aller Teilflächen.
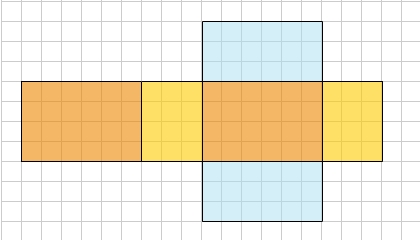
Manche Körper lassen sich an den Kanten so aufschneiden, dass du ein zusammenhängendes Netz der Körperflächen erhältst.
Die Oberfläche des Quaders
Die Oberfläche des Quaders besteht aus sechs Rechtecken. Addierst du die Flächeninhalte dieser sechs Rechtecke, so erhältst du den Oberflächeninhalt des Quaders.
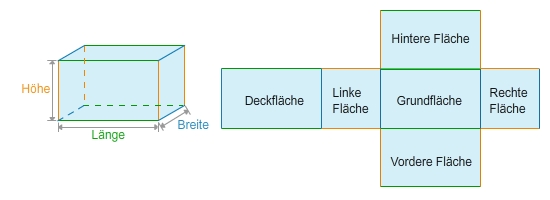
Das Quadernetz ist eine ebene Figur. Du kannst ihren Flächeninhalt bestimmen, indem du die Fläche mit auslegst.