Grundlagen zur Flächen- und Umfangsberechnung
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du die Größe zweier Flächeninhalte oder den Umfang zweier Figuren miteinander vergleichen kannst.
Die Flächeninhalte zweier Figuren vergleichen
Jede gradlinig begrenzte ebene Figur schließt eine bestimmte Fläche ein.Die Größe dieser Fläche gibt man mit dem Flächeninhalt an, zum Beispiel als Anzahl von Kästchen in einem Kästchennetz.Bei manchen Flächen lässt sich leicht sagen, welche der beiden Figuren den größeren Flächeninhalt hat.
Hier ist leicht zu erkennen, dass die rechte Fläche größer ist.
Sind die Größen der beiden Flächen jedoch sehr ähnlich, wird es schwierig zu entscheiden, welche die größere Fläche ist.
Ist hier die linke oder die rechte Fläche größer?
Du hast verschiedene Möglichkeiten herauszufinden, welche der beiden Flächen größer ist.
Durch übereinanderlegen der Flächen Du schneidest eine der Flächen aus und zerlegst sie nötigenfalls in kleinere Teilflächen, um damit die andere Fläche auszulegen.
Da nach dem vollständigen Auslegen der gelben Fläche noch ein Teilstück der blauen Fläche übrig bleibt, hat die blaue Fläche den größeren Flächeninhalt.
Durch Auslegen Du legst die Flächen mit gleich großen Quadraten aus oder unterlegst sie mit einem Kästchennetz.
Die blaue Fläche ist mit 28 ganzen und 8 halben Einheitsquadraten (Dreiecken) ausgelegt. Das macht zusammen: 32 Einheitsquadrate. Die gelbe Fläche ist mit 24 ganzen Einheitsquadraten und 8 halben Einheitsquadraten (Dreiecken) ausgelegt. Das macht zusammen: 28 Einheitsquadrate. Daran siehst du, dass die blaue Figur den größeren Flächeninhalt hat.
Die Umfänge zweier Figuren vergleichen
Jede gradlinig begrenzte ebene Figur hat einen Rand. Die Länge dieses Randes bezeichnet man als den Umfang der Figur.Du erhältst diese Länge, indem du die Längen aller Randstrecken der Figur addierst.
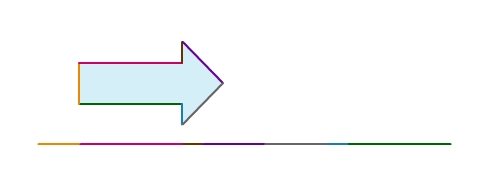
Die Seiten dieser Figur sind in unterschiedlichen Farben markiert. Darunter kannst du sehen, wie lang der Umfang dieser Figur ist. Dazu wurden alle Seiten aneinandergelegt.
Wie würdest du hier entscheiden, welche Figur den größeren Umfang hat?
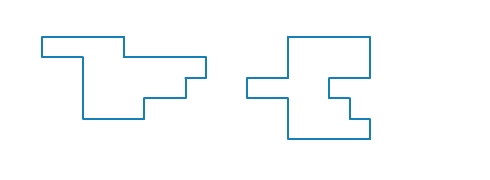
Willst du die Umfänge zweier Flächen miteinander vergleichen, so ist auch hier die Einteilung der Figur in hilfreich.
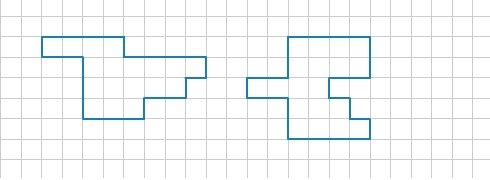
Mit der Längeneinheit „1 Kästchenlänge“ kannst du die Längen der einzelnen Seiten genau auszählen. Die linke Figur hat einen Umfang von Kästchenlängen. Die rechte Figur hat einen Umfang von Kästchenlängen. Damit hat die rechte Figur den größeren Umfang.
Beziehung zwischen Umfang und Flächeninhalt
Jede gradlinig begrenzte ebene Figur hat einen Umfang und einen Flächeninhalt. Haben Figuren mit dem gleichen Umfang auch immer den gleichen Flächeninhalt?Lege zwei verschiedene Figuren mit je zehn solcher Stäbe 
und vergleiche die Flächeninhalte.
und vergleiche die Flächeninhalte.
An diesem Beispiel kannst du erkennen, dass mit der gleichen Anzahl Stäbe einen unterschiedlich große Fläche eingeschlossen werden kann.
Zwei Figuren mit demselben Umfang können also unterschiedliche Flächeninhalte haben.
und vergleiche die Umfänge.
An diesem Beispiel kannst du erkennen, dass mit der gleichen Anzahl Quadrate Figuren unterschiedlichen Umfangs gebildet werden können.
Zwei Figuren mit demselben Flächeninhalt können also unterschiedliche Umfänge haben.
