Graphentheorie
Die Graphen der Graphentheorie haben nichts zu tun mit den Funktionsgraphen der Analysis. Hier handelt es sich hier um Konfigurationen, die aus Punkten, den Knoten, und Kurven, den Kanten, bestehen. Eine Kante verbindet immer zwei Knoten, die auch zusammenfallen dürfenman hat dann eine Schlinge. Zwei Knoten können durch mehrere Kanten verbunden werden. Da es nicht auf die Form der Kurven ankommt, werden die Kanten meist als Verbindungsstrecken gezeichnet, eine Schlinge wird als Kreis gezeichnet. Graphen werden verwendet, um beispielsweise ein Straßennetz mathematisch zu modellieren. Manchmal kommt es auch auf die Richtung der Kanten an (Einbahnstraßen im Straßennetz). Die Kanten werden dann als Pfeile gezeichnet und man erhält einen gerichteten Graphen.
Das älteste Beispiel für die Verwendung von Graphen ist das Königsberger Brücken-Problem.
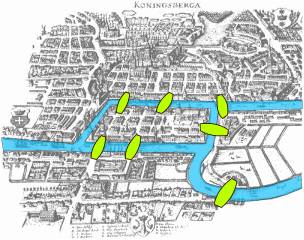
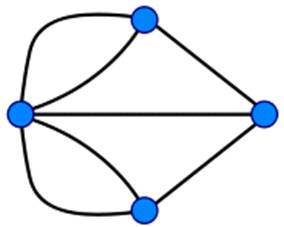
Man soll eine Rundgang durch Königsberg machen und dabei alle 7 Brücken genau einmal überschreiten. Leonhard Euler hat 1735 gezeigt, dass dies nicht möglich ist. Dabei hat er noch von den tatsächlichen Gegebenheiten (des Stadtplans oben links) abstrahiert und die Brücken als Kanten eines Graphen dargestellt sowie als Knoten die Stadtteile gewählt, die durch diese verbunden werden. Man erhält dann die Konfiguration oben rechts. Man sieht, dass von jedem Knoten eine ungerade Anzahl Kanten ausgehen, vom linken Knoten 5, von allen Anderen jeweils 3. Auch wenn man nicht auf einem Rundweg beharrt, d.h. nach der Wanderung zum Ausgangspunkt zurückkehrt, ist eine solche Stadtwanderung nicht möglich. Der Graph darf höchstens zwei Knoten mit einer ungeraden Anzahl Kanten enthalten. Diese können dann als Start- oder Zielknoten dienen, jeden anderen Knoten muss man wieder verlassen können, wenn man ihn erreicht hat.
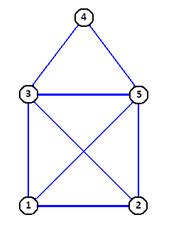 Dem gegenüber hat das bekannte Kinderspiel, das Haus des Nikolaus in einem Zug zu zeichnen stets eine Lösung (ein möglicher Weg ist 1-2-3-4-5-3-1-5-2). Dabei ist es erlaubt jeden Knoten mehrfach zu treffen. Ein anderes Problem wurde 1857 durch William Rowan Hamilton gestellt, nämlich zu entscheiden, ob es in einem gegebenen Graphen, stets einen geschlossenen Weg gibt, bei dem jede Kante und jeder Knoten nur einmal durchlaufen werden.
Dem gegenüber hat das bekannte Kinderspiel, das Haus des Nikolaus in einem Zug zu zeichnen stets eine Lösung (ein möglicher Weg ist 1-2-3-4-5-3-1-5-2). Dabei ist es erlaubt jeden Knoten mehrfach zu treffen. Ein anderes Problem wurde 1857 durch William Rowan Hamilton gestellt, nämlich zu entscheiden, ob es in einem gegebenen Graphen, stets einen geschlossenen Weg gibt, bei dem jede Kante und jeder Knoten nur einmal durchlaufen werden.
Die Graphentheorie wurde auch bei der Lösung eines lange Zeit offenen Problems angewandt, dem Vier-Farben-Problem: Ist es möglich jede vorgegebene Landkarte mit höchstens vier Farben so zu Färben, dass keine beiden aneinander grenzenden Länder dieselbe Farbe besitzen. Das Problem wurde 1852 zum ersten Mal formuliert und konnte erst 1976 von Kenneth Appel und Wolfgang Haken mit Hilfe des Computers positiv beantwortet werden.
Solche Probleme werden heute im Rahmen der Komplexitätstheorie untersucht. Dabei stellt sich die Frage, ob ein Problem mit Hilfe eines Algorithmus gelöst werden kann, wobei die Rechenzeit nicht exponentiell mit der Komplexität des Problems, im Fall eines Graphen mit der Anzahl Knoten und Kanten zunimmt.
Eine praktische Anwendung bietet das Problem des Handlungsreisenden. Dabei wird nach dem kürzesten Weg gesucht, auf dem der Handlungsreisende eine vorgegebene Anzahl von Städten besuchen soll. Bei der mathematischen Modellierung wird dazu ein Graph mit gewichteten Kanten verwendet; die Gewichte stellen ein Maß für die Länge der jeweiligen Verbindungsstrecke dar. Dieses Problem wird mit Methoden der diskreten Optimierung behandelt. Es hat stets eine Lösung, da es bei endlich vielen Städten auch nur endlich viele Wege gibt, unter denen der kürzeste zu bestimmen. Um alle Möglichkeiten durchzurechnen, kann die Rechenkapazität eines Computers aber schnell überschritten werden.

