Gleichsetzungsverfahren zum Lösen linearer Gleichungssysteme
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit dem Gleichsetzungsverfahren lineare Gleichungssysteme mit zwei Variablen lösen kannst.
Lösen von linearen Gleichungssystemen
Du kannst zum Lösen von Gleichungssystemen mit zwei linearen Gleichungen das Gleichsetzungsverfahren nutzen. Ziel dieses Verfahrens ist, eine Gleichung zu erhalten, die nur noch eine Variable enthält.
Wenn bei beiden Gleichungen auf der einen Seite der Gleichung nur die gleiche Variable steht, kannst du die beiden Terme auf der anderen Seite der Gleichung gleichsetzen. Löse folgendes Gleichungssystem in ℚ: 
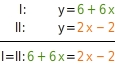
Terme gleichsetzen
Auf der linken Seite steht jeweils nur . Du setzt die Terme und gleich. Du erhältst eine neue Gleichung mit nur einer Variablen ( ).
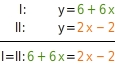
Anzahl der Lösungen bestimmen
Du löst die Gleichung nach auf:  Das Gleichungssystem hat genau eine Lösung, da du für x einen eindeutigen Wert erhältst.
Das Gleichungssystem hat genau eine Lösung, da du für x einen eindeutigen Wert erhältst.

Wie viele Lösungen hat das Gleichungssystem in ℚ? 

Lösungen berechnen
Du hast x bereits im vorigen Schritt berechnet. Um y zu berechnen, setzt du in eine der Ausgangsgleichungen ein:  Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.
Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis. 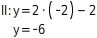

= -2 und = -6
Lösungsmenge bestimmen
Die Lösungsmenge besteht aus dem Zahlenpaar und . Du schreibst die Lösung (in runden Klammern) als Zahlenpaar . Du schreibst für die Lösungsmenge kurz .
L = { -2 ; -6 }
Wenn bei beiden Gleichungen auf der einen Seite der Gleichung nur das gleiche Vielfache einer Variablen steht, kannst du die beiden Terme auf der anderen Seite der Gleichung gleichsetzen. Löse folgendes Gleichungssystem in ℚ: 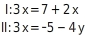

Terme gleichsetzen
Auf der linken Seite steht jeweils nur . Du setzt die Terme und gleich. Du erhältst eine neue Gleichung mit nur einer Variablen (y).

Anzahl der Lösungen bestimmen
Du löst die Gleichung nach y auf: 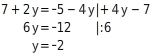 Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutig bestimmten Wert erhältst.
Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutig bestimmten Wert erhältst.
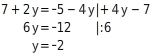
Wie viele Lösungen hat das Gleichungssystem in ℚ? 

Lösungen berechnen
Du hast y bereits im vorigen Schritt berechnet. Um x zu berechnen, setzt du in eine der Ausgangsgleichungen ein: Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.
Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.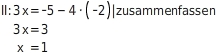

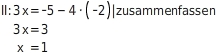
x = 1 und y = -2
Lösungsmenge bestimmen
Die Lösungsmenge besteht aus dem Zahlenpaar und . Du schreibst die Lösung (in runden Klammern) als Zahlenpaar . Du schreibst für die Lösungsmenge kurz .
L = { 1 ; -2 }
Manchmal ist es nötig, eine der Gleichungen erst umzustellen. Löse folgendes Gleichungssystem in ℚ: 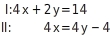
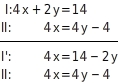

Gleichung umstellen
Du stellst Gleichung I nach um. In Gleichung II steht der Term bereits allein auf der linken Seite. 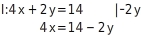
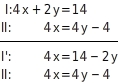
Terme gleichsetzen
Du setzt die Terme und gleich. Du erhältst eine neue Gleichung mit nur einer Variablen (y).

Anzahl der Lösungen bestimmen
Du löst die Gleichung nach auf:  Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutig bestimmten Wert erhältst.
Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutig bestimmten Wert erhältst.

Wie viele Lösungen hat das Gleichungssystem in ℚ? 

Lösungen berechnen
Du hast y bereits im vorigen Schritt berechnet. Um x zu berechnen, setzt du in eine der Ausgangsgleichungen ein: Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.
Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.


x = 2 und y = 3
Lösungsmenge bestimmen
Die Lösungsmenge besteht aus dem Zahlenpaar und . Du schreibst die Lösung (in runden Klammern) als Zahlenpaar . Du schreibst für die Lösungsmenge kurz .
L = { 2 ; 3 }
Anzahl der Lösungen
Bei linearen Gleichungssystemen gibt es drei verschiedene Möglichkeiten für die Anzahl der Lösungen: 
keine Lösung Löse folgendes Gleichungssystem in ℚ: 
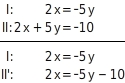

Gleichung umstellen
Du dividierst beide Seiten der Gleichung II durch 2: 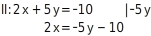
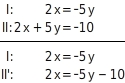
Terme gleichsetzen
Du setzt die Terme und gleich. Du erhältst eine neue Gleichung mit nur einer Variablen (y).

Anzahl der Lösungen bestimmen
Das Gleichungssystem hat keine Lösung, da eine falsche Aussage entsteht: Die Lösungsmenge ist leer: L={ }
Die Lösungsmenge ist leer: L={ }
Wie viele Lösungen hat das Gleichungssystem in ℚ? 

unendlich viele Lösungen Löse folgendes Gleichungssystem in ℚ: 


Gleichung umstellen
Du stellst Gleichung II nach x um: 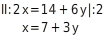

Terme gleichsetzen
Du setzt die Terme und gleich. Du erhältst eine neue Gleichung mit nur einer Variablen (y).

Anzahl der Lösungen bestimmen
Das Gleichungssystem hat unendlich viele Lösungen, da beim Umstellen der Gleichung eine Aussage entsteht, die unabhängig von der Wahl von stets wahr ist: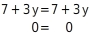 Für jeden -Wert in ℚ erhältst du nach Einsetzen in die Gleichungen genau einen -Wert bzw. für jeden -Wert genau einen -Wert.Durch Umstellen einer der beiden Ausgangsgleichungen erhältst du: Es ergibt sich folgende Lösungsmenge: L = {
Für jeden -Wert in ℚ erhältst du nach Einsetzen in die Gleichungen genau einen -Wert bzw. für jeden -Wert genau einen -Wert.Durch Umstellen einer der beiden Ausgangsgleichungen erhältst du: Es ergibt sich folgende Lösungsmenge: L = { x ; 1 3 x - 7 3 | ∈ ℚ}
Wie viele Lösungen hat das Gleichungssystem in ℚ? 


