Eigenschaften, Oberflächen- und Volumenberechnung von Körpern
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, welche Eigenschaften spezielle geometrische Körper haben, wie du ein Netz und ein Schrägbild eines Körpers zeichnen kannst.Weiter erfährst du, wie du die Oberfläche und das Volumen eines Prismas berechnen kannst.
Eigenschaften von Prisma und Zylinder
Ein Prisma ist ein geometrischer Körper mit: Ein Zylinder ist ein geometrischer Körper mit:
Ein Zylinder ist ein geometrischer Körper mit: HöheDie Höhen von Prisma und Zylinder entsprechen dem Abstand zwischen Grundfläche und Deckfläche.
Ecken, Kanten und FlächenDie Anzahl der Ecken, Kanten und Flächen eines Prismas hängt von der Form der Grundfläche ab. Ein Zylinder hat keine Ecken, zwei Kanten und drei Flächen.
HöheDie Höhen von Prisma und Zylinder entsprechen dem Abstand zwischen Grundfläche und Deckfläche.
Ecken, Kanten und FlächenDie Anzahl der Ecken, Kanten und Flächen eines Prismas hängt von der Form der Grundfläche ab. Ein Zylinder hat keine Ecken, zwei Kanten und drei Flächen.
Schiefes und gerades Prisma
Du kannst zwei Typen von Prismen unterscheiden:Das gerade Prisma: Der Mantel steht senkrecht zur Grundfläche und besteht aus Rechtecken.Das schiefe Prisma: Der Mantel steht nicht senkrecht zur Grundfläche und besteht aus Rechtecken und/oder Parallelogrammen.
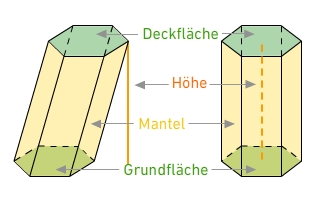

Die Grundfläche und die Deckfläche haben hier die Form eines Sechsecks. Sie sind parallel und gleichgroß.
Quader und Würfel
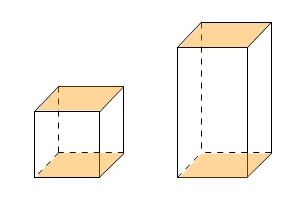

Beim Quader und beim Würfel sind Grundfläche und Deckfläche parallel und gleichgroß. Quader und Würfel sind auch Prismen.
Schiefer und gerader Zylinder
Auch beim Zylinder kannst du zwei Typen unterscheiden: Den geraden Zylinder und den schiefen Zylinder.
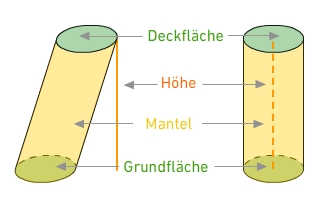

Die Grundfläche und die Deckfläche haben die Form eines Kreises. Sie sind parallel und gleichgroß.
Anzahl der Ecken, Kanten, Flächen eines dreiseitigen Prismas


Dieses Prisma hat sechs Ecken, neun Kanten und fünf Flächen.
Eigenschaften von Pyramide und Kegel
Eine Pyramide ist ein geometrischer Körper mit: Ein Kegel ist ein geometrischer Körper mit:
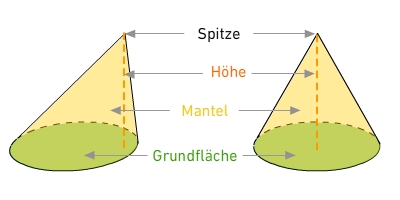
Ein Kegel ist ein geometrischer Körper mit: HöheDie Pyramide und der Kegel haben jeweils eine Höhe. Sie entspricht dem Abstand zwischen der Grundfläche und der Spitze.
Ecken, Kanten und FlächenDie Anzahl der Ecken, Kanten und Flächen eine Pyramide hängt von der Form der Grundfläche ab. Ein Kegel hat zwei Flächen, eine Kante und keine Ecken.
HöheDie Pyramide und der Kegel haben jeweils eine Höhe. Sie entspricht dem Abstand zwischen der Grundfläche und der Spitze.
Ecken, Kanten und FlächenDie Anzahl der Ecken, Kanten und Flächen eine Pyramide hängt von der Form der Grundfläche ab. Ein Kegel hat zwei Flächen, eine Kante und keine Ecken.
 Ein Kegel ist ein geometrischer Körper mit:
Ein Kegel ist ein geometrischer Körper mit: HöheDie Pyramide und der Kegel haben jeweils eine Höhe. Sie entspricht dem Abstand zwischen der Grundfläche und der Spitze.
Ecken, Kanten und FlächenDie Anzahl der Ecken, Kanten und Flächen eine Pyramide hängt von der Form der Grundfläche ab. Ein Kegel hat zwei Flächen, eine Kante und keine Ecken.
HöheDie Pyramide und der Kegel haben jeweils eine Höhe. Sie entspricht dem Abstand zwischen der Grundfläche und der Spitze.
Ecken, Kanten und FlächenDie Anzahl der Ecken, Kanten und Flächen eine Pyramide hängt von der Form der Grundfläche ab. Ein Kegel hat zwei Flächen, eine Kante und keine Ecken.
Pyramide
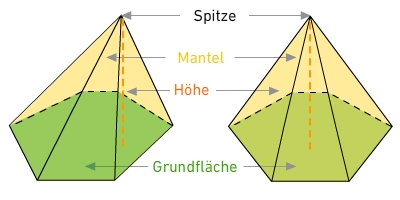

Kegel

Anzahl der Ecken, Kanten, Flächen einer fünfseitigen Pyramide
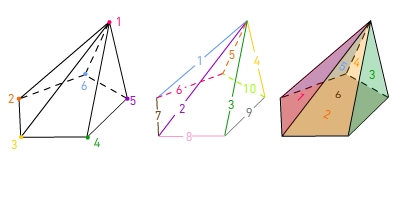

Diese Pyramide hat sechs Ecken, zehn Kanten und sechs Flächen.
Eigenschaften der Kugel
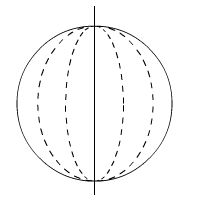
Eine Kugel ist der geometrische Körper, den du erhältst, wenn du einen Kreis um seinen Durchmesser rotieren lässt.Die Kugel hat einen Mittelpunkt.

Abstand Mittelpunkt - Oberfläche
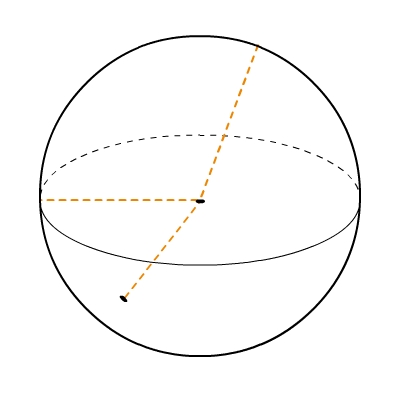

Der Abstand vom Mittelpunkt ist für jeden Punkt der Kugeloberfläche gleich und wird Kugelradius genannt.
Netz eines Körpers
Um ein Netz darzustellen, stelle dir vor, du würdest einen Körper entlang seiner Kanten öffnen und seine aufgeklappten Flächen in eine Ebene legen.Das Netz eines Körpers besteht also aus so vielen Flächenstücken, wie der Körper Flächen hat.
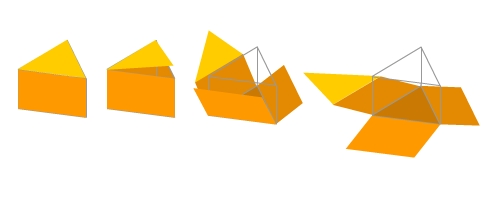 Wenn du das Netz eines Körpers faltest, bilden die Seiten der Flächen die Kanten des Körpers. Also müssen zwei beim Zusammenfalten aufeinandertreffende Seiten gleich lang sein.Häufig kann man von einem Körper mehrere verschiedene Netz abbilden.
Wenn du das Netz eines Körpers faltest, bilden die Seiten der Flächen die Kanten des Körpers. Also müssen zwei beim Zusammenfalten aufeinandertreffende Seiten gleich lang sein.Häufig kann man von einem Körper mehrere verschiedene Netz abbilden.
 Wenn du das Netz eines Körpers faltest, bilden die Seiten der Flächen die Kanten des Körpers. Also müssen zwei beim Zusammenfalten aufeinandertreffende Seiten gleich lang sein.Häufig kann man von einem Körper mehrere verschiedene Netz abbilden.
Wenn du das Netz eines Körpers faltest, bilden die Seiten der Flächen die Kanten des Körpers. Also müssen zwei beim Zusammenfalten aufeinandertreffende Seiten gleich lang sein.Häufig kann man von einem Körper mehrere verschiedene Netz abbilden.
Netz eines geraden dreiseitigen Prismas
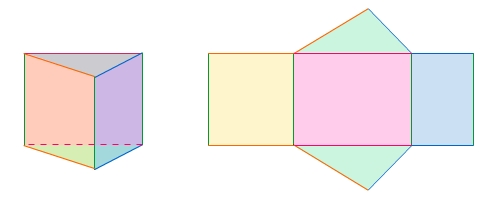

Dieses gerade Prisma mit einem Dreieck als Grundfläche besteht aus zwei Dreiecken (Grund- und Deckfläche) und drei Rechtecken (den Flächen des Mantels). Beim Körper und beim Netz sind gleiche Längen gleichfarbig gekennzeichnet.
Mehrere Netze einer Pyramide mit einem Quadrat als Grundfläche
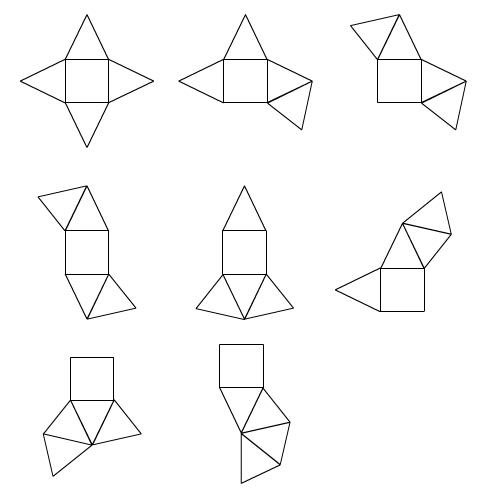

Der Mantel einer geraden Pyramide mit einem Quadrat als Grundfläche setzt sich aus vier Dreiecken zusammen.Es gibt für die quadratische Pyramiden verschiedene Netze.
Netz eines geraden Zylinders mit Höhe8cmund Durchmesser3cm
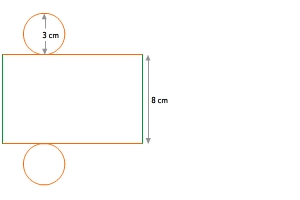

Ein Zylinder setzt sich aus zwei Kreisen (Grund- und Deckfläche) und einem Rechteck (abgerollte Mantelfläche) zusammen. Eine Seite des Rechtecks ist genauso lang wie der Umfang des Kreises, die andere Seite ist genauso lang wie die Höhe des geraden Zylinders.
Netz eines Kegels


Ein Kegel setzt sich aus einem Kreis (Grundfläche) und einem Kreisausschnitt (abgerollte Mantelfläche) zusammen.
Schrägbild
Einen Körper kannst du räumlich zeichnen. Eine solche Zeichnung nennt man Schrägbild. Beim Schrägbild sind folgende Regeln zu beachten:


Schrägbilder eines Prismas, einer Pyramide, eines Zylinder und eines Kegels
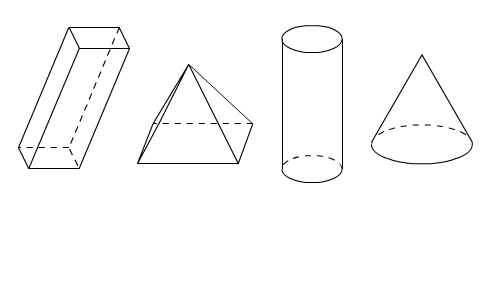
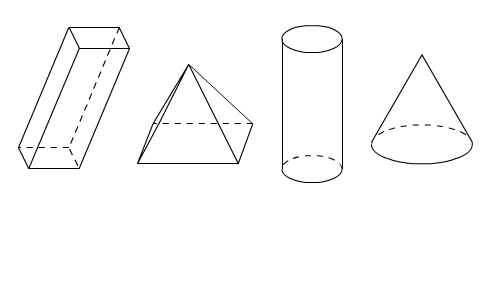
Die Position der gestrichelten Linien ist wichtig.
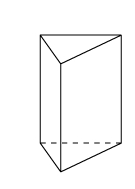
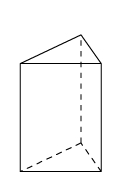


Bei der Figur links kannst du zwei Flächen des Mantels deutlich sehen, die dritte ist verdeckt.Bei der Figur rechts kannst du nur eine Seite des Mantels deutlich sehen, zwei Seiten sind verdeckt.
Kavalierperspektive eines Prismas
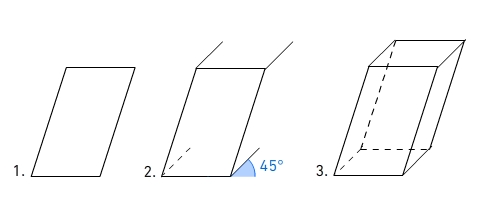
Bei einer Kavalierperspektive werden die Kanten, die senkrecht in die Tiefe verlaufen, um die Hälfte gekürzt und in einem Winkel von
45° dargestellt.
So zeichnest du ein Prisma in Kavalierperspektive.

Oberfläche eines Prismas
Die Oberfläche eines Körpers kannst du berechnen, indem du den Flächeninhalt aller Flächen des Körpers addierst.Beim Prisma sind die Grundfläche und die Deckfläche deckungsgleich. Daher sind ihre Flächeninhalte identisch. Für die Oberfläche eines Prismas addierst du das Doppelte des Flächeninhalts der Grundfläche
AG und den Flächeninhalt des Mantels
AM.
O=2·AG+AM
Oberfläche Prisma:
O=2·AG+AM
Das Netz des Prismas kann dir helfen, die Oberfläche zu berechnen.


Der Flächeninhalt des Netzes ist gleich der Oberfläche des Prismas.
Oberfläche eines Prismas berechnen
Berechne die Oberfläche des geraden dreiseitigen Prismas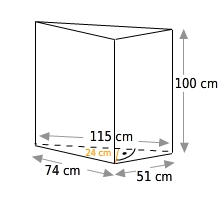

Flächeninhalt der Grundfläche
AG berechnen
Die Grundfläche des Prismas hat die Form eines Dreiecks. Die Formel zur Flächeninhaltsberechnung lautet:
AG=12g·h, wobei g eine Grundseite des Dreiecks bezeichnet und h die zugehörige Höhe.Du setzt die Werte in die Formel ein (
g=115cm und
h=24cm):


AG=1380cm2
Flächeninhalt des Mantels
AM berechnen
Der Mantel des Prismas besteht aus drei Rechtecken, deren Maße jeweils
74cm mal
100cm,
51cm mal
100cm, und
115cm mal
100cm betragen.Der Flächeninhalt des Mantels
AM beträgt also:


AM=24000cm2
Oberfläche O des Prismas berechnen
Die Formel zur Oberflächenberechnung eines Prismas lautet:
O=2·AG+AM Du setzt die Werte in die Formel ein (
AG=1380cm2 und
AM=24000cm2):
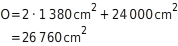
O=26760cm2
Oberfläche eines Prismas berechnen
Berechne die Oberfläche des geraden fünfseitigen Prismas. Die Grundfläche lässt sich in ein Quadrat und ein Trapez zerlegen.

Flächeninhalt der Grundfläche
AG berechnen
Die Grundfläche des Prismas lässt sich in ein Quadrat und in ein Trapez zerlegen.
Der
Flächeninhalt des QuadratsAQbeträgt: Der
Flächeninhalt des TrapezesATbeträgt:
Der
Flächeninhalt des TrapezesATbeträgt: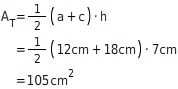 Der
Flächeninhalt der GrundflächeAGbeträgt also:
Der
Flächeninhalt der GrundflächeAGbeträgt also: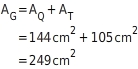
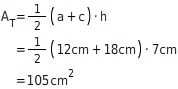 Der
Flächeninhalt der GrundflächeAGbeträgt also:
Der
Flächeninhalt der GrundflächeAGbeträgt also: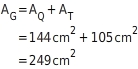
AG=249cm2
Flächeninhalt des Mantels
AM berechnen
Der Mantel des Prismas besteht aus fünf Rechtecken, deren Maße jeweils
12cm mal
30cm,
12cm mal
30cm,
10cm mal
30cm,
18cm mal
30cm und
19cm mal
30cm betragen.Der Flächeninhalt des Mantels
AM beträgt also:


AM=2130cm2
Oberfläche O des Prismas berechnen
Die Formel zur Oberflächenberechnung eines Prismas lautet:
O=2·AG+AM Du setzt die Werte in die Formel ein (
AG=249cm2 und
AM=2130cm2):
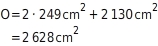
O=2628cm2
Rauminhalt eines Prismas
Das Volumen eines Prismas berechnest du, indem du den Flächeninhalt der Grundfläche
AG mit der Höhe h des Prismas, d. h. dem Abstand von Grund- und Deckfläche, multiplizierst.
V=AG·h
Volumen des Prismas:
V=AG·h
Volumen von Quader und Würfel
Aus der Formel zur Volumenberechnung eines Prismas kannst du die Formel für den Quader und den Würfel ableiten.
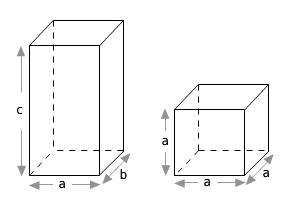

Die Formel zur Volumenberechnung eines Prismas lautet:
V=AG·h
Beim Quader erhältst du: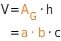 Beim Würfel erhältst du:
Beim Würfel erhältst du:

Volumen eines Prismas berechnen
Berechne das Volumen des Prismas mit einem Parallelogramm als Grundfläche.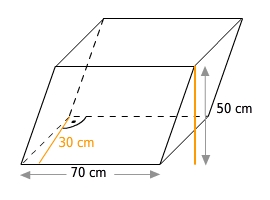

Flächeninhalt der Grundfläche
AG berechnen
Die Grundfläche des Prismas hat die Form eines Parallelogramms (mit der Grundseite g =
70cm und der Höhe
hg=
30cm). Du setzt die Werte in die Formel zur Flächenberechnung eines Parallelogramms ein:


AG=2100cm2
Volumen des Prismas berechnen
Die Formel zur Volumenberechnung eines Prismas lautet:
V=AG·h
Du setzt die Werte in die Formel ein (
AG=2100cm2 und
h=50cm)

V=105000cm3
Volumen eines Prismas mit einem regelmäßigen Fünfeck als Grundfläche berechnen
Berechne das Volumen des Prismas.

Flächeninhalt der Grundfläche
AG berechnen
Die Grundfläche hat die Form eines Fünfecks, das sich in fünf gleichgroße Dreiecke zerlegen lässt.Du kennst die Länge
gD der Grundseite (
15cm) und die zugehörige Höhe
hD(
10.3cm) eines Dreiecks. Daher kannst du den Flächeninhalt
AD eines Dreiecks (in cm?) berechnen:
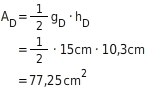 Um den Flächeninhalt
AG des Fünfecks zu berechnen, multiplizierst du den Flächeninhalt eines Dreiecks (
77.25cm2) mit 5:
Um den Flächeninhalt
AG des Fünfecks zu berechnen, multiplizierst du den Flächeninhalt eines Dreiecks (
77.25cm2) mit 5:

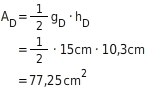 Um den Flächeninhalt
AG des Fünfecks zu berechnen, multiplizierst du den Flächeninhalt eines Dreiecks (
77.25cm2) mit 5:
Um den Flächeninhalt
AG des Fünfecks zu berechnen, multiplizierst du den Flächeninhalt eines Dreiecks (
77.25cm2) mit 5:

AG=330cm2
Volumen des Prismas berechnen
Die Formel zur Volumenberechnung eines Prismas lautet:
V=AG·h
Du setzt die Werte in die Formel ein (
AG=386.25cm2 und
h=20cm)

V=7725cm3

