+49 30 300 2440 00
 – Mo bis Fr von 8:30 - 17 Uhr

Eigenschaften gebrochen-rationaler Funktionen

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, welche Eigenschaften gebrochen-rationale Funktion haben, wie du ihren Definitionsbereich bestimmen und ihren Graphen erkennen kannst.
Außerdem wird dir gezeigt, wie du den Graphen einer Funktion mit der Funktionsgleichung vom Typ y = a x + c + d zeichnen kannst.

Beispiele

Funktionen mit Funktionsgleichungen wie y = 1 x , y = 1 x + 2 + 3 , y = x x - 3 , y = 1 x - 11 2 oder y = 3 x 2 x 5 + 4 heißen gebrochen-rationale Funktionen.
In den Funktionstermen gebrochen-rationaler Funktionen steht das Argument auch im Nenner.
Oft haben gebrochen-rationale Funktionen Definitionslücken, da der Nenner nicht null werden darf.In der Nähe der Definitionslücken zeigen die Graphen der Funktionen ein besonders Verhalten.
Die Graphen gebrochen-rationaler Funktionen vom Typ y = a x + c + d sind Hyperbeln.
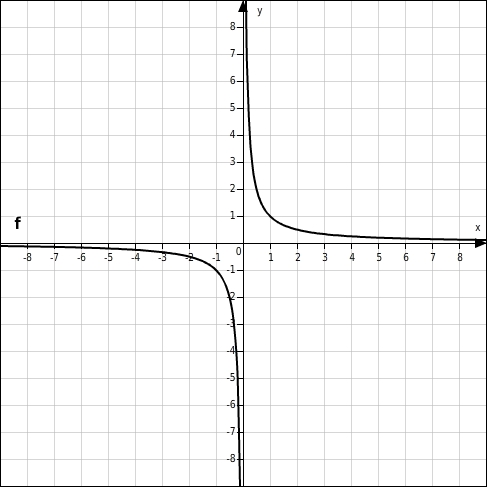
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_1.jpg
Der Graph der gebrochen-rationalen Funktion f mit y = 1 x ist eine Hyperbelund hat eine Definitionslücke bei x = 0 .
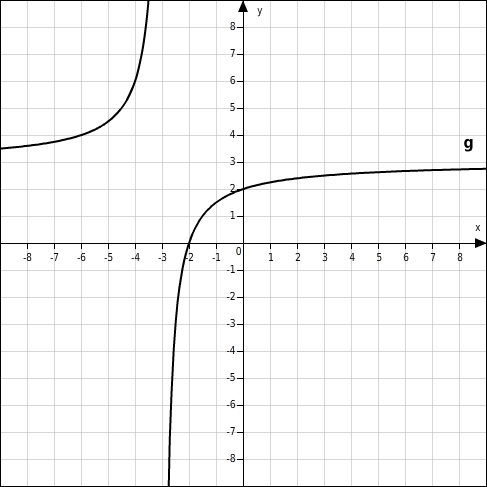
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_2.jpg
Der Graph der gebrochen-rationalen Funktion g mit y = x x + 3 + 2 ist eine Hyperbelund hat eine Definitionslücke bei x = -3 .
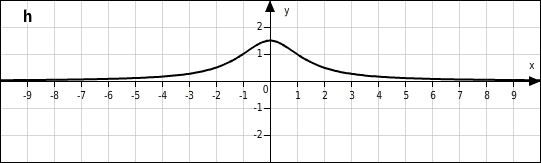
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_3.jpg
Der Graph der gebrochen-rationalen Funktion h mit y = 3 x 2 + 2 ist keine Hyperbelund hat keine Definitionslücke.

Definitionslücken und Definitionsbereiche bestimmen

In den Funktionstermen gebrochen-rationaler Funktionen steht das Argument auch im Nenner.Da nicht durch 0 dividiert werden kann, ist nicht jede gebrochen-rationale Funktion für alle rationalen Zahlen definiert.
Der Definitionsbereich einer Funktion besteht immer aus Zahlen, die als Argument vorkommen können.
Ist allgemein vom Definitionsbereich die Rede, ist immer der maximale Definitionsbereich gemeint, also von der Menge aller Zahlen, für die die Funktion definiert ist.
Hat der Definitionsbereich einer Funktion an der Stelle x L eine Lücke, das heißt, der Funktionswert kann in einer Umgebung für alle x -Werte berechnet werden, aber für x L nicht, dann ist x L eine Definitionslücke der Funktion.
Eine gebrochen-rationale Funktion kann auch mehrere Definitionslücken haben oder gar keine.
Wenn eine Funktion zum Beispiel nur an den Stellen x = -3 und x = 7 Definitionslücken hat, ist der maximale Definitionsbereich in der Grundmenge ℚ:
D = ℚ ∖ -3 , 7 , also die Menge aller rationalen Zahlen ohne -3 und 7.
Bestimme den maximalen Definitionsbereich D in der Grundmenge ℚ für die Funktion f mit f(x) = x x + 5 .
Definitionslücke bestimmen
Du bestimmst die Nullstelle des Nenners. Dazu löst du die Gleichung x + 5 = 0 .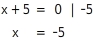
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_4.jpg
Die Funktion hat eine Definitionslücke bei x = -5 .
Definitionsbereich angeben
Der maximale Definitionsbereich besteht aus allen Zahlen aus ℚ ohne -5.
D = ℚ ∖ -5
Bestimme den maximalen Definitionsbereich D in der Grundmenge ℚ für die Funktion g mit g(x) = x x 2 + 6 .
Definitionsbereich bestimmen
Da x 2 + 6 nie null ist ( x 2 ≥ 0 für alle x ∈ ℚ), hat die Funktion keine Definitionslücke.
Die Funktion ist für alle x ∈ ℚ definiert.
D = ℚ
Bestimme den maximalen Definitionsbereich D in der Grundmenge ℚ für die Funktion h mit h(x) = x x + 6 x - 3 .
Definitionsbereich bestimmen
x + 6 x - 3 = 0 für x = -6 und x = 3 Die Funktion hat also zwei Definitionslücken, eine bei x = -6 und eine bei x = 3 .
D = ℚ ∖ -6 , 3

Waagerechte und senkrechte Asymptoten bestimmen

Geraden, denen sich der Graph einer Funktion beliebig nähert ohne sie zu berühren, heißen Asymptoten.
Waagerechte AsymptoteWenn sich für sehr große und sehr kleine x -Werte die Funktionswerte einem Wert c annähern, dann hat der Graph der Funktion eine waagerechte Asymptote mit der Gleichung y = c .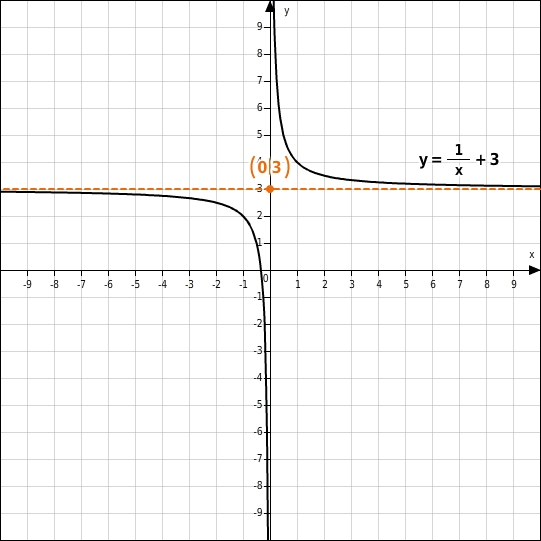
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_5.jpg
Senkrechte AsymptoteWird der Betrag der Funktionswerte beliebig groß, während sich die x -Werte einer Definitionslücke b annähern, dann hat die gebrochen-rationale Funktion eine senkrechte Asymptote mit der Gleichung x = b . b nennt man dann auch Polstelle der Funktion.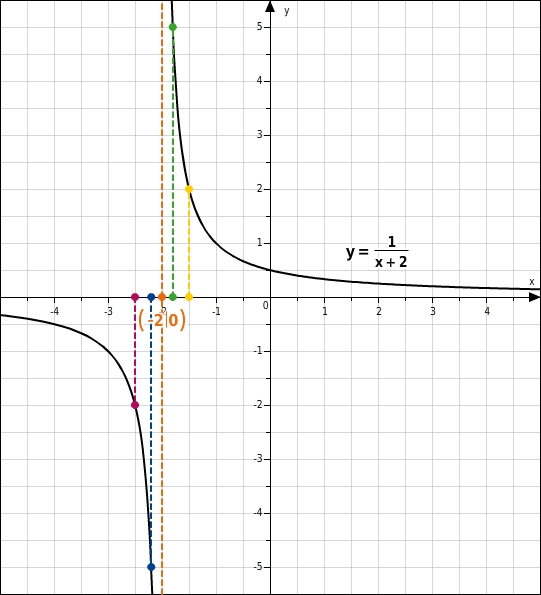
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_6.jpg
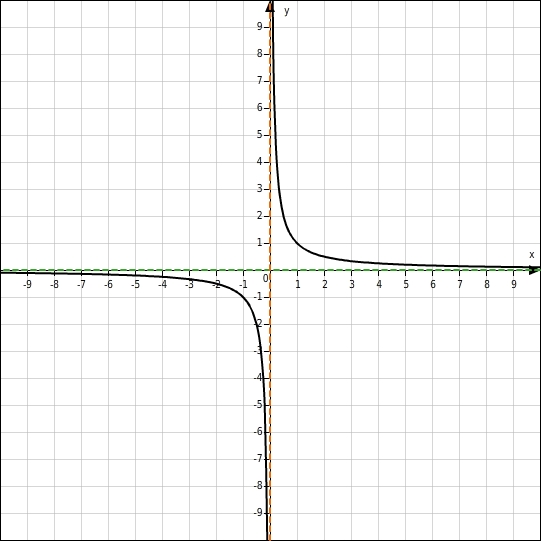
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_7.jpg
Der Graph der Funktion f mit dem Term f(x) = 1 x hat die x -Achse als waagerechte Asymptote und die y -Achse als senkrechte Asymptote.
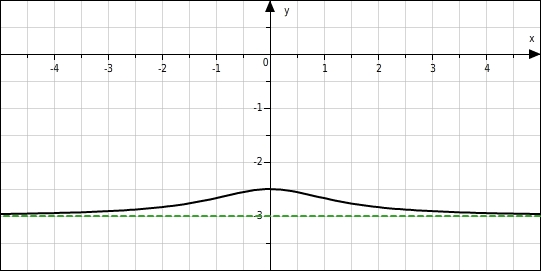
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_8.jpg
Der Graph der Funktion g mit dem Term g(x) = 1 x 2 + 2 - 3 hat eine waagerechte Asymptote aber keine senkrechte Asymptote.
Für sehr große und sehr kleine x -Werte nähern sich die Funktionswerte -3 an.Die Funktion hat keine Definitionslücke, ihr Graph hat keine senkrechte Asymptote.
Hat der Funktionsterm die Form f(x) = x x + c + d , so hat die waagerechte Asymptote die Gleichung y = 1 + d , denn für sehr große und sehr kleine x -Werte nähern sich die Werte des Terms x x + c dem Wert 1 an, da sich Zähler und Nenner immer mehr angleichen.
Gesucht sind die Gleichungen der Asymptoten der Funktion f mit f(x) = x x + 1 + 3
Die Wertetabelle zeigt Funktionswerte für große und kleine x -Werte./wp-content/uploads/media/kem_FuD_FuDEgrFEig_9.jpg
Die Funktionswerte nähern sich dem Wert 4 an, die Gleichung der waagerechten Asymptote ist y = 4 .
f hat eine Definitionslücke bei x = -1 , denn x + 1 = 0 für x = -1 .Die Wertetabelle zeigt Funktionswerte in der Nähe der Definitionslücke.
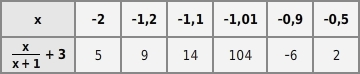/wp-content/uploads/media/kem_FuD_FuDEgrFEig_10.jpg
Die Funktionswerte werden in der Nähe der Definitionslücke sehr groß bzw. sehr klein. Die Definitionslücke ist also eine Polstelle und die Gleichung der senkrechten Asymptote ist x = -1 .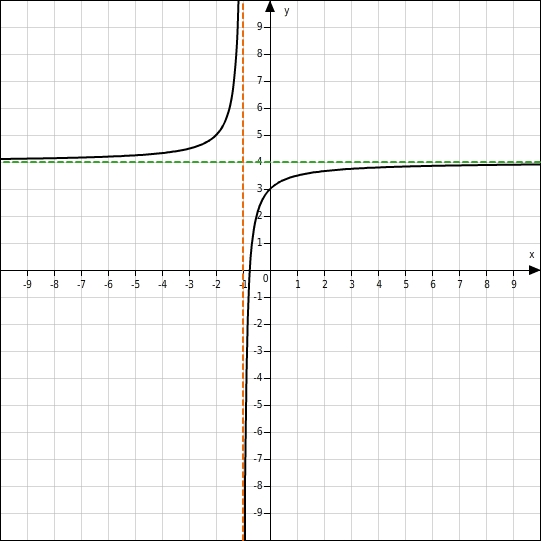
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_11.jpg

Einfluss von Parametern auf den Graphen der Funktion

Für die drei Funktionen f , g und h mit f(x) = a x , g(x) = a x + c und h(x) = a x + d gilt:
g(x) = f(x+c) und h(x) = f(x) + d
Wenn du den Graphen zur Funktionsgleichung y = a x bereits kennst, erhältst du durch Verschieben im Koordinatensystem auch den Graphen zur Gleichung y = a x + c + d , denn die Form des Graphen ändert sich durch die Parameter c und d nicht.
Einfluss des Parameters c : Wenn eine Zahl c zum Argument x addiert wird, dann verschiebt sich der Graph der Funktion parallel zur x -Achse, für c < 0 nach rechts, für c > 0 nach links.
Den Graphen der Funktion mit Funktionsgleichung y = a x + c bzw. y = a x - c erhältst du also, indem du den Graphen zu y = a x um c Einheiten nach links bzw. nach rechts verschiebst.
Gegeben ist die Funktion f mit f(x) = 8 x . Durch welche Verschiebung des Graphen von f entsteht der Graph der Funktion g mit g(x) = 8 x - 2 ?
Verschiebung bestimmen
Du kannst die Verschiebung rechnerisch überprüfen:
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_12.jpg
Zwei Funktionswerte von f und g stimmen dann überein, wenn das Argument von g um 2 größer ist als das Argument von f .
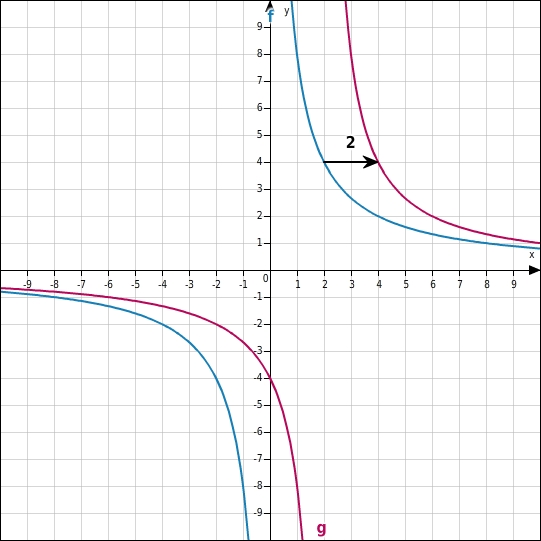
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_13.jpg
Der Graph von g entsteht durch eine Verschiebung des Graphen von f um 2 Einheiten nach rechts.
Einfluss des Parameters d Wenn eine Zahl d zum Funktionswert f(x) addiert wird, dann verschiebt sich der Graph der Funktion parallel zur y -Achse, für d < 0 nach unten, für d > 0 nach oben.
Den Graphen der Funktion mit der Gleichung y = a x + d , bzw. y = a x - d erhältst du also, indem du den Graphen zu y = a x um d Einheiten nach oben bzw. nach unten verschiebst.
Gegeben ist die Funktion f mit f(x) = 8 x . Durch welche Verschiebung des Graphen von f entsteht der Graph der Funktion h mit h(x) = 8 x + 3 ?
Verschiebung bestimmen
Du kannst die Verschiebung rechnerisch überprüfen: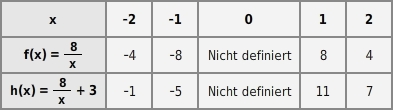
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_14.jpg
Für alle Funktionswerte von f und h gilt: h(x) = f(x) + 3 .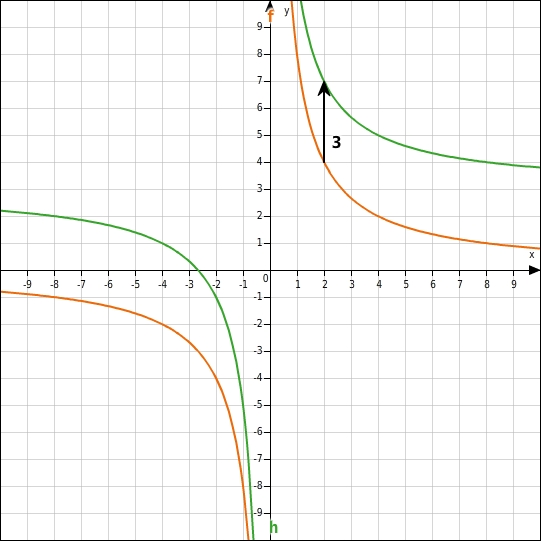
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_15.jpg
Der Graph von h entsteht durch eine Verschiebung des Graphen von f um 3 Einheiten nach oben.
Die Funktionsgleichung kann auch beide Parameter gleichzeitig enthalten. Der Graph zu y = a x wird dann entlang beider Achsen verschoben:
Gegeben ist die Funktion f mit f(x) = 8 x . Durch welche Verschiebung des Graphen von f entsteht der Graphder Funktion g mit g(x) = 8 x - 2 - 4 ?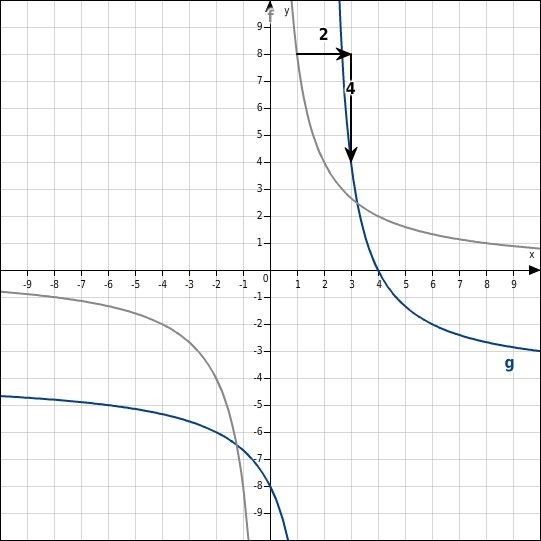
Verschiebung bestimmen
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_16.jpg
Der Graph von g entsteht durch eine Verschiebung des Graphen von f um 2 Einheiten nach rechts und 4 Einheiten nach unten.

Graphen und Funktionsterme

Bei der Zuordnung von Funktionsgleichungen oder Funktionstermen zu ihren Graphen, kannst du dich an der Existenz von Asymptoten, der Anzahl der Polstellen oder der Lage des Graphen im Koordinatensystem orientieren.
Gegeben sind die Graphen der Funktionen f und g .Ordne den Graphen die Terme 2 x - 1 + 3 und 2 x + 3 - 1 richtig zu.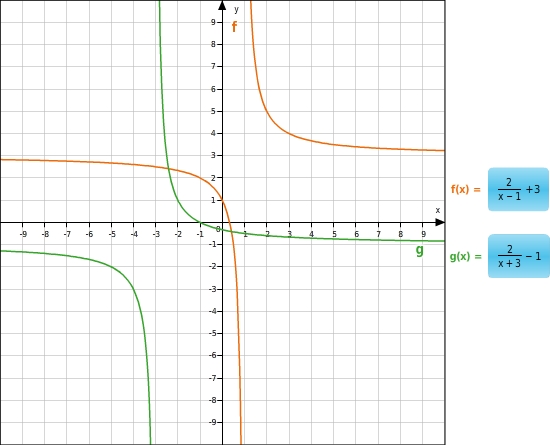
Graphen zuordnen
Du untersuchst die Graphen auf Asymptoten und vergleichst sie mit den Definitionslücken und Termwerten für große bzw. kleine x -Werte der beiden Terme.
Der Graph der Funktion f hat eine senkrechte Asymptote bei x = 1 und eine waagerechte Asymptote bei y = 3 .Dazu gehört der Term 2 x - 1 + 3 mit der Definitionslücke bei x = 1 .
Der Graph der Funktion g hat eine senkrechte Asymptote bei x = -3 und eine waagerechte Asymptote bei y = -1 .Dazu gehört der Term 2 x + 3 - 1 mit der Definitionslücke bei x = -3 .Bei beiden Termen nähern sich die Termwerte für große bzw. kleine x -Werte dem jeweiligen Wert des Absolutgliedes (3 bzw. -1) an.
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_17.jpg
Gegeben sind die Graphen der Funktionen f , g und h . Ordne den Graphen die Terme 3 x 2 + 1 , 3 x + 1 2 und 3 x 2 - 1 richtig zu.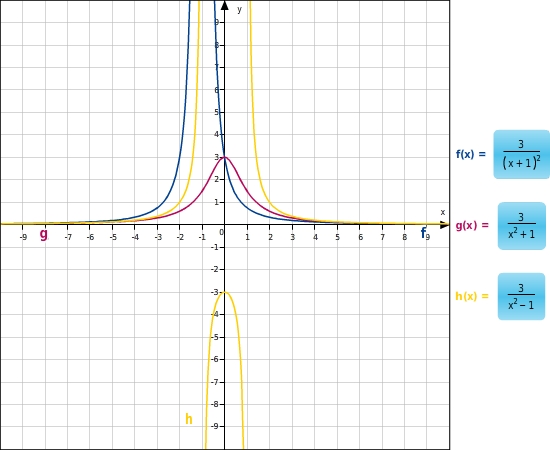
Graphen zuordnen
Die Graphen von f und g verlaufen oberhalb der x -Achse. Die Funktionswerte von f und g sind also immer positiv.Die Termwerte der Terme 3 x 2 + 1 und 3 x + 1 2 sind auch für alle x des jeweiligen Definitionsbereiches positiv.
3 x 2 + 1 hat keine Definitionslücke, also hat der zugehörige Graph keine senkrechte Asymptote.
3 x + 1 2 hat eine Polstelle bei x = -1 , also der zugehörige Graph eine senkrechte Asymptote.
3 x 2 - 1 hat zwei Definitionslücken, da x 2 - 1 = 0 für x = 1 und für x = -1 , die auch Polstellen sind.Also hat der zugehörige Graph zwei senkechte Asymptoten.
/wp-content/uploads/media/kem_FuD_FuDEgrFEig_18.jpg