Zwei sind , wenn du sie so übereinander legen kannst, dass sie passgenau aufeinander liegen.
Du kannst dann eine Figur durch an einer Achse, oder auf die andere .
Hier siehst du für ein Dreieck 1 ein gespiegeltes Dreieck 2, dieses verschoben zum Dreieck 3 und weiter gedreht zum Dreieck 4.
Alle vier Dreiecke sind zueinander kongruent.
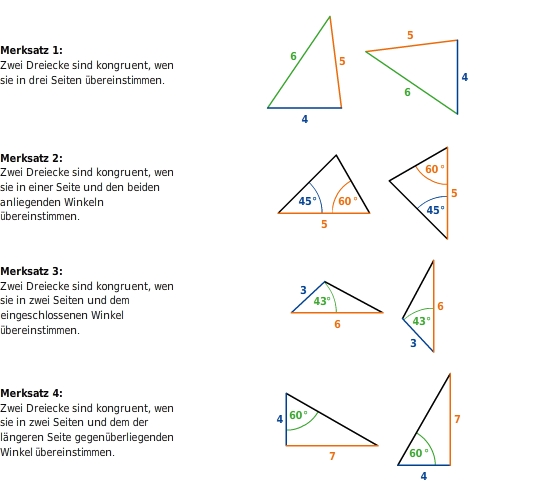
Es gibt vier Kongruenzsätze für Dreiecke.
Konstruktionen mit Kongruenzsätzen
Du kannst ein konstruieren, wenn die gegebenen Stücke einen der Kongruenzsätze erfüllen und die Seitenlängen die erfüllen.
Denn dann sind alle Dreiecke, die du mit den gegebenen Stücken konstruieren kannst zueinander kongruent.
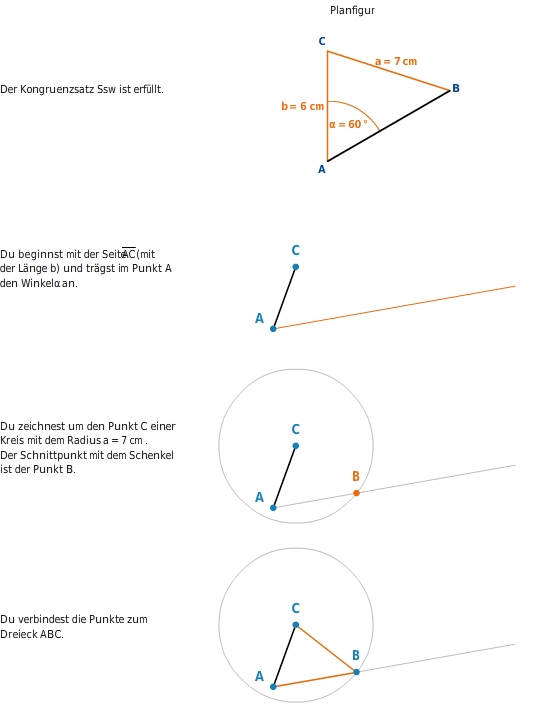
Bevor du mit der Konstruktion beginnst, zeichnest du dir eine Planfigur, in der du die gegebenen Stücke farbig hervorhebst. Achte dabei auf die richtige Beschriftung.
Sind drei Seitenlängen gegeben (sss), überprüfst du zuerst, ob die Dreiecksungleichung erfüllt ist.
Dreieck ABC mit , und
Konstruierbarkeit von Dreiecken und Sonderfälle
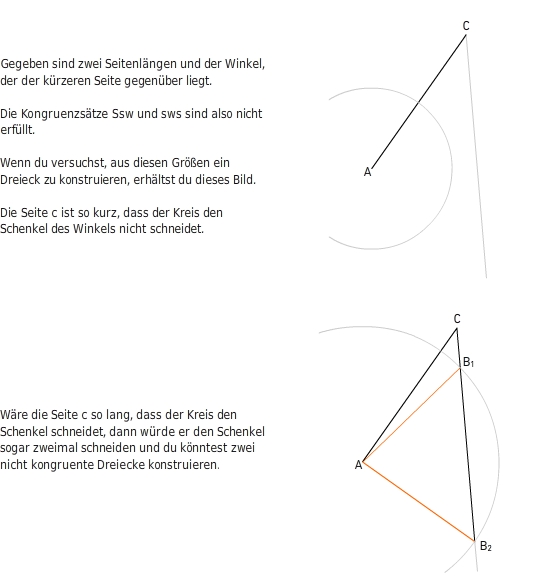
Hast du nur zwei Größen gegeben, oder drei Größen, die zu keinem Kongruenzsatz passen, dann kannst du entweder gar kein , zwei verschiedene Dreiecke oder unendlich viele verschiedene Dreiecke konstruieren.
Die Konstruktion ist dann nicht eindeutig, wenn
• zwei Seitenlängen gegeben sind,
• eine Seitenlänge und ein gegeben sind,
• drei Winkel gegeben sind.
Im letzten Fall muss die betragen.
Dreieck ABC mit , und
Erfolgreich Mathe lernen mit bettermarks
Mit den adaptiven Mathebüchern von bettermarks können Schüler Aufgaben auf dem Tablet, dem Computer und dem Smartphone rechnen.
Wirkung wissenschaftlich bewiesen
Die Regierung von Uruguay hat eine dreijährige Studie auf Basis von UNESCO-Daten zur Nutzung von bettermarks durchgeführt. Das Ergebnis: Bis zu 30% Lernzuwachs.
Über 100 Millionen gerechnete Aufgaben pro Jahr
Jeden Monat rechnen über 100.000 Schülerinnen und Schüler mit bettermarks. Dabei werden mehr als 100 Millionen Aufgaben pro Jahr gelöst.
In Schulen in über zehn Ländern weltweit im Einsatz
bettermarks ist in vier Sprachen verfügbar und wird unter anderem in Deutschland, den Niederlanden, Uruguay und Südafrika täglich im Unterricht eingesetzt.
