Die Winkelfunktionen Sinus und Kosinus
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenVom Einheitskreis zur Winkelfunktion
Die Bezeichnung „Sinus“ ist lateinisch und bedeutet Bogen.
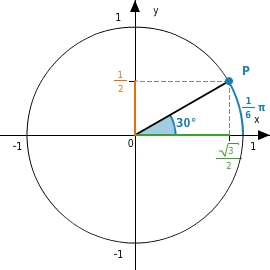
Bewegst du einen Punkt P auf dem Einheitskreis gegen den Uhrzeigersinn und trägst zu jedem Drehwinkel
die y-Koordinate des Punktes P in ein Koordinatensystem ein, erhältst du den Graphen der Sinusfunktion sin:
 Trägst du die x-Koordinate ein, erhältst du den Graphen der Kosinusfunktion cos:
Trägst du die x-Koordinate ein, erhältst du den Graphen der Kosinusfunktion cos:
 Beachte aber: Es ist üblich, für das Argument einer Funktion die Variable x zu verwenden.
Zu einem Winkel
(in Grad oder Bogenmaß) gehört dann ein Punkt
auf dem Einheitskreis mit den Koordinaten
Beachte aber: Es ist üblich, für das Argument einer Funktion die Variable x zu verwenden.
Zu einem Winkel
(in Grad oder Bogenmaß) gehört dann ein Punkt
auf dem Einheitskreis mit den Koordinaten cos α | sin α und je ein Punkt auf den Graphen der Sinus- bzw. Kosinusfunktion:
) und
.
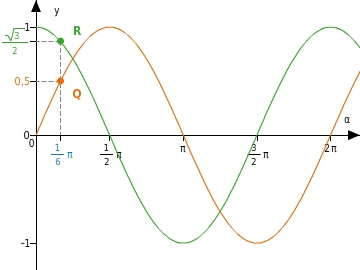


Der Graph der Sinusfunktion
Der Graph der Sinusfunktion lässt sich sowohl für Argumente im Gradmaß als auch im Bogenmaß zeichnen.
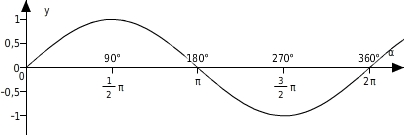

Eigenschaften der Sinusfunktion
Die Sinusfunktion Im Intervall
Im Intervall 0 ; 360 ° bzw. 0 ; 2 π gilt: die Sinusfunktion Der Graph hat im Intervall
Der Graph hat im Intervall 0 ; 360 ° bzw. 0 ; 2 π 
 Im Intervall
Im Intervall  Der Graph hat im Intervall
Der Graph hat im Intervall 
Der Graph der Kosinusfunktion
Der Graph der Kosinusfunktion lässt sich sowohl für Argumente im Gradmaß als auch im Bogenmaß zeichnen.
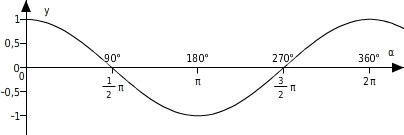

Eigenschaften der Kosinusfunktion
Die Kosinusfunktion Im Intervall
Im Intervall 0 ; 360 ° bzw. 0 ; 2 π gilt: die Kosinusfunktion Der Graph hat im Intervall
Der Graph hat im Intervall 0 ; 360 ° bzw. 0 ; 2 π 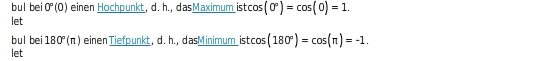
 Im Intervall
Im Intervall  Der Graph hat im Intervall
Der Graph hat im Intervall 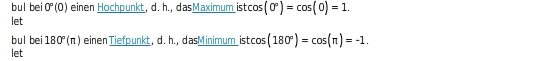
Periodizität
Die Winkelfunktionen sind periodisch. Das heißt, die Funktionswerte wiederholen sich in regelmäßigen Abständen.
Eine periodische Funktion erkennst du am regelmäßigen Verlauf ihres Graphen.
Ist eine Funktion
periodisch, dann gibt es eine kleinste positive reelle Zahl
so, dass für alle ganzen Zahlen
gilt:
. Die Zahl
wird dann die Periode der Funktion
genannt.
du den Graphen der Funktion
um den Wert
entlang der x-Achse nach rechts oder links, fällt der verschobene Graph mit dem ursprünglichen zusammen.
Für die Winkelfunktionen ist die Periode
. Für die Funktionswerte heißt das:
Für alle reellen Zahlen x gilt:
.


Symmetrien von Sinus und Kosinus
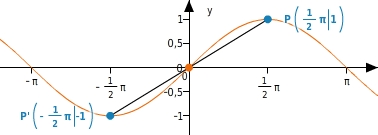
Die Sinusfunktion ist eine
, d.h., für alle reellen Zahlen x gilt:
.
Der Graph einer ungeraden Funktion ist
zum
.

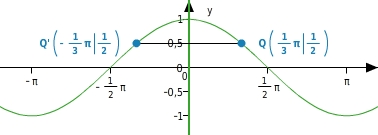
Die Kosinusfunktion ist eine
, d.h., für alle reellen Zahlen x gilt:
.
Der Graph einer geraden Funktion ist
zur y-Achse.

Trigonometrische Gleichungen lösen
Um trigonometrische Gleichungen wie z.B.
oder
zu lösen, kannst du die Symmetrien und die Periodizität der Winkelfunktionen nutzen.
Denn, wenn du die Lösungen einer Gleichung im Intervall - π ; π kennst, kennst du alle Lösungen für den gesamten Definitionsbereich.
Lösungen im Intervall - π ; π :
;
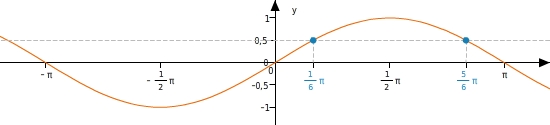 Die Periode ist
, also findest du alle anderen Lösungen, indem du auf die bereits gefundenen Lösungen ganzzahlige Vielfache von
addierst.
Da du nicht alle Lösungen einzeln aufschreiben kannst, fasst du sie in der
zusammen:
Die Periode ist
, also findest du alle anderen Lösungen, indem du auf die bereits gefundenen Lösungen ganzzahlige Vielfache von
addierst.
Da du nicht alle Lösungen einzeln aufschreiben kannst, fasst du sie in der
zusammen:
 Die Periode ist
, also findest du alle anderen Lösungen, indem du auf die bereits gefundenen Lösungen ganzzahlige Vielfache von
addierst.
Da du nicht alle Lösungen einzeln aufschreiben kannst, fasst du sie in der
zusammen:
Die Periode ist
, also findest du alle anderen Lösungen, indem du auf die bereits gefundenen Lösungen ganzzahlige Vielfache von
addierst.
Da du nicht alle Lösungen einzeln aufschreiben kannst, fasst du sie in der
zusammen:
Lies:
ist die Menge aller
aus ℝ mit
oder
und
aus ℤ.
Lösungen im Intervall - π ; π :
;
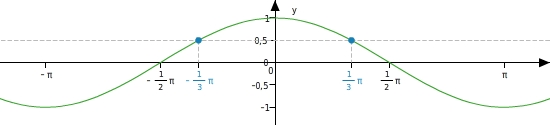

Wegen der
des Graphen (der Kosinus ist eine gerade Funktion) gilt für alle x im Intervall - π ; π :
.

