Daten, Diagramme und Häufigkeiten
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenLerninhalte
- Säulen- und Kurvendiagramme interaktiv selbst erstellen
- Interpretieren von Säulen-, Kreis-, Balken-, Streifen- und Kurvendiagrammen
- Anwendungsaufgaben zu den Begriffen Mittelwert und Median
- Absolute und relative Häufigkeiten in Sachsituationen unterscheiden und ermitteln lernen
- Zufallsexperimente (z.B. Glücksrad drehen, Würfeln) und deren Ausgang kennenlernen und beurteilen
- Wahrscheinlichkeiten von einfachen Zufallsexperimenten bestimmen
Diagramme erstellen und interpretieren
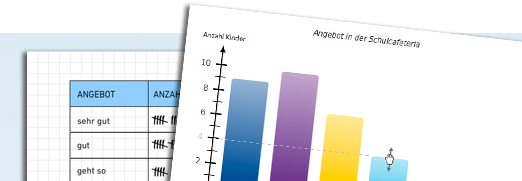Selbst machen ist der beste Weg um neue Darstellungsarten kennen und verstehen zu lernen. Die zur Erstellung eines Diagramms notwendigen Werte sind in der Aufgabenstellung vorgegeben und sollen übertragen werden. Die einzelnen Wertebalken werden mit der Maus bis zu jener Stelle gezogen, die dem jeweiligen Wert in der Vorgabe entspricht. Finde den Unterschied
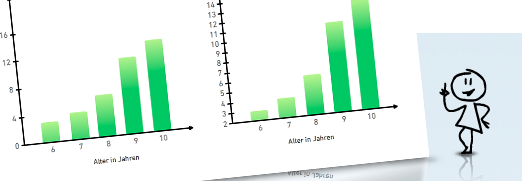Bettermarks überprüft die Fähigkeit zur Interpretation von Diagrammen. Durch einfache Manipulation an der Achsenbeschriftung erscheint der gleiche Sachverhalt plötzlich anders. Aber mit dem neu erlangten Wissen über Diagramme und einem prüfenden Auge geht man solchen Aufgaben nicht auf den Leim. Oder" Ein Baum ohne Blätter
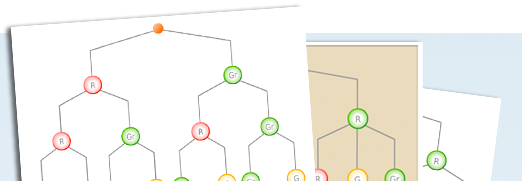Baumdiagramme helfen, komplexe Sachverhalte analytisch zu betrachten. Aus drei vorgegebenen Antworten muss die richtige herausgesucht werden. Die Lösung der Aufgabe erfordert genaues Lesen der Fragestellung. Denn diese gibt einen Anhaltspunkt, welche der vorgegebenen Antworten zur Frage gehört. Alles Zufall oder was?
Relative und absolute Häufigkeiten müssen intuitiv auf Spielsituationen angewendet werden um die Frage nach der besten Gewinnchance zu beantworten.