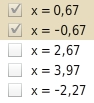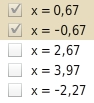Bruchgleichungen lösen und darstellen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, wie du Bruchgleichungen durch Probieren, graphisch oder durch Umformungen lösen kannst.Eine Bruchgleichung ist eine Gleichung die Bruchterme enthält.
Da Bruchgleichungen nicht für alle Zahlen definiert sein müssen, bestimmst du den maximalen Definitionsbereich aller Bruchterme und versicherst dich, dass jeder berechnete Wert für die unbekannte Variable im Definitionsbereich jedes Bruchterms enthalten ist.
Lösen durch Probieren
Einfache Bruchgleichungen kannst du durch Probieren lösen.Wenn du einen Wert für die Variable
gewählt hast, überprüfst du, ob die Bruchterme auf beiden Seiten denselben Wert für
ergeben.Außerdem überprüfst du, ob die Bruchterme für den gefundenen Wert
definiert sind.
Welche der Zahlen 5;
und
ist eine Lösung der Bruchgleichung
?
Werte einsetzen und berechnen
Du setzt die Werte für
in die Bruchterme
und
ein und prüfst, ob die Termwerte gleich sind.Hier ergibt nur
eine wahre Aussage.Du setzt
in den Term
ein:
 Du setzt
in den Term
ein:
Du setzt
in den Term
ein:
 Die Ergebnisse sind gleich und die Bruchterme
und
sind für
definiert.
ist eine Lösung der Bruchgleichung.
Die Ergebnisse sind gleich und die Bruchterme
und
sind für
definiert.
ist eine Lösung der Bruchgleichung.
 Du setzt
in den Term
ein:
Du setzt
in den Term
ein:
 Die Ergebnisse sind gleich und die Bruchterme
und
sind für
definiert.
ist eine Lösung der Bruchgleichung.
Die Ergebnisse sind gleich und die Bruchterme
und
sind für
definiert.
ist eine Lösung der Bruchgleichung.
ist Lösung der Bruchgleichung
.
Ist die Zahl 1 eine Lösung der Bruchgleichung
?
Termwerte berechnen
Du setzt 1 für
in beide Bruchterme ein und überprüfst, ob die Ergebnisse gleich sind.Linke Seite:
Rechte Seite:
Die beiden Werte sind verschieden, also ist 1 keine Lösung der Bruchgleichung.
Nein, 1 ist keine Lösung der Bruchgleichung.
Ist 2 oder 3 eine Lösung der Gleichung
?
Termwert berechnen
Die Bruchterme sind für
nicht definiert, da in beiden Fällen der Nenner null wird.Also kann 3 keine Lösung der Bruchgleichung sein.
Beide Bruchterme sind für
definiert.
Du setzt 2 für
in beide Bruchterme ein und überprüfst, ob die Termwerte gleich sind.
Linke Seite:
Rechte Seite:
=-6
Die beiden Werte stimmen überein, also ist 2 eine Lösung der Bruchgleichung.
Bruchgleichungen können auch mehrere Lösungen haben.Bei diesem Beispiel ist 1 eine weitere Lösung.
2 ist Lösung der Bruchgleichung
Graphisch lösen
An der Stelle, an der sich zwei Funktionsgraphen schneiden, haben die Funktionsterme denselben Wert. Du betrachtest die Bruchterme beider Seiten einer Bruchgleichung also als Funktionsterme zweier gebrochen-rationaler Funktionen und stellst die zugehörigen Graphen in einem Koordinatensystem dar. Die
-Koordinate des Schnittpunktes beider Graphen ist die Lösung der Bruchgleichung.
Gegeben sind die Graphen zu den Funktionstermen
und
.
Lies die Lösung der Gleichung
im Koordinatensystem ab.
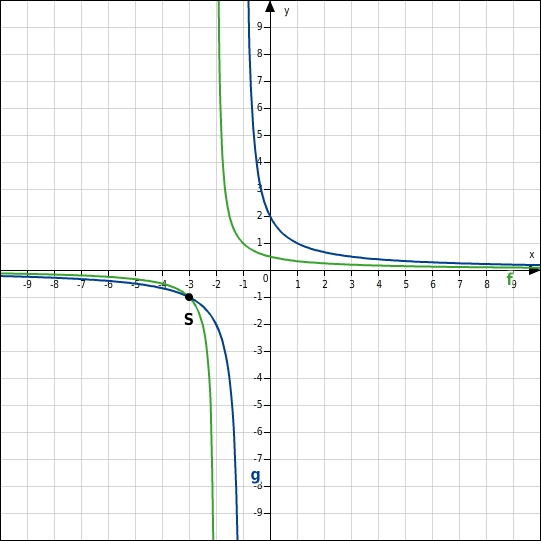

-Koordinate ablesen
Der Schnittpunkt hat die Koordinaten -3 | - 1 , die Lösung der Bruchgleichung ist also
.
Lösen durch Umformen
Um eine Bruchgleichung zu lösen, kannst du die Gleichung in eine nennerfreie Gleichung umformen.
Beachte, dass die Bruchgleichung und die umgeformte Gleichung verschiedene Definitionsbereiche haben können.Du bestimmst also zuerst den maximalen Definitionsbereich der Bruchterme.
Enthält die Bruchgleichung nur einen Bruchterm, dann multiplizierst du die gesamte Gleichung mit dem Nenner dieses Bruchterms.
Bestimme den maximalen Definitionsbereich
der Bruchgleichung
in der Grundmenge ℚ und löse sie.
Definitionsbereich bestimmen
Der Bruchterm
ist für
nicht definiert, denn
für
.
Lösungsmenge bestimmen
Du multiplizierst beide Seiten der Gleichung mit dem Nenner
und erhältst eine nennerfreie Gleichung:
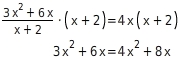 Diese Gleichung löst du nach
auf:
Diese Gleichung löst du nach
auf:
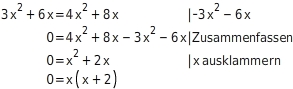 Also:
und
Da -2 aber nicht im Definitionsbereich enthalten ist, ist -2 keine Lösung der Bruchgleichung.
Also:
und
Da -2 aber nicht im Definitionsbereich enthalten ist, ist -2 keine Lösung der Bruchgleichung.
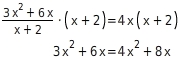 Diese Gleichung löst du nach
auf:
Diese Gleichung löst du nach
auf:
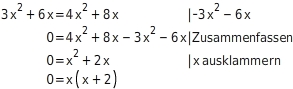 Also:
und
Da -2 aber nicht im Definitionsbereich enthalten ist, ist -2 keine Lösung der Bruchgleichung.
Also:
und
Da -2 aber nicht im Definitionsbereich enthalten ist, ist -2 keine Lösung der Bruchgleichung.
Lösen durch Multiplizieren mit dem HauptnennerEnthält die Bruchgleichung mehrere Bruchterme, dann multiplizierst du beide Seiten der Bruchgleichung mit dem Hauptnenner.
Bestimme den maximalen Definitionsbereich
der Bruchgleichung
in der Grundmenge ℚ und löse sie.
Definitionsbereich bestimmen
Beide Bruchterme sind für
nicht definiert, denn
für
.Der Bruchterm
ist außerdem auch für
nicht definiert, denn der Nenner enthält
als Faktor.
Gleichung lösen
Der Hauptnenner der Bruchterme ist
.
Du multiplizierst beide Seiten der Gleichung mit dem Hauptnenner und erhältst eine nennerfreie Gleichung:
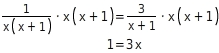 Diese Gleichung löst du nach
auf.
Diese Gleichung löst du nach
auf.
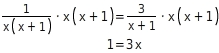 Diese Gleichung löst du nach
auf.
Diese Gleichung löst du nach
auf.
Lösen durch Multiplizieren über KreuzEnthält die Bruchgleichung auf jeder Seite nur einen Bruchterm, so multiplizierst du über Kreuz.
Löse die Bruchgleichung
.
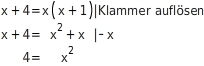 gilt nur für
und für
Die Bruchterme sind für
und für
definiert.
gilt nur für
und für
Die Bruchterme sind für
und für
definiert.
über Kreuz multiplizieren
Du multiplizierst den Zähler der linken Seite mit dem Nenner der rechten Seite und den Zähler der rechten Seiten mit dem Nenner der linken Seite:
 Vergiss die Klammern nicht.
Vergiss die Klammern nicht.
Lösungsmenge bestimmen
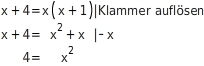 gilt nur für
und für
Die Bruchterme sind für
und für
definiert.
gilt nur für
und für
Die Bruchterme sind für
und für
definiert.
Gleichungen mit Potenzrechnung lösen
In speziellen Fällen kannst du Bruchgleichungen auch mit Hilfe der Potenzrechenregeln lösen. Du formst die Gleichung so um, dass eine Gleichung der Form
oder der Form
entsteht, von der du weißt, dass
eine Quadratzahl und
ein Kubikzahl ist.Sind
und
keine zweiten oder dritten Potenzen von ganzen Zahlen, so löst du die Gleichung näherungsweise mit Hilfe eines Funktionsgraphen.
Gib alle Lösungen der Gleichung
an.
Lösungen angeben
Du schreibst die Bruchterme, die beide auf ℚ ∖ {0 } definiert sind, als Potenzen mit negativen Exponenten und wendest die Rechenregeln der Potenzrechnung an:
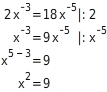 Also
und
.
Also
und
.
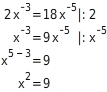 Also
und
.
Also
und
.
L = {
;
}
Gib alle Lösungen der Gleichung
an.
Lösungen angeben
Du schreibst die Bruchterme, die beide auf ℚ ∖ {0 } definiert sind, als Potenzen mit negativen Exponenten und wendest die Rechenregeln der Potenzrechnung an:
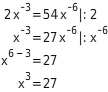 Also
.
Also
.
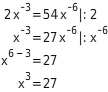 Also
.
Also
.
L = {
}
Gib alle Lösungen der Gleichung
an. Schaue dir dazu den Graphen der Funktion f mit
an:
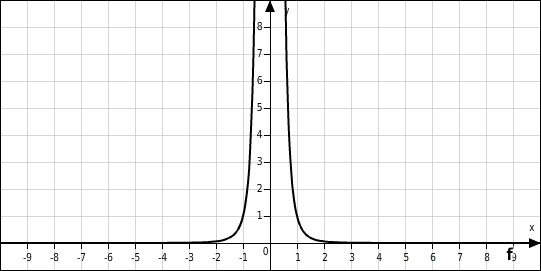

Lösungen angeben
Du suchst die Schnittpunkte des Graphen mit der Geraden
und liest die
-Koordinaten an der
-Achse ab.
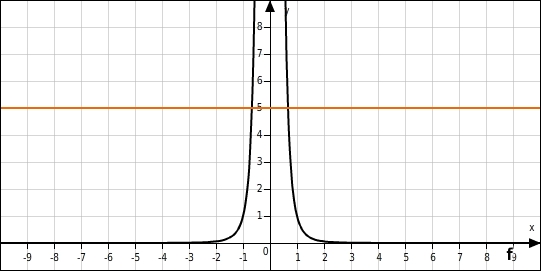

Gerundete Lösungen der Gleichung: