Anwendungen zum Satz des Pythagoras
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du den Satz des Pythagoras auf mathematische Probleme aus dem Alltag anwenden kannst.
Lösen von Anwendungsaufgaben Schritt für Schritt
Der Satz des Pythagoras hat eine Vielzahl von Anwendungen: mit Hilfe des Satzes lassen sich zum Beispiel die Bildschirmdiagonale eines Fernsehers, die Höhe einer Leiter, Entfernungen in Luftlinie und vieles mehr berechnen. In diesen Anwendungen ist immer rechtwinkliges Dreieck im Spiel, doch dies ist nicht immer so offensichtlich. Deshalb ist es wichtig, dass du beim Lösen solcher Aufgaben Schritt für Schritt vorgehst.


Üblicherweise gibt man bei einem Bildschirm die Länge der Diagonalen in Zoll (1" =
2.54cm) an. Berechne dieses Maß für das abgebildete Modell. Gib die Länge der Diagonalen (in Zoll) auf halbe Zoll genau an.
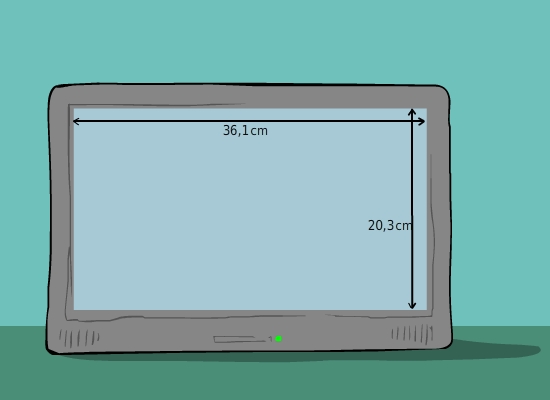

Diagonale berechnen
Um die Länge d der Diagonalen zu berechnen, betrachtest du das rechtwinklige Dreieck.
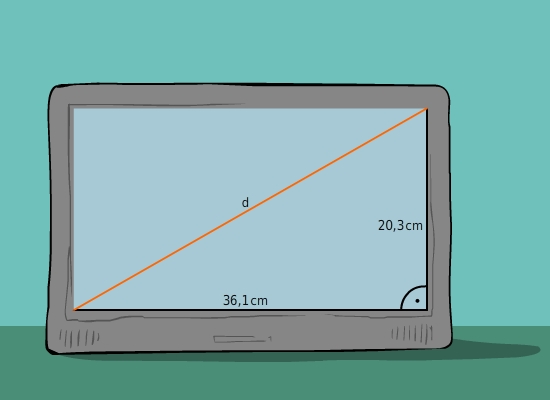 Die Diagonale
ddes Bildschirms ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite und die Höhe des Bildschirms sind die beiden Katheten. Gegeben sind die Längen der beiden Katheten (Breite
36.1cmund Höhe
20.3cmdes Bildschirms), gesucht ist die Länge der Hypotenuse (Länge der Bildschirmdiagonalen d). Die Diagonale in Zentimetern berechnest du mit Hilfe des Satzes des Pythagoras:
Die Diagonale
ddes Bildschirms ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite und die Höhe des Bildschirms sind die beiden Katheten. Gegeben sind die Längen der beiden Katheten (Breite
36.1cmund Höhe
20.3cmdes Bildschirms), gesucht ist die Länge der Hypotenuse (Länge der Bildschirmdiagonalen d). Die Diagonale in Zentimetern berechnest du mit Hilfe des Satzes des Pythagoras:
 Du ziehst die Wurzel:
d≈
41.4
Du rechnest in Zoll um und rundest:
41.4 : 2.54≈
16.299...
Also:
d≈
16.3
Du ziehst die Wurzel:
d≈
41.4
Du rechnest in Zoll um und rundest:
41.4 : 2.54≈
16.299...
Also:
d≈
16.3
 Die Diagonale
ddes Bildschirms ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite und die Höhe des Bildschirms sind die beiden Katheten. Gegeben sind die Längen der beiden Katheten (Breite
36.1cmund Höhe
20.3cmdes Bildschirms), gesucht ist die Länge der Hypotenuse (Länge der Bildschirmdiagonalen d). Die Diagonale in Zentimetern berechnest du mit Hilfe des Satzes des Pythagoras:
Die Diagonale
ddes Bildschirms ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite und die Höhe des Bildschirms sind die beiden Katheten. Gegeben sind die Längen der beiden Katheten (Breite
36.1cmund Höhe
20.3cmdes Bildschirms), gesucht ist die Länge der Hypotenuse (Länge der Bildschirmdiagonalen d). Die Diagonale in Zentimetern berechnest du mit Hilfe des Satzes des Pythagoras:
Die Diagonale ist
16.3Zoll lang.
Wie hoch reicht die Leiter?
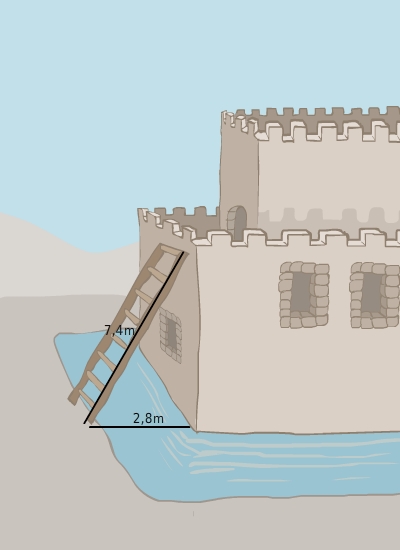

Höhe berechnen
Um die Höhe h der Leiter zu berechnen, betrachtest du das rechtwinklige Dreieck.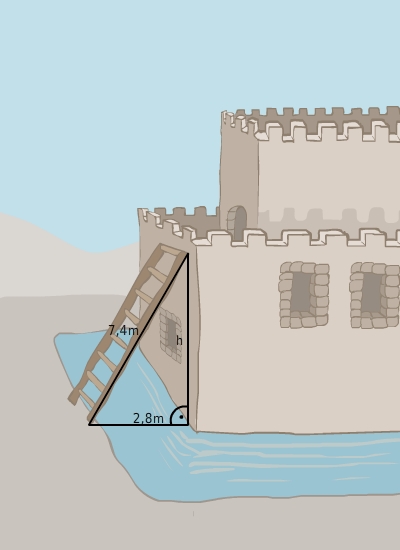 Die Leiter ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite des Wassergrabens und die Höhe der Leiter sind die beiden Katheten. Gegeben sind die Länge der Hypotenuse (Länge der Leiter
7.4 m) und die Länge einer Kathete (Breite des Wassergrabens
2.8 m). Gesucht ist die Länge
hder anderen Kathete (Leiterhöhe in
m).Nach dem Satz des Pythagoras gilt:
Die Leiter ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite des Wassergrabens und die Höhe der Leiter sind die beiden Katheten. Gegeben sind die Länge der Hypotenuse (Länge der Leiter
7.4 m) und die Länge einer Kathete (Breite des Wassergrabens
2.8 m). Gesucht ist die Länge
hder anderen Kathete (Leiterhöhe in
m).Nach dem Satz des Pythagoras gilt: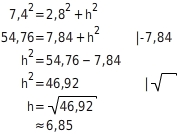
 Die Leiter ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite des Wassergrabens und die Höhe der Leiter sind die beiden Katheten. Gegeben sind die Länge der Hypotenuse (Länge der Leiter
7.4 m) und die Länge einer Kathete (Breite des Wassergrabens
2.8 m). Gesucht ist die Länge
hder anderen Kathete (Leiterhöhe in
m).Nach dem Satz des Pythagoras gilt:
Die Leiter ist die Hypotenuse des rechtwinkligen Dreiecks, die Breite des Wassergrabens und die Höhe der Leiter sind die beiden Katheten. Gegeben sind die Länge der Hypotenuse (Länge der Leiter
7.4 m) und die Länge einer Kathete (Breite des Wassergrabens
2.8 m). Gesucht ist die Länge
hder anderen Kathete (Leiterhöhe in
m).Nach dem Satz des Pythagoras gilt: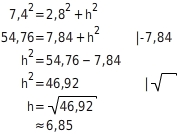
Die Höhe beträgt
6.85 m.
Um den Baum zu fällen, befestigt der Holzfäller ein Seil an der Spitze des Baumes und zieht daran. Wie lang muss das Seil mindestens sein, damit der Holzfäller den Baum nicht auf den Kopf bekommt?


Länge berechnen
Um einen Unfall zu vermeiden, muss der Holzfäller außer Reichweite des kippenden Baumes stehen. Diese ist gleich der Höhe des Baumes von der Kerbe bis zur Spitze:
12m-1m=11mUm zu überprüfen, ob der Holzfäller in sicherem Abstand d zum fallenden Baum steht, betrachtest du das rechtwinklige Dreieck.
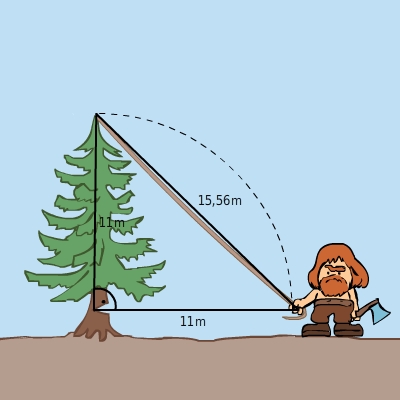 Das gespannte Seil ist die Hypotenuse, der Baum (ohne Stumpf) ist eine Kathete und die Entfernung zwischen dem Baum und dem Holzfäller ist die andere Kathete.Gegeben sind die Längen der Katheten (beide gleich
11 m).Gesucht ist die Länge
xder Hypotenuse (Seillänge in
m).
Du stellst die Gleichung für den Satz des Pythagoras auf und löst diese nach x auf:
Das gespannte Seil ist die Hypotenuse, der Baum (ohne Stumpf) ist eine Kathete und die Entfernung zwischen dem Baum und dem Holzfäller ist die andere Kathete.Gegeben sind die Längen der Katheten (beide gleich
11 m).Gesucht ist die Länge
xder Hypotenuse (Seillänge in
m).
Du stellst die Gleichung für den Satz des Pythagoras auf und löst diese nach x auf: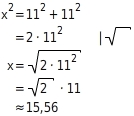
 Das gespannte Seil ist die Hypotenuse, der Baum (ohne Stumpf) ist eine Kathete und die Entfernung zwischen dem Baum und dem Holzfäller ist die andere Kathete.Gegeben sind die Längen der Katheten (beide gleich
11 m).Gesucht ist die Länge
xder Hypotenuse (Seillänge in
m).
Du stellst die Gleichung für den Satz des Pythagoras auf und löst diese nach x auf:
Das gespannte Seil ist die Hypotenuse, der Baum (ohne Stumpf) ist eine Kathete und die Entfernung zwischen dem Baum und dem Holzfäller ist die andere Kathete.Gegeben sind die Längen der Katheten (beide gleich
11 m).Gesucht ist die Länge
xder Hypotenuse (Seillänge in
m).
Du stellst die Gleichung für den Satz des Pythagoras auf und löst diese nach x auf: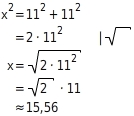
Das Seil muss mindestens
15.56 mlang sein.
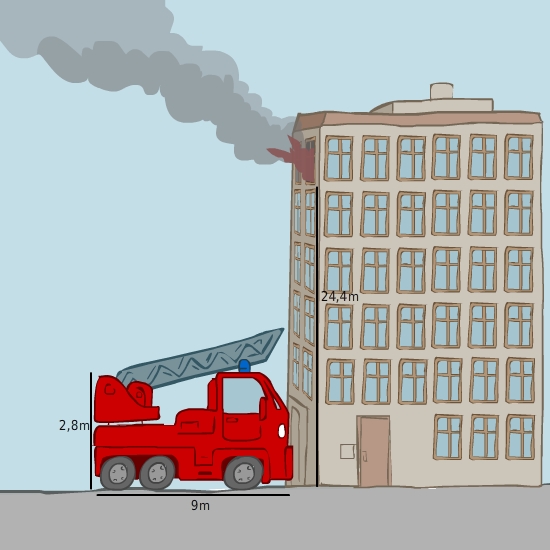
Die Leiter des Feuerwehrfahrzeugs kann bis zu einer Länge von
22 mausgefahren werden. Reicht die Leiter bis zum Fenster?

Höhe berechnen
Um die Gesamthöhe h der Leiter zu berechnen, betrachtest du das rechtwinklige Dreieck.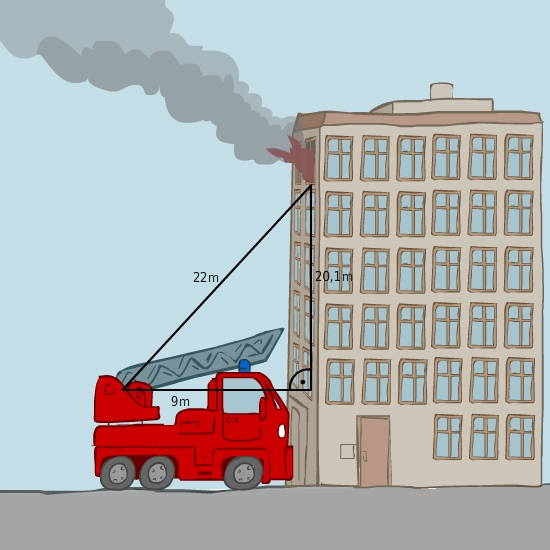 Die Leiter ist die Hypotenuse, das Fahrzeug bildet die eine Kathete und die Strecke an der Hauswand, soweit die Leiter vom Fahrzeug aus reicht, die andere Kathete.Gegeben sind die Länge der Hypotenuse (Leiterlänge
22 m) und die Länge der einen Kathete (Fahrzeuglänge
9 m). Gesucht ist die Länge
ader anderen Kathete (Reichweite in
m). Die Gesamthöhe der Leiter berechnest du zum Schluss, indem du zu
adie Fahrzeughöhe
2.8 maddierst. Nach dem Satz des Pythagoras gilt:
Die Leiter ist die Hypotenuse, das Fahrzeug bildet die eine Kathete und die Strecke an der Hauswand, soweit die Leiter vom Fahrzeug aus reicht, die andere Kathete.Gegeben sind die Länge der Hypotenuse (Leiterlänge
22 m) und die Länge der einen Kathete (Fahrzeuglänge
9 m). Gesucht ist die Länge
ader anderen Kathete (Reichweite in
m). Die Gesamthöhe der Leiter berechnest du zum Schluss, indem du zu
adie Fahrzeughöhe
2.8 maddierst. Nach dem Satz des Pythagoras gilt: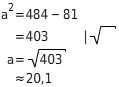 Die Leiter reicht also maximal
(20.1+2.8)m=22.9mhoch und erreicht daher das Fenster nicht.
Die Leiter reicht also maximal
(20.1+2.8)m=22.9mhoch und erreicht daher das Fenster nicht.
 Die Leiter ist die Hypotenuse, das Fahrzeug bildet die eine Kathete und die Strecke an der Hauswand, soweit die Leiter vom Fahrzeug aus reicht, die andere Kathete.Gegeben sind die Länge der Hypotenuse (Leiterlänge
22 m) und die Länge der einen Kathete (Fahrzeuglänge
9 m). Gesucht ist die Länge
ader anderen Kathete (Reichweite in
m). Die Gesamthöhe der Leiter berechnest du zum Schluss, indem du zu
adie Fahrzeughöhe
2.8 maddierst. Nach dem Satz des Pythagoras gilt:
Die Leiter ist die Hypotenuse, das Fahrzeug bildet die eine Kathete und die Strecke an der Hauswand, soweit die Leiter vom Fahrzeug aus reicht, die andere Kathete.Gegeben sind die Länge der Hypotenuse (Leiterlänge
22 m) und die Länge der einen Kathete (Fahrzeuglänge
9 m). Gesucht ist die Länge
ader anderen Kathete (Reichweite in
m). Die Gesamthöhe der Leiter berechnest du zum Schluss, indem du zu
adie Fahrzeughöhe
2.8 maddierst. Nach dem Satz des Pythagoras gilt: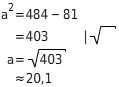 Die Leiter reicht also maximal
(20.1+2.8)m=22.9mhoch und erreicht daher das Fenster nicht.
Die Leiter reicht also maximal
(20.1+2.8)m=22.9mhoch und erreicht daher das Fenster nicht.
Die Leiter reicht maximal
22.9 mhoch und reicht daher nicht bis zum Fenster.
Rechtwinkligkeit prüfen
Mit Hilfe des Satzes des Pythagoras und seiner Umkehrung kannst du prüfen, ob ein Winkel rechtwinklig ist, indem du diese Schritte befolgst :


Mit Hilfe eines Maßbandes möchte Lukas prüfen, ob die Ecke seines Klassenzimmers wirklich rechtwinklig sind.
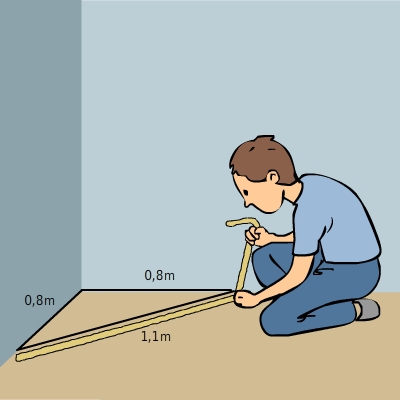

Rechtwinkligkeit prüfen
Ein Dreieck mit den Seiten a, b und c ist rechtwinklig mit der Hypotenuse c, wenn
a2+b2=c2gilt. Du berechnest beide Seiten der Formel mit den Werten
0.8für a,
0.8für b und
1.1für c.
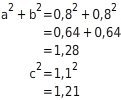 Die Gleichung
a2+b2=c2ist nicht erfüllt, also ist die Ecke kein rechter Winkel.
Die Gleichung
a2+b2=c2ist nicht erfüllt, also ist die Ecke kein rechter Winkel.
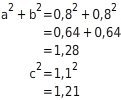 Die Gleichung
a2+b2=c2ist nicht erfüllt, also ist die Ecke kein rechter Winkel.
Die Gleichung
a2+b2=c2ist nicht erfüllt, also ist die Ecke kein rechter Winkel.
Die Ecke ist nicht rechtwinklig.

