Anwendungen zum Lösen von Exponentialgleichungen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenLösen von Anwendungsaufgaben Schritt für Schritt
Wird zu einem Wachstumsprozess danach gefragt, nach wie vielen Schritten (nach welcher Zeit) ein bestimmter Wert oder Anteil erreicht wird, kannst du die gesuchte Größe ermitteln, indem du eine Exponentialgleichung der Form
aufstellst und diese löst. Dabei gehst du Schritt für Schritt vor:
Ermittle aus dem Text den
, den Anfangswert
und den gewünschten Zielwert (Funktionswert an der gesuchten Stelle
).
Durch
oder Exponentenvergleich kannst du die Exponentialgleichung in eine
oder
umwandeln.
Du löst die lineare Gleichung mit Hilfe von
oder die quadratische Gleichung mit Hilfe der
(
).
Du überprüfst, ob die Lösung auch eine Lösung für die konkrete Fragestellung ist.
Ermittle aus dem Text den
, den Anfangswert
und den gewünschten Zielwert (Funktionswert an der gesuchten Stelle
).
Durch
oder Exponentenvergleich kannst du die Exponentialgleichung in eine
oder
umwandeln.
Du löst die lineare Gleichung mit Hilfe von
oder die quadratische Gleichung mit Hilfe der
(
).
Du überprüfst, ob die Lösung auch eine Lösung für die konkrete Fragestellung ist.
Am Ufer eines Sees wurden vor 2 Wochen Seerosen angepflanzt. Sie haben bereits etwa
der Wasseroberfläche bedeckt. Die bedeckte Fläche verdoppelt sich jede Woche.
Der See ist nach etwa 10 Wochen vollständig bedeckt.
Die Lösung ist durchaus plausibel, denn
Die Lösung ist durchaus plausibel, denn
Logarithmische Einteilung
Um die Werte exponentiell wachsender Funktionen übersichtlich darstellen zu können, wird oft eine logarithmische Einteilung an den Koordinatenachsen gewählt. Der Graph der Funktion wird dann eine Gerade.
Die
zur Angabe von Erdbebenstärken
Der Unterschied von einem Punkt auf der Richterskala entspricht einem etwa zehnfach höheren Ausschlag (Amplitude) im Seismogramm und einer etwa 32-fachen Energiefreisetzung im Erdbebenherd.
Ein Erdbeben der Stärke 1 bis 3 wird als Mikrobeben bezeichnet. Es wird vom Menschen nicht wahrgenommen und wird nur von in der unmittelbaren Nähe befindlichen Seismographen erfasst.
Beben mit einer Stärke von etwa
und höher werden von Seismographen auf der ganzen Welt erfasst.
Aber erst ab einer Stärke von mehr als 5 spricht man von einem mäßigen Erdbeben.
Auch die in Dezibel gemessene Lautstärke wird an einer logarithmischen Skala dargestellt.
Bei einer Zunahme von 20 Dezibel erhöht sich die Intensität der Lautstärke (physikalische Lautstärke = Schalldruck) auf das 10-fache.
Die Dezibelskala
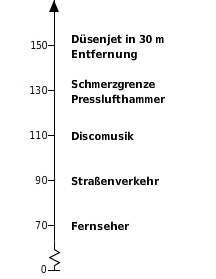
Die vom menschlichen Ohr empfundene physiologische Lautstärke wächst langsamer als die physikalische Lautstärke. Ein Unterschied von 10 dB wird schon als Verdopplung oder Halbierung der Laustärke empfunden.
