Antiproportionale Zuordnungen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, was antiproportionale Zuordnungen sind und wie du sie erkennen, konstruieren und graphisch darstellen kannst.
Antiproportionale Zuordnungen und ihre Wertetabellen
Zuordnungen werden als antiproportional bezeichnet, wenn das Produkt einander zugeordneter Werte immer gleich ist.Das Produkt nennt man dann Antiproportionalitätsfaktor.
Für eine antiproportionale Zuordnung gilt die Aussage „je mehr, desto weniger“.Wenn diese verletzt ist, ist die Zuordnung nicht antiproportional.Wenn sie gilt, ist sie möglicherweise antiproportional.
Der Antiproportionalitätsfaktor ist immer das Produkt von zwei Werten aus einer Spalte.
Die untere Zeile berechnest du aus der oberen durch Division des Antiproportionalitätsfaktors.
Zuordnungen an Wertetabellen
Kosten in Höhe von
werden von einer Person alleine oder mehreren zusammen bezahlt.Den Teilnehmerzahlen 1, 3 und 4 sollen antiproportional die entsprechenden Kosten pro Person in Euro zugeordnet werden.
Erstelle die Wertetabelle für diese Zuordnung.
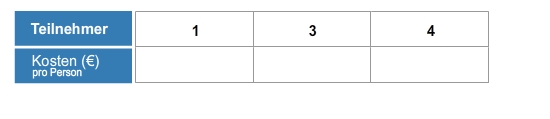
Wertetabelle erstellen
Der Antiproportionalitätsfaktor ist hier
.
Wie zu erkennen ist, wird bei einer antiproportionalen Zuordnung die 1 immer dem Antiproportionalitätsfaktor zugeordnet.
Ist diese Zuordnung antiproportional?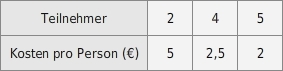
Antiproportionale Zuordnung erkennen
Zur überprüfung der Antiproportionalität löst du diese drei Multiplikationsaufgaben:
Die Lösung ist in allen drei Fällen gleich. Die Zuordnung ist daher antiproportional mit dem Antiproportionalitätsfaktor
.
Ist diese Zuordnung antiproportional?
Eigenschaft bestimmen
Zur überprüfung der Antiproportionalität löst du diese drei Multiplikationsaufgaben:
Bei antiproportionalen Zuordnungen ist das Produkt von Ausgangswert und zugeordnetem Wert immer gleich. Hier sind die Lösungen nicht identisch, also ist diese Zuordnung nicht antiproportional.
Zuordnungen im Alltag
Ein Geldgewinn soll gerecht unter allen Gewinnern aufgeteilt werden. Die Anzahl der Gewinner wird dem jeweiligen Gewinn pro Person zugeordnet.
Anzahl der Gewinner 
Gewinn pro Person
Ist diese Zuordnung antiproportional?
Gewinn pro Person
Ist diese Zuordnung antiproportional?
Eigenschaft bestimmen
Je mehr Gewinner es gibt, umso weniger Geld bekommt ein einzelner.Dabei steht die Höhe des Gesamtgewinns, der aufgeteilt wird, fest. Sie ist der Antiproportionalitätsfaktor.Diese Zuordnung ist antiproportional
Graphen antiproportionaler Zuordnungen
Zuordnungen von Zahlen können in einem Koordinatensystem dargestellt werden. Jedes Zahlenpaar entspricht einem Punkt im Koordinatensystem.
Wenn du eine antiproportionale Zuordnung graphisch darstellst, liegen die Punkte immer zusammen auf einer Hyperbel.Diese Hyperbel verläuft oben links nach unten rechts stets fallend, da die Aussage „je mehr, desto weniger“ gilt.
Graphen zeichnen
Trage die Werte dieser antiproportionalen Zuordnung in das Koordinatensystem ein!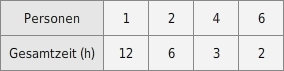
Markieren von Punkten im Koordinatensystem
Um die antiproportionale Zuordnung aus dieser Wertetabellezu skizzieren, markierst du die vier Punkte (1|12), (2|6), (4|3) und (6|2) im Koordinatensystem.Die Achsen werden meist wie die Tabellen in der ersten Spalte beschriftet.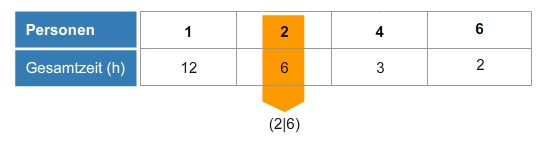
Wie bei jeder antiproportionalen Zuordnung liegen die Punkte auf einer gemeinsamen Hyperbel.
Wie bei jeder antiproportionalen Zuordnung liegen die Punkte auf einer gemeinsamen Hyperbel.Graphen erkennen
Welcher Graph stellt eine antiproportionale Zuordnung dar?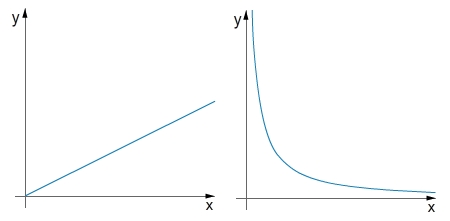
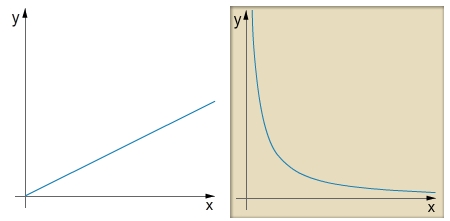
Graph auswählen
Eine durchgängige antiproportionale Zuordnung entspricht immer einer Hyperbel.
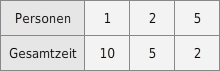
Welcher Graph gehört zu dieser antiproportionalen Zuordnung?
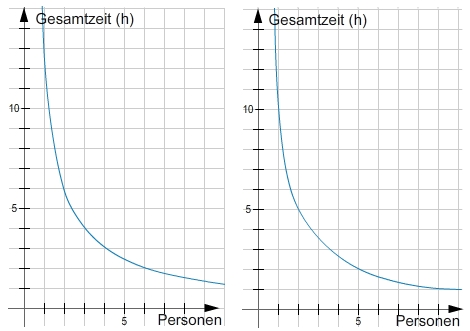
Zugehörigen Graph erkennen
Beide Graphen stellen antiproportionale Zuordnungen dar.Du musst also die Punkte für ein Wertepaar in beiden Graphen genau ablesen.Hier liegt der Punkt (2|5) aus der zweiten Tabellenspalte nur auf der Hyperbel rechts im Bild.
Antiproportionales Rechnen
Ist bei einer antiproportionalen Zuordnung ein Wertepaar gegeben, so kannst du den Zuordnungswert jeder weiteren Zahl berechnen.
Bei den Rechnungen hilft dir die Dreisatztabelle. In den folgenden Beispielen wird dir gezeigt, wie du diese Tabelle benutzen kannst.
Führe beim antiproportionalen Rechnen in der zweiten Spalte der Tabelle immer die jeweils umgekehrte Punktrechnung aus.
Antiproportionale Zuordnung mit Eins als übergangswert
Berechne, wie lange 5 Personen für eine Arbeit brauchen, die 2 Personen in 12 Stunden erledigen können.
Antiproportionale Zuordnung
Antiproportionale Zuordnung mit größtem gemeinsamen Teiler als übergangswert
Manchmal sind die gegebenen Zahlen so beschaffen, dass es umständlich ist, mit dem übergangswert 1 zu rechnen. Dann kannst du den größten gemeinsamen Teiler nutzen.
Gegeben ist eine antiproportionale Zuordnung.Berechne den gesuchten Preis bei 15 Personen, indem du die Tabelle dieser Zuordnung vollständig ausfüllst.
Antiproportionale Zuordnung
Bei 9 Personen beträgt der Preis
. Du suchst den Preis bei 15 Personen.
Dazu rechnest du zunächst von 9 Personen auf eine Person zurück. Du dividierst also links durch 9. Da die Zuordnung antiproportional ist machst du rechts genau das Umgekehrte: Du multiplizierst mit 9.
Damit du den Preis bei 15 Personen erhältst, multiplizierst du nun links mit 15 und machst rechts gleichzeitig wieder die Umkehrung.
Antiproportionale Zuordnung in einer Textaufgabe
Familie Meier plant einen Urlaub in einem Ferienhaus.Zu viert würden sie
pro Person bezahlen. Nun planen sie aber mit sechs Personen dort zu wohnen und überlegen, wie teuer es pro Person wird.
Entscheide, ob die betrachtete Zuordnung antiproportional ist und berechne anschließend das Ergebnis.
Antiproportionale Zuordnung erkennen
Bei der Berechnung von Kosten pro Person bei festen Gesamtkosten werden diese gleichmäßig aufgeteilt.Je mehr Personen teilnehmen, umso geringer werden die Kosten pro Person.
Daher ist die ZuordnungAnzahl der Personen 
Kosten pro Personin diesen Fällen immer antiproportional.
Kosten pro Personin diesen Fällen immer antiproportional.
Antiproportionale Zuordnung
Wenn du in der linken Spalte dividierst, musst du in der rechten Spalte mit der gleichen Zahl multiplizieren und umgekehrt.
Für vier Personen kostet das Haus
pro Person, also ist es für jede von zwei Personen doppelt so teuer:
.Sechs Personen sind dreimal so viele wie zwei, also kostet es dann pro Person ein Drittel von
.
Antwortsatz vervollständigen
Du liest das Ergebnis in der letzten Zeile der Tabelle ab.Wenn sechs Personen mitfahren, entstehen für das Haus
Kosten pro Person.
Bei sechs Urlaubern kostet das Haus pro Person
€.
