Analysis
Unter Analysis versteht man das Studium reeller Funktionen mit Hilfe der Differenzial- und Integralrechnung. Die Grundlagen hierzu wurden um 1670 von Isaak Newton und Gottfried Wilhelm Leibniz geschaffen. Die Analysis hat sich seither weit verzweigt. Sie wurde auf Funktionen komplexer Variablen (Funktionentheorie) und auf Funktionen, deren Argumente selbst wieder Funktionen sind (Funktionalanalysis)so genannte Funktionaleerweitert. Darüber hinaus findet sie Anwendung in der Geometrie (Differentialgeometrie) bzw. mit einem erweiterten Integralbegriff in der Wahrscheinlichkeitsrechnung (Maßtheorie). Außerhalb der Mathematik wird die Analysis in allen Bereichen angewandt, in denen kontinuierliche Prozesse eine Rolle spielen, wobei sie vor allem engste Beziehungen zur Physik aufweist.
Der Grundbegriff der Analysis ist der des Grenzwertes (von Folgen, Reihen und Funktionen). Damit wurden seit Mitte des 19. Jahrhunderts nicht nur der Stetigkeits- und Differenzierbarkeitsbegriff für reelle Funktionen in strenger Form (durch Bolzano, Cauchy und Weierstraß) gefasst, sondern auch den der reellen Zahlen selbst (durch Dedekind und Cantor).
Die wichtigsten Zahlen der Mathematik, wie die Eulersche Zahl e oder die Kreiszahl p, können überhaupt nur über einen Grenzwert von Folgen oder Reihen definiert und näherungsweise berechnet werden. Auch die neben den Polynomen und gebrochen rationalen Funktionen wichtigsten Funktionen der Analysis werden entweder als Reihen von Folgen mit variablen Gliedern (die Exponentialfunktion exp, die trigonometrische Funktionen sin und cos) oder als Integral bzw. als Umkehrfunktionen (die Logarithmus-Funktion log bzw. arcsin und arccos) definiert.
Die einfachste Folge ist die geometrische Folge, die für eine reelle Zahl q durch \(a_0 =1\) und \(a_{n+1} = a_n\cdot q\) für n = 0, 1, 2,definiert wird. Wegen \(q^0=1\) gilt dann \(a_n = q^n\) für alle n. Ist -1 < q < 1, so konvergiert die Zahlenfolge an gegen den Grenzwert a = 0; man schreibt
\($ \lim_{n \to \infty }a_n=0 $\)
und nennt a den Limes der Folge.
Für q = 1 ist 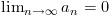 und für q = -1 nimmt an abwechselnd die Werte -1 und 1 an.
und für q = -1 nimmt an abwechselnd die Werte -1 und 1 an.
Ist q > 1, so wächst die Folge über alle Grenzen.
Jeder Folge an kann eine neue Folge, die Folge ihrer Partialsummen, zugeordnet werden:
\(s_n=a_0+a_1+a_2+a_3+. . . +a_n\). Eine solche Folge von Partialsummen nennt man eine unendliche Reihe und bezeichnet im Fall der Konvergenz den Grenzwert \(s = \lim_{n \to \infty } s_n\) mit \(\sum_{n=0}^{\infty }a_{n}\)
Für die geometrische Reihe, die Folge der Partialsummen der geometrischen Folge qn gilt s = \(\sum_{n=0}^{\infty }q^{n}=\frac{1}{1-q}\) und speziell s = 2 für \(q=\frac{1}{2}\) .
Wenn man die Kehrwerte der natürlichen Zahlen addiert, erhält man die harmonische Reihe \(\sum_{n=1}^{\infty }\frac{1}{n}\) .
Dass diese unendliche Reihe nicht konvergiertman sagt sie sei divergent ", hat bereits um 1350 der französische Bischof Nicole Oresme erkannt.
Eine Funktion ist eine Zuordnung, die jedem Element x einer Definitionsmenge D genau ein Element y einer Zielmenge Z zuordnen.
Man schreibt f: D Z, xy oder y = f (x), falls die Zuordnung von x zu y durch eine Funktionsgleichung beschrieben werden kann. Auf diese Weise können die unterschiedlichsten Funktionen definiert werden. Die Palette reicht von der Parabel y = f(x) = x² oder deren Verallgemeinerungen den Polynomen mit dem Funktionsterm
\(f(x) = x^n + a_{n-1}x^{n-1}+...+ a_1x + a_0\)
über die gebrochen rationalen Funktionen, von denen die einfachste die Hyperbel \(y=f(x)=\frac{1}{x}\) mit dem Definitionsbereich D = {\(x\in \mathbb{R}\) | x0} ist, bis zu exotischen Funktionen wie etwa der Dirichlet-Funktion, die durch die Funktionsgleichung
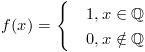
gegeben ist.
Die letzten beiden Funktionen sind unstetige Funktionen, wenn man die Hyperbelfunktion durch die Festsetzung f(0) =0 zu einer Funktion auf \(\mathbb{R}\) erweitert. Dabei versteht man unter einer stetigen Funktion anschaulich eine Funktion, deren Graph sich ohne Absetzen des Bleistifts zeichnen lässt, d.h., dass sie keine Sprungstellen besitzt. Es gibt verschiedene Möglichkeiten den Begriff der Stetigkeit zu definieren, am einfachsten ist der folgende. Eine Funktion f ist stetig in einem Punkt \(x_0\) ihres Definitionsbereichs, wenn sich bei Annäherung an \(x_0\) die Funktionswerte f(x) dem Funktionswert \(f(x_0)\) nähern:
\(\lim_{x \to x_0}f(x)=f(x_0)\).
Beispielsweise ist die kubische Funktion \(f(x) = x^3 + 2x^2 - 7x \) (und allgemeiner jedes Polynom) eine stetige Funktion, während die auf \(\mathbb{R}\) erweiterte Hyperbelfunktion im Punkt \(x_0=0\) nicht stetig ist: für negative Werte nahe bei 0 werden die Funktionswerte beliebig klein, während sie für positive Werte nahe 0 beliebig groß werden
\((f(\frac{-1}{0,001})=-1000\) und \(f(\frac{1}{0,001})=1000)\).
Außerhalb des Nullpunkts ist sie jedoch stetig, während die Dirichlet-Funktion in keinem Punkt stetig ist. Die Stetigkeit der Polynome ergibt sich aus der Tatsache, dass eine Summe und Produkte stetiger Funktionen wieder stetig ist. Es ist also nur zu zeigen, dass die Potenzfunktionen stetig sind. Im Fall \(f(x)=x^3\) muss man \(x^3\) und \(x_0^3\) vergleichen. Mit Hilfe von Polynomdivision (oder durch Ausmultiplizieren) sieht man:
\(x^3-x_{0}^{3} = (x-x_0)(x^2 + xx^0 + x_{0}^{2}\))
Hier nähert sich der zweite Faktor dem Wert \(3x_0^2\) wenn x gegen \(x_0\) strebt, das Produkt nähert sich also dem Wert 0:
\(\lim_{x \to x_0}x^3=x_{0}^{3}\).
Die meisten der in der Schule betrachteten Funktionen sind differenzierbar, sie besitzen in jedem Punkt ihres Definitionsbereichs eine Ableitung bzw. in jedem Punkt ihres Graphen eine Tangente, deren Steigung die Ableitung liefert. Wird jedem x-Wert einer differenzierbaren Funktion f dieser Steigungswert zugeordnet, so entsteht eine neue Funktion, die Ableitungsfunktion f?. Zur Berechnung der Ableitung \(f'(x_0)\) betrachtet man die Steigungen der Sekanten durch \((x_0|f(x_0))\) und benachbarte Punkte \((x|f(x))\) und bestimmt den Grenzwert für \(x \to x_0\):
\(f'(x_0)= \lim_{x \to x_0,x\neq x_0}\frac{f(x)-f(x_0)}{x-x_0}\)
Wie gerade gesehen ist die Ableitung von \(f(x) = x^3\) gegeben durch\(f'(x) = 3x^2 \). Etwas komplizierter ist es zu zeigen, dass beispielsweise
\(sin' (x) = cos (x)\) und \(exp'(x) = e^x\) gilt (wobei \(exp(x) = e^x\)).
Alle differenzierbaren Funktionen sind auch stetig. Es gilt aber nicht die Umkehrung. Die Betragsfunktion mit f(x) = |x| ist stetig, hat aber im Nullpunkt keine Tangente.
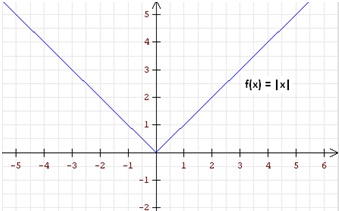
Die Ableitung einer Funktion gibt Aufschluss über deren Eigenschaften und damit über den Verlauf des Funktionsgraphen. Mit ihrer Hilfe kann man die Nullstellen approximieren (Newton-Verfahren) sowie Extremwerte und Wendepunkte berechnen, kurz: die Funktion diskutieren. Unter dem Stichwort "Kurvendiskussion" lassen sich auch ebene Kurven untersuchen, die nicht oder nur in Teilen durch einen Funktionsgraph beschrieben werden können. Hierzu gehören etwa die Kegelschnitte (Kreis \(x^2 + y^2 = r^2\), Ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), Parabel \(y^2 = ax+b\)) oder höhere algebraische und transzendente Kurven (kubische Parabeln, kartesisches Blatt, Lemniskate, Zykloide, Spirale usw.)
Praktische Anwendungen bieten die Extremwertaufgaben, beispielsweise etwa:
Wie kann man aus einem 36 cm langen Draht den Rahmen einer quadratischen Säule mit möglichst großem Volumen herstellen.
Dazu muss man wissen, dass sich das Volumen einer quadratischen Säule mit der Grundseite a und der Höhe h nach der Formel V=a²?h berechnet. Gegeben ist die Gesamtkantenlänge K (36 cm), die sich ebenfalls durch a und h ausdrücken lässt: K = 8a + 4h. Setzt man hier den Wert 36 ein und löst nach h auf, so wird 4h = 368a oder
h = 92a. In die Volumenformel eingesetzt erhält man V als Funktion von a: V(a) = a²(92a) = 9a²2a³.
Da das Volumen stets positiv ist, kann a nur Werte zwischen 0 und \(\frac{9}{2}\) annehmen. In diesem Intervall ist das Maximum der Funktion zu suchen. Man bestimmt die Ableitung von V und setzt diese gleich 0: V?(a) = 18a6a² = 0. Daraus folgt 18a = 6a² oder a = 3. Da die zweite Ableitung V??(a) für a = 3 negativ ist, liegt tatsächlich ein Maximum vor. Man berechnet noch h = 93?3 = 3 und erhält als größtmögliches Volumen V=27 cm³.
In engem Zusammenhang mit der Differenzalrechnung steht die Integralrechnung, die historisch der Differenzialrechnung sogar vorausging. Bereits Archimedes hat die Fläche krummlinig begrenzter ebener Figuren bestimmt (Parabelabschnitte und Kreis). Auch dabei spielen Grenzwerte die Hauptrolle. Dem Kreis wird ein regelmäßiges Vieleck einbeschrieben, dessen Fläche man durch Zerlegen in Dreiecke berechnen kann. Die Fläche des Kreises ergibt sich dann als Grenzwertz der Vieleckflächen, wenn deren Seitenzahl immer weiter verdoppelt wird. Der direkte Zusammenhang zwischen Differenzial- und Integralrechnung wurde unter anderem von Leibniz erkannt. Der Flächeninhalt der Figur, die durch den Graph einer positiven Funktion f und der x-Achse über einem Intervall [a,b] festgelegt wird , ist gegeben durch das Integral
\(\int_{b}^{b}f(x)dx\).
Hat man eine Stammfunktion von f, d.h. eine differenzierbare Funktion F mit F' = f, so lässt sich diese Integral leicht berechnen. Es gilt der Hauptsatz der Differenzial- und Integralrechnung:
\(\int_{b}^{b}f(x)dx=F(b)-F(a)\).
Außer Flächen lassen sich auch Volumina von Rotationskörper mit Hilfe der Integralrechnung berechnen.

