Additionsverfahren zum Lösen linearer Gleichungssysteme
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit dem Additionsverfahren lineare Gleichungssysteme mit zwei Variablen lösen kannst.
Lösen von linearen Gleichungssystemen
Du kannst zum Lösen von Gleichungssystemen mit zwei linearen Gleichungen das Additionsverfahren nutzen.
Die beiden Gleichungen kannst du jeweils im Waagemodell betrachten. Beide Waagen befinden sich im Gleichgewicht.
Wenn du die Inhalte der linken Seiten und die Inhalte der rechten Seiten gemeinsam auf die entsprechenden Seiten einer Waage legst, erhältst du wieder ein Gleichgewicht.
Die Summe der Terme der linken Seiten der Gleichungen ist also genauso groß wie die Summe der Terme der rechten Seiten der Gleichungen.
Ziel dieses Verfahrens ist, eine Gleichung zu erhalten, die nur noch eine Variable enthält.
Eine Variable fällt weg, wenn der Koeffizient einer Variablen in einer Gleichung die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung ist.
Die Koeffizienten sind Gegenzahlen
Löse folgendes Gleichungssystem in ℚ:

Gleichungen addieren
Achte darauf, dass die Variablen in den Gleichungen untereinander stehen.
Der Koeffizient von x in der ersten Gleichung (6) ist die Gegenzahl des Koeffizienten von x in der zweiten Gleichung (-6).
Um die Terme mit x zu eliminieren, brauchst du also nur die Gleichungen zu addieren.
Anzahl der Lösungen bestimmen
Du löst die Gleichung
:
 Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutigen Wert erhältst.
Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutigen Wert erhältst.
Wie viele Lösungen hat das Gleichungssystem in ℚ?


Lösungen berechnen
Du hast y bereits im vorigen Schritt berechnet. Um x zu berechnen, setzt du
in eine der Ausgangsgleichungen ein:
 Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.
Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.

 Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.
Du kannst dein Ergebnis anhand der zweiten Gleichung überprüfen. Ist die Lösung richtig, erhältst du hier das gleiche Ergebnis.

y = 2 und x =
Lösungsmenge bestimmen
Das Zahlenpaar
und
löst die Gleichung.
Du schreibst die Lösung (in runden Klammern) als Zahlenpaar
. Du schreibst für die Lösungsmenge kurz L = { 1 2 ; -6 }.
L = { 1 2 ; 2 }
Koeffizienten sind gleich - Multiplikation mit -1
Durch das Addieren zweier Gleichungen erhältst du nicht immer sofort eine Gleichung mit einer Variablen. Du kannst die Gleichungen so umformen, dass bei einer der Variablen der Koeffizient in der einen Gleichung die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung ist.
Wenn die Koeffizienten derselben Variablen in beiden Gleichungen gleich sind, multiplizierst du eine der Gleichungen mit -1.
Löse folgendes Gleichungssystem in ℚ:



Multiplizieren
In der Gleichung ist kein Koeffizient einer Variablen die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung.
Die Koeffizienten von x haben hier jedoch in beiden Gleichungen den gleichen Wert. Du multiplizierst eine der beiden Gleichungen mit -1, sodass du die Koeffizienten 3 und -3 erhältst.

Gleichungen addieren
Jetzt kannst du die Gleichungen addieren.
Die Variable x fällt weg 3 x + -3 x = 0 und du kannst y berechnen.

Anzahl der Lösungen bestimmen
Du löst die Gleichung
:
 Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutigen Wert erhältst.
Das Gleichungssystem hat genau eine Lösung, da du für y einen eindeutigen Wert erhältst.
Wie viele Lösungen hat das Gleichungssystem in ℚ?


Lösungsmenge bestimmen
Du hast y bereits im vorigen Schritt berechnet. Um x zu berechnen, setzt du y = -2 in eine der Ausgangsgleichungen ein: Die Probe bestätigt das Ergebnis:
Die Probe bestätigt das Ergebnis:
 Die Probe bestätigt das Ergebnis:
Die Probe bestätigt das Ergebnis:
L = {(5;-2)}
Koeffizienten sind ungleich
Du formst die Gleichungen so um, dass bei einer Variablen der Koeffizient in der einen Gleichung die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung ist. Dazu kannst du das kleinste gemeinsame Vielfache (kgV) der Koeffizienten einer Variablen in beiden Gleichungen verwenden.
Löse folgendes Gleichungssystem in ℚ:


Multiplizieren
In der Gleichung ist kein Koeffizient einer Variablen die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung.
Da der Koeffizient 15 von y in Gleichung II (-15) ein Vielfaches des Koeffizienten 3 von y in Gleichung I ist, ist es sinnvoll, die Gleichung I mit 5 zu multiplizieren, denn
und 15 ist die Gegenzahl von -15.

Lineares Gleichungssystem lösen
Du addierst beide Gleichungen:  Du berechnest x:
Du berechnest x: Das Gleichungssystem hat genau eine Lösung.
Du setzt den Wert für x in eine Ausgangsgleichung ein und erhältst den Wert für y:
Das Gleichungssystem hat genau eine Lösung.
Du setzt den Wert für x in eine Ausgangsgleichung ein und erhältst den Wert für y: 
 Du berechnest x:
Du berechnest x:
L={(2;1)}
Koeffizienten sind ungleich
Löse folgendes Gleichungssystem in ℚ:


Multiplizieren
In der Gleichung ist kein Koeffizient einer Variablen die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung. Du erweiterst beide Gleichungen so, dass ein Koeffizient der einen Variablen die Gegenzahl des Koeffizienten derselben Variablen in der anderen Gleichung ist.
Das kleinste gemeinsame Vielfache der Koeffizienten von y ist
.
Du multiplizierst die Gleichungen jeweils so, dass 12 und -12 die neuen Koeffizienten von y sind:

Lineares Gleichungssystem lösen
Du addierst beide Gleichungen:  Du berechnest x:
Du berechnest x: Das Gleichungssystem hat also genau eine Lösung.
Du setzt den Wert für x in beide Ausgangsgleichungen ein:
Das Gleichungssystem hat also genau eine Lösung.
Du setzt den Wert für x in beide Ausgangsgleichungen ein: 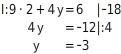
 Du erhältst in beiden Gleichungen dasselbe Ergebnis für y und damit das Wertepaar
als Lösung.
Du erhältst in beiden Gleichungen dasselbe Ergebnis für y und damit das Wertepaar
als Lösung.
 Du berechnest x:
Du berechnest x: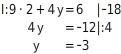
 Du erhältst in beiden Gleichungen dasselbe Ergebnis für y und damit das Wertepaar
als Lösung.
Du erhältst in beiden Gleichungen dasselbe Ergebnis für y und damit das Wertepaar
als Lösung.
L={(2;-3)}
Anzahl der Lösungen
Bei linearen Gleichungssystemen gibt es drei verschiedene Möglichkeiten für die Anzahl der Lösungen:

keine Lösung
Löse folgendes Gleichungssystem in ℚ:

Lösung bestimmen
Du addierst die Gleichungen:
 Das Gleichungssystem hat keine Lösung, da bei der Addition der Gleichungen eine falsche Aussage entsteht:
Die Lösungsmenge ist leer: L={ }
Das Gleichungssystem hat keine Lösung, da bei der Addition der Gleichungen eine falsche Aussage entsteht:
Die Lösungsmenge ist leer: L={ }
 Das Gleichungssystem hat keine Lösung, da bei der Addition der Gleichungen eine falsche Aussage entsteht:
Die Lösungsmenge ist leer: L={ }
Das Gleichungssystem hat keine Lösung, da bei der Addition der Gleichungen eine falsche Aussage entsteht:
Die Lösungsmenge ist leer: L={ }
Wie viele Lösungen hat das Gleichungssystem in ℚ?


unendlich viele Lösungen
Löse folgendes Gleichungssystem in ℚ:

Lösung bestimmen
Du löst das lineare Gleichungssystem:
 Das Gleichungssystem hat unendlich viele Lösungen, da bei der Addition der Gleichungen eine Aussage entsteht, die unabhängig von x stets wahr ist:
Für jeden x-Wert in ℚ erhältst du nach Einsetzen in die Gleichungen genau einen Wert für y.Durch Umstellen einer der beiden Ausgangsgleichungen erhältst du:
Es ergibt sich folgende Lösungsmenge: L = {
Das Gleichungssystem hat unendlich viele Lösungen, da bei der Addition der Gleichungen eine Aussage entsteht, die unabhängig von x stets wahr ist:
Für jeden x-Wert in ℚ erhältst du nach Einsetzen in die Gleichungen genau einen Wert für y.Durch Umstellen einer der beiden Ausgangsgleichungen erhältst du:
Es ergibt sich folgende Lösungsmenge: L = { x ; 4 - 3 x |x ∈ ℚ}
 Das Gleichungssystem hat unendlich viele Lösungen, da bei der Addition der Gleichungen eine Aussage entsteht, die unabhängig von x stets wahr ist:
Für jeden x-Wert in ℚ erhältst du nach Einsetzen in die Gleichungen genau einen Wert für y.Durch Umstellen einer der beiden Ausgangsgleichungen erhältst du:
Es ergibt sich folgende Lösungsmenge: L = {
Das Gleichungssystem hat unendlich viele Lösungen, da bei der Addition der Gleichungen eine Aussage entsteht, die unabhängig von x stets wahr ist:
Für jeden x-Wert in ℚ erhältst du nach Einsetzen in die Gleichungen genau einen Wert für y.Durch Umstellen einer der beiden Ausgangsgleichungen erhältst du:
Es ergibt sich folgende Lösungsmenge: L = {
Wie viele Lösungen hat das Gleichungssystem in ℚ?



