Lösen von Gleichungen durch Äquivalenzumformungen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du Gleichungen systematisch mit Hilfe von äquivalenzumformungen lösen kannst und wie du überprüfst, ob die Lösung richtig ist.
äquivalente Gleichungen
Zwei Gleichungen sind
, wenn sie dieselbe
haben.
Die Gleichungen 3x + 7 = 16 und x = 3 sind äquivalent, denn beide Gleichungen haben die Lösungsmenge L = {3}.
Die Gleichungen 3x + 7 = 16 und 3x + 6 = 15 sind äquivalent, denn beide Gleichungen haben die Lösungsmenge L = {3}.
Die Gleichungen 3x + 7 = 16 und 3x + 6 = 16 sind nicht äquivalent, denn die Lösungsmengen sind verschieden:
= {3} und
= {
}.
Gleichungen lösen durch äquivalenzumformungen
Durch äquivalenzumformungen kannst du Gleichungen verändern, ohne deren Lösungsmenge zu ändern. Du kannst äquivalenzumformungen also nutzen, um eine Gleichung zu lösen.Man sagt dann, dass die Variable durch diese Umformungen isoliert wird, bzw. die Gleichung nach der Variablen „aufgelöst“ wird.Folgende Umformungen verändern die Lösungsmenge einer Gleichung nicht, sind also äquivalenzumformungen:
•Addition oder Subtraktion der gleichen Zahl oder des gleichen Terms auf beiden Seiten der Gleichung.•Multiplikation auf beiden Seiten mit einer von Null verschiedenen Zahl.•Division auf beiden Seiten durch eine von Null verschiedene Zahl.
Jede Termvereinfachung auf beiden Seiten, wie zum Beispiel Klammern Auflösen oder Zusammenfassen gleichartiger Terme, ändert die Lösungsmenge der Gleichung nicht.Beim schrittweisen Lösen einer Gleichung durch äquivalenzumformungen wird der Umformungsschritt hinter einem senkrechten Strich angegeben.
Welche äquivalenzumformung wurde hier durchgeführt?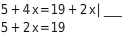
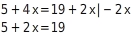
Umformungsschritt angeben
Auf beiden Seiten hat sich der Term mit x verändert. Auf der linken Seite wurde aus dem Term 4x der Term 2x und auf der rechten Seite fehlt der Term 2x. Die Terme ohne x sind unverändert.
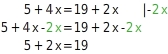
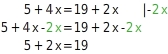
Löse die Gleichung mit Hilfe der äquivalenzumformungen.
Gleichung äquivalent umformen
Probe
Das Einsetzen der errechneten Lösung x = -1 ergibt auf beiden Seiten der Gleichung den Wert 3. x = -1 ist die Lösung der Gleichung
.
Linke Seite:
rechte Seite:
Angabe der Lösungsmenge
L = {-1}
äquivalenzumformungen am Waagemodell
äquivalenzumformungen lassen sich am Waagemodell darstellen.
Der Inhalt der Waagschalen darf nur so geändert werden, dass die Waage immer im Gleichgewicht bleibt. Das Ziel ist es, dass ein einzelnes x auf der rechten oder linken Waagschale alleine steht.
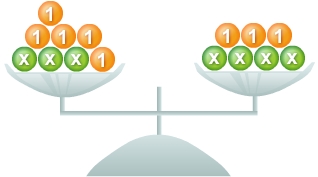Welche Gleichung wird an der Waage dargestellt" Gib die Lösungsmenge an.
Gleichung aufstellen
Lösen der Gleichung durch äquivalenzumformungen
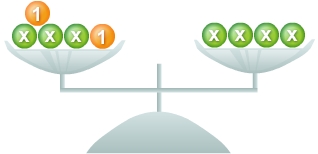
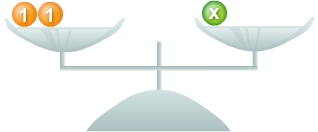
Probe
Das Einsetzen der errechneten Lösung x = 2 ergibt auf beiden Seiten der Gleichung den Wert 11. x = 2 ist die Lösung der Gleichung 5 + 3x = 4x + 3.
Linke Seite: 5 + 3 • 2 = 11 rechte Seite: 4 • 2 + 3 = 11
Angabe der Lösungsmenge
L = {2}
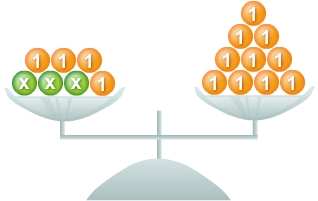Welche Gleichung wird an der Waage dargestellt" Gib die Lösungsmenge an.
Gleichung aufstellen
Lösen der Gleichung durch äquivalenzumformungen
Probe
Das Einsetzen der errechneten Lösung x = 2 ergibt auf beiden Seiten der Gleichung die Lösung 10. x = 2 ist die Lösung der Gleichung 4 + 3x = 10.
Linke Seite: 4 + 3 • 2 = 10 rechte Seite: 10
Angabe der Lösungsmenge
L = {2}
Besondere Lösungsmengen
Ist eine Gleichung immer lösbar" Hat eine Gleichung immer nur eine Lösung?Eine lineare Gleichung hat in einer vorgegebenen Grundmenge entweder ...-keine Lösung (dann ist sie nicht lösbar),-eine Lösung oder-unendlich viele Lösungen.
Löse die Gleichung
in der Grundmenge ℕ.
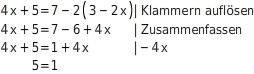
Gleichung äquivalent umformen
Diese Gleichung „endet“ in einer falschen Aussage unabhängig von der Variablen x und der Grundmenge ℕ. Das bedeutet, dass es keine Zahl gibt, die aus dieser Gleichung eine wahre Aussage macht.Die Gleichung ist nicht lösbar.
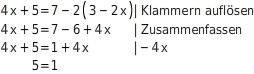
Angabe der Lösungsmenge
Die Mengenklammer für die Lösungsmenge ist leer, da es KEINE Zahl gibt, die Gleichung lösen kann.
L = {}
Löse die Gleichung
in der Grundmenge ℤ.
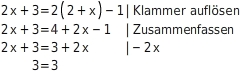
Gleichung äquivalent umformen
Diese Gleichung „endet“ in einer wahren Aussage unabhängig von der Variablen x und der Grundmenge ℤ. Das bedeutet, dass jede Zahl aus ℤ die Gleichung zu einer wahren Aussage macht.Die Gleichung hat unendlich viele Lösungen.
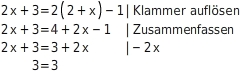
Angabe der Lösungsmenge
Als Lösungsmenge wird ℤ für den Zahlbereich der ganzen Zahlen angegeben. Das bedeutet, dass alle ganzen Zahlen die Gleichung lösen.
L = ℤ
Löse die Gleichung
in der Grundmenge ℕ.
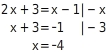
Gleichung äquivalent umformen
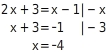
Angabe der Lösungsmenge
Diese Gleichung hat zwar ohne Beachtung der Grundmenge eine Lösung. Da aber -4 keine natürliche Zahl hat, ist die Gleichung in der Grundmenge ℕ nicht lösbar, die Lösungsmenge bleibt also leer.
L = {}
