Grafisches Lösen linearer Gleichungssysteme
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du lineare Gleichungssysteme mit zwei Variablen grafisch lösen kannst.
Lineare Gleichungssysteme
Zwei lineare Gleichungen mit zwei Variablen bilden ein lineares Gleichungssystem. Ein Zahlenpaar, das beide lineare Gleichungen erfüllt, wird Lösung des linearen Gleichungssystems genannt. Die linearen Gleichungen eines Gleichungssystems werden üblicherweise mit römischen Zahlen nummeriert (I und II).
Lösung eines linearen Gleichungssystems Prüfe, ob das Zahlenpaar (8;2) eine Lösung des linearen Gleichungssystems ist. 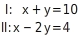
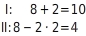
Werte einsetzen
Du setzt in die Gleichungen I und II für den Wert und für den Wert ein und überprüfst, ob sich für beide Gleichungen eine wahre Aussage ergibt. In diesem Beispiel entstehen aus beiden Gleichungen wahre Aussagen, also ist das Zahlenpaar ( ; ) eine Lösung des linearen Gleichungssystems: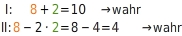
Lösung eines linearen Gleichungssystems Prüfe, ob das Zahlenpaar (4;2) eine Lösung des linearen Gleichungssystems ist. 
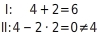
Werte einsetzen
Du setzt in die Gleichungen I und II für den Wert und für den Wert ein und überprüfst, ob sich für beide Gleichungen eine wahre Aussage ergibt. In diesem Beispiel entsteht nur bei der ersten Gleichung eine wahre Aussage. Die zweite Gleichung wird durch Einsetzen der Werte zu einer falschen Aussage. Somit ist das Zahlenpaar ( ; ) keine Lösung des linearen Gleichungssystems: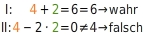
Grafisches Lösen von linearen Gleichungssystemen
Die Lösungen eines linearen Gleichungssystems mit zwei Variablen kannst du zeichnerisch bestimmen, indem du beide Gleichungen als Geradengleichungen auffasst und die zugehörigen Geraden in ein Koordinatensystem zeichnest. Es gibt drei Möglichkeiten für die Anzahl der Lösungen linearer Gleichungssysteme mit zwei Variablen:  Wie viele Lösungen ein Gleichungssystem hat, kannst du an der Lage der Geraden erkennen.
Wie viele Lösungen ein Gleichungssystem hat, kannst du an der Lage der Geraden erkennen. 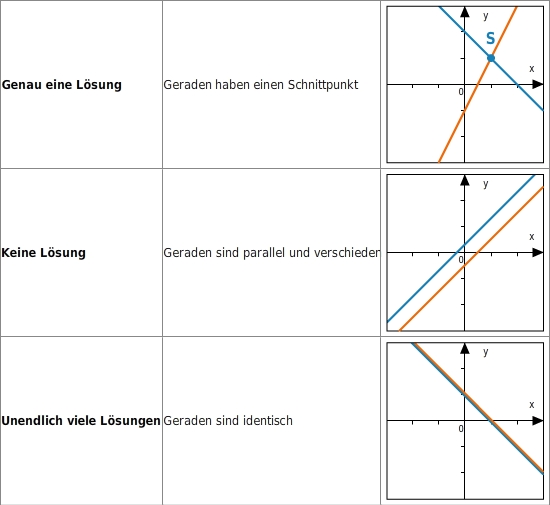

Grafisches Lösen eines linearen Gleichungssystems - genau eine Lösung Bestimme die Anzahl der Lösungen des linearen Gleichungssystems. Zeichne die zugehörigen Geraden in das Koordinatensystem. 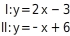

Geraden zeichnen
Zum Zeichnen der Geraden benötigst du zwei Punkte, die auf der Geraden liegen. Gerade I: Der y-Achsenabschnitt ist -3, du markierst also den Punkt . Einen weiteren Punkt erhältst du, wenn du z.B. einsetzt (du erhältst den Punkt ). Gerade II: Der y-Achsenabschnitt ist 6, du markierst also den Punkt . Einen weiteren Punkt erhältst du, wenn du z.B. einsetzt (du erhältst den Punkt ).

Anzahl der Lösungen bestimmen
Dieses lineare Gleichungssystem hat genau eine Lösung, da sich die Geraden im Punkt schneiden. Die Lösungsmenge L wird in geschweiften Klammern angegeben:L = { 3 ; 3 }
Wie viele Lösungen hat das Gleichungssystem in ℚ? 

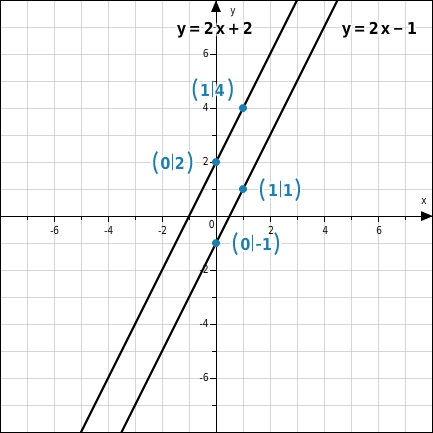
Grafisches Lösen eines linearen Gleichungssystems - keine Lösung Bestimme die Anzahl der Lösungen des linearen Gleichungssystems. Zeichne die zugehörigen Geraden in das Koordinatensystem.
Geraden zeichnen
Zum Zeichnen der Geraden benötigst du zwei Punkte, die auf der Geraden liegen. Gerade I: Der y-Achsenabschnitt ist -1, du markierst also den Punkt (0|-1). Einen weiteren Punkt erhältst du, wenn du z.B. einsetzt (du erhältst den Punkt (1|1)). Gerade II: Der y-Achsenabschnitt ist 2, du markierst also den Punkt (0|2). Einen weiteren Punkt erhältst du, wenn du z.B. einsetzt (du erhältst den Punkt (1|4)).

Anzahl der Lösungen bestimmen
Dieses lineare Gleichungssystem hat keine Lösung, da die Geraden parallel verlaufen. Die Geraden haben keinen gemeinsamen Punkt. Die Lösungsmenge L ist leer:L = { }
Wie viele Lösungen hat das Gleichungssystem in ℚ? 

Grafisches Lösen eines linearen Gleichungssystems - unendlich viele Lösungen Bestimme die Anzahl der Lösungen des linearen Gleichungssystems. Bringe dazu die beiden Gleichungen des linearen Gleichungssystems in Normalform und zeichne die zugehörigen Geraden ins Koordinatensystem.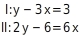
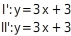
Gleichungen umstellen
Du stellst die Gleichungen jeweils nach um und erhältst damit zwei Geradengleichungen in Normalform: 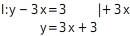
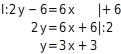
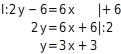
Anzahl der Lösungen bestimmen
Die beiden Geradengleichungen sind identisch. Die Geraden liegen also übereinander. Dieses lineare Gleichungssystem hat unendlich viele Lösungen, da die Geraden unendlich viele gemeinsame Punkte haben.
Wie viele Lösungen hat das Gleichungssystem in ℚ? 

Koeffizienten und Absolutglieder in linearen Gleichungssystemen
Bei einem lineare Gleichungssystem aus zwei Gleichungen kannst du die Anzahl der Lösungen mit Hilfe der Lage der zugehörigen Geraden zueinander bestimmen. Du betrachtest jeweils die Steigung und die y-Achsenabschnitte, die du den Normalformen der Geradengleichungen direkt entnehmen kannst: 

Veränderung der Koeffizienten - keine Lösung Für welchen Koeffizienten von hat das lineare Gleichungssystem keine Lösung" 
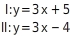
Koeffizienten bestimmen
Das lineare Gleichungssystem hat keine Lösung, wenn die zugehörigen Geraden parallel und verschieden sind. Das bedeutet, dass sie dieselbe Steigung haben. Der Koeffizient muss also 3 sein.
Veränderung des absoluten Gliedes - unendlich viele Lösungen Für welchen y-Achsenabschnitt hat das lineare Gleichungssystem unendlich viele Lösungen? 
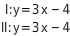
Absolutes Glied bestimmen
Das lineare Gleichungssystem hat unendlich viele Lösungen, wenn die zugehörigen Geraden identisch sind. Das bedeutet, dass die beiden Geradengleichungen gleich sein müssen. Der y-Achsenabschnitt ist also -4.
Veränderung des Koeffizienten - genau eine Lösung Für welchen Koeffizienten von hat das lineare Gleichungssystem genau eine Lösung? 



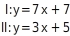

Koeffizienten bestimmen
Das lineare Gleichungssystem hat genau eine Lösung, wenn die Steigung der Geraden nicht gleich ist. Das bedeutet, dass hier jede von 3 verschiedene Zahl eingesetzt werden kann.
Veränderung des Koeffizienten mit Umstellen - keine Lösung Für welchen Koeffizienten von hat das lineare Gleichungssystem keine Lösung? 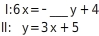
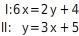
Koeffizient bestimmen
Das lineare Gleichungssystem hat keine Lösung, wenn die Steigung der zugehörigen Geraden gleich ist und die y-Achsenabschnitte verschieden sind. Du bringst die Gleichung I in Normalform: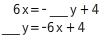 Im nächsten Schritt dividierst du durch den gesuchten Koeffizienten von . Aus Gleichung II weißt du, dass der Koeffizient von in Gleichung I auch 3 betragen muss. Die 3 erhältst du, wenn du durch dividierst:
Im nächsten Schritt dividierst du durch den gesuchten Koeffizienten von . Aus Gleichung II weißt du, dass der Koeffizient von in Gleichung I auch 3 betragen muss. Die 3 erhältst du, wenn du durch dividierst: 

