Eigenschaften linearer Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, welche Eigenschaften lineare Funktionen haben und wie du sie anhand ihrer graphischen Darstellung oder der Funktionsgleichung erkennen kannst.
Die Gerade als Graph einer linearen Funktion
Der Begriff linear leitet sich von lateinisch linea = "Leine, Schnur, Faden" ab. Der Graph einer linearen Funktion ist sozusagen eine "gespannte Leine", also eine Gerade.Den Graphen einer linearen Funktion kannst du von den Graphen anderer Funktionen unterscheiden.
Die Geraden f, g und q sind die Graphen linearer Funktionen.
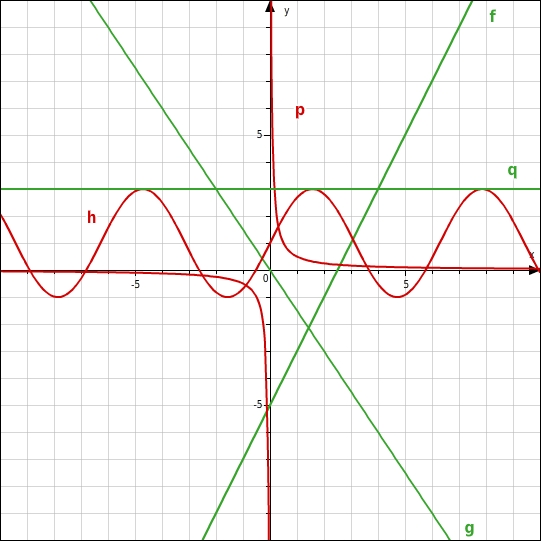
Die Graphen von f, g und q sind Geraden.Die Gerade q verläuft parallel zur x-Achse, jedem x-Wert wird der y-Wert 3 zugeordnet. Es handelt sich um den Graphen einer konstanten linearen Funktion.
Die Gerade k ist kein Graph einer linearen Funktion.
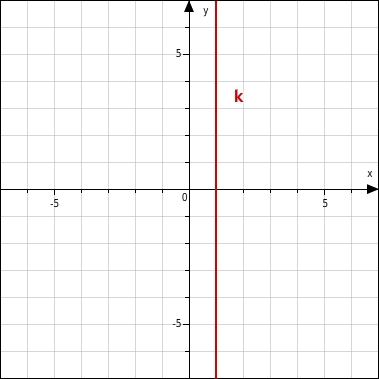
Die Gerade k verläuft parallel zur y-Achse, das bedeutet, dass dem x-Wert 1 unendlich viele y-Werte zugeordnet werden. Bei einer Funktion wird aber jedem x-Wert genau ein y-Wert zugeordnet.Die Gerade k hat die Gleichung
, das heißt, für jeden Punkt der Geraden erfüllt der x-Wert die Gleichung.
Die Funktionsgleichung einer linearen Funktion
Auch anhand der Funktionsgleichung kannst du lineare Funktionen von anderen unterscheiden.
Eine Kurve verläuft dann geradlinig, wenn sich bei gleichmäßiger Erhöhung (oder Verminderung) der x-Werte (Argumente) auch die y-Werte (Funktionswerte) gleichmäßig erhöhen (oder vermindern).
Das ist genau dann der Fall, wenn im Funktionsterm die Variable x nur mit einem Faktor (der Steigung) multipliziert wird. Dieser gibt an, wie stark die Funktionswerte zu- bzw. abnehmen, wenn sich x ändert.
Der Graph der Funktion f wird beschrieben durch die Geradengleichung
.
Immer wenn sich der Wert für x um 1 erhöht, erhöht sich der Funktionswert um 2, denn die Variable x wird mit 2 multipliziert.
Außerdem kann die Gleichung einen weiteren Summanden enthalten, das so genannte Absolutglied.
Dieses gibt an, an welcher Stelle die Gerade die y-Achse schneidet und wird daher auch y-Achsenabschnitt genannt.
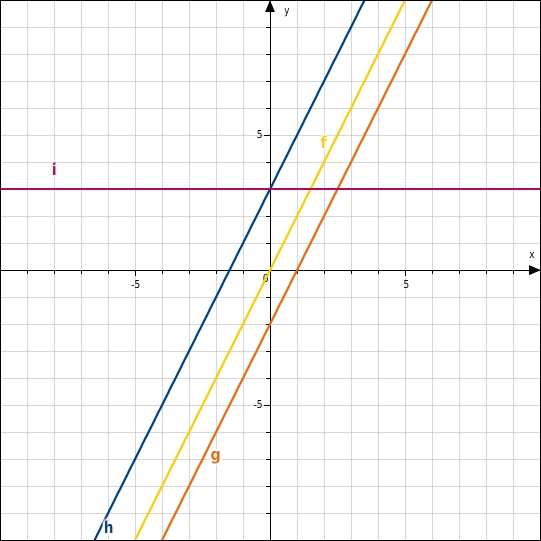
Die Graphen der Funktionen h, g und i werden beschrieben durch die Geradengleichungen:

Der Graph der Funktion h verläuft parallel zum Graphen der Funktion f und ist um 3 Einheiten nach oben verschoben.Der Graph der Funktion g verläuft parallel zum Graphen der Funktion f und ist um 2 Einheiten nach unten verschoben.Der Graph der Funktion i verläuft parallel zur x-Achse.
 Die Gleichung einer linearen Funktion hat immer die Gestalt
. Sie wird auch Normalform der Geradengleichung genannt.Dabei ist m die Steigung und b der y-Achsenabschnitt der Funktion.
Die Gleichung einer linearen Funktion hat immer die Gestalt
. Sie wird auch Normalform der Geradengleichung genannt.Dabei ist m die Steigung und b der y-Achsenabschnitt der Funktion.
Im Fall
ist die Steigung m = 2 und der y-Achsenabschnitt b = 0.Im Fall
ist die Steigung ebenfalls m = 2. Der y-Achsenabschnitt ist b = -2.Für den Fall
ist die Steigung m = 0 und der y-Achsenabschnitt b = 3.
Einfluss der Parameter m und b und Spezialfälle
Die Parameter m und b in der Funktionsgleichung
bestimmen den jeweiligen Verlauf des Graphen. Dabei ist m das Maß der Steigung und b bewirkt eine Verschiebung entlang der y-Achse.Je nach Belegung der Parameter m und b ergeben sich verschiedene Spezialfälle.
b = 0 ⇒
Der Graph der zugehörigen Funktion geht durch den Punkt 0 | 0 , egal, welchen Wert du für m einsetzt, denn
.Geraden durch den Koordinatenursprung heißen Ursprungsgeraden.
m = 0 ⇒
Der Graph der zugehörigen Funktion ist parallel zur x-Achse, denn für jedes x ist
.
m = 0 und b = 0 ⇒
Diese Gleichung beschreibt die x-Achse.
m = 1, b = 0 ⇒
Diese Gleichung beschreibt die Winkelhalbierende der Quadranten I und III, auch 1. Winkelhalbierende genannt.
m = -1, b = 0 ⇒
Diese Gleichung beschreibt die Winkelhalbierende der Quadranten II und IV, auch 2. Winkelhalbierende genannt.
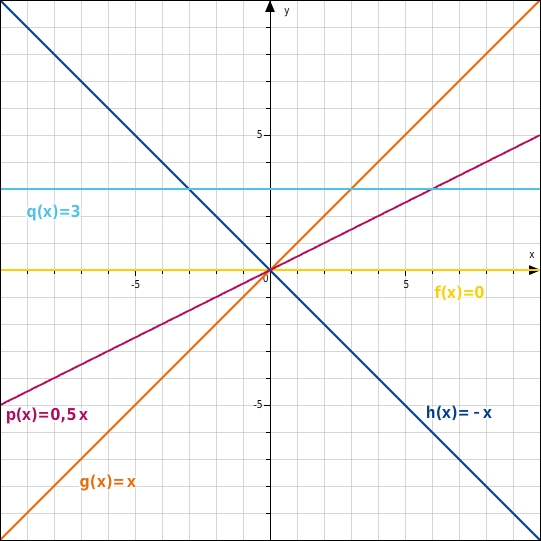
Die Abbildung zeigt alle diese Spezialfälle in einem Koordinatensystem.
Das Steigungsverhalten des Graphen einer linearen Funktion
Das Steigungsverhalten der Geraden hängt direkt vom Wert für m ab.- Je größer der Betrag von m ist, umso steiler verläuft die Gerade.- Je kleiner der Betrag von m ist, umso flacher verläuft die Gerade.- Ist m positiv, dann steigt die Gerade von links unten nach rechts oben.- Ist m negativ, dann fällt die Gerade von links oben nach rechts unten.
Gegeben sind die linearen Funktionen f, g, h und p mitf(x) =
,g(x) =
,h(x) =
undp(x) =
.
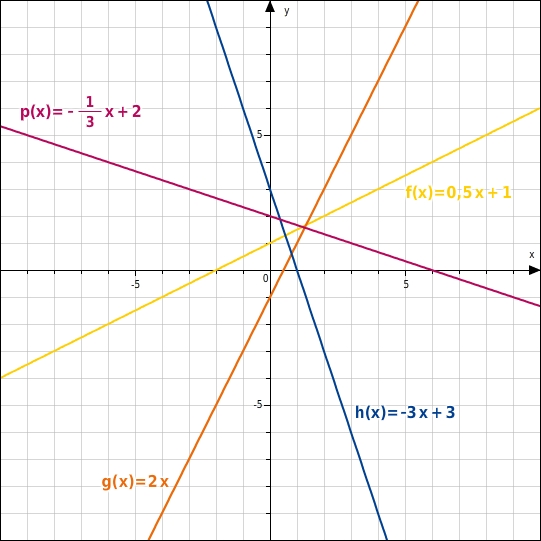 Wenn zwei Geradengleichungen denselben Wert für m und verschiedene y-Achsenabschnitte haben, dann haben die Geraden die gleiche Steigung, sie sind parallel.
Wenn zwei Geradengleichungen denselben Wert für m und verschiedene y-Achsenabschnitte haben, dann haben die Geraden die gleiche Steigung, sie sind parallel.
Wahre Aussagen auswählen
Du vergleichst die Koeffizienten von x miteinander.0
.5
2. Die Geraden f und g steigen und die Gerade f verläuft flacher als die Gerade g.-3
0 und -3
- 1 3 . Die Geraden h und p fallen und die Gerade p fällt flacher als die Gerade h.
Welche Aussagen sind wahr?


 Wenn zwei Geradengleichungen denselben Wert für m und verschiedene y-Achsenabschnitte haben, dann haben die Geraden die gleiche Steigung, sie sind parallel.
Wenn zwei Geradengleichungen denselben Wert für m und verschiedene y-Achsenabschnitte haben, dann haben die Geraden die gleiche Steigung, sie sind parallel.
Geradengleichungen in Normalform und in impliziter Form
Die Normalform der Geradengleichung
entspricht der Funktionsgleichung einer linearen Funktion. Mit Hilfe dieser Gleichung kannst du den Graphen der Funktion, also die Gerade, zeichnen, denn du kannst der Gleichung die wichtigen Parameter für die Gerade direkt entnehmen (m und b).Eine Geradengleichung kann aber auch in der sogenannten impliziten Form gegeben sein:
.
Dieser Gleichung kannst du die Steigung und den y-Achsenabschnitt nicht direkt entnehmen.
Gerade g



Wandle die Gleichung
in die Normalform um.
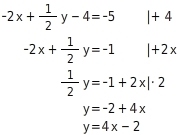
Normalform bestimmen
Du stellst die Gleichung in impliziter Form mit Hilfe der äquivalenzumformungen nach
um. Dabei wird allerdings b≠
vorausgesetzt:
⇔
Wenn
ist, erhältst du eine Parallele zur y-Achse. Die Gleichung ist dann nicht die Gleichung einer Funktion.
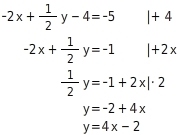
Lineare Funktionen in Sachsituationen
Viele Situationen im Alltag kannst du mit Hilfe linearer Funktionen beschreiben. Aber woran erkennst du das?Am häufigsten werden bei der verbalen Beschreibung Begriffe wie kontinuierlich, gleichmäßig, regelmäßig, täglich, wöchentlich usw. verwendet.
Lena hat in ihrem Sparschwein
und möchte ab sofort am Ende jeder Woche
sparen.Die Zuordnung Zeit in Wochen (x)  Summe im Sparschwein in Euro (f(x)) kann durch eine lineare Funktion beschrieben werden.
Summe im Sparschwein in Euro (f(x)) kann durch eine lineare Funktion beschrieben werden.
Herr Meier zahlt bei seinem Telefonanbieter eine Grundgebühr von
und für jede angefangene Gesprächsminute
.Die Zuordnung Anzahl der angefangenen Minuten (x)  Rechnungsbetrag in Euro (f(x)) kann durch eine lineare Funktion beschrieben werden.
Rechnungsbetrag in Euro (f(x)) kann durch eine lineare Funktion beschrieben werden.
Der Betrag auf Herrn Meiers Telefonrechnung steigt (fällt) gleichmäßig mit steigender (fallender) Anzahl der Gesprächsminuten.
Die Grundgebühr, ein Startguthaben oder ein beliebiger Anfangswert entsprechen immer dem y-Achsenabschnitt, denn das ist der Wert, der zum Zeitpunkt 0 oder bei 0 angefangenen Gesprächsminuten schon vorhanden war oder trotzdem gezahlt werden muss.

