Grundbegriffe zu Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, was eine Funktion ist und wie du sie beschreiben und darstellen kannst.
Zuordnungen und Funktionen
Zuordnungen spielen im täglichen Leben, in den Naturwissenschaften und natürlich in der Mathematik eine sehr wichtige Rolle.
Eine Zuordnung ist eine Beziehung, die - nicht notwendig allen - Elementen einer Ausgangsmenge jeweils ein oder mehrere Elemente einer Zielmenge zuordnet.
Es gibt verschiedene Möglichkeiten, Zuordnungen anzugeben.
Pfeildiagramm Das folgende Pfeildiagramm gibt die Zuordnung an, die vier Schülern (Sophie, Max, Lea, Leon) jeweils die Farbe ihres Fahrrades bzw. die Farben ihrer Fahrräder zuordnet.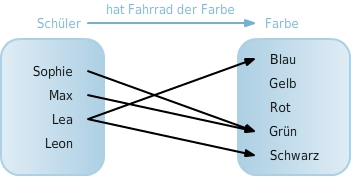 
Die Ausgangsmenge der Zuordnung besteht aus den Schülern. Die Zielmenge besteht aus Farben. Um zu verdeutlichen, dass eine Zuordnung zwischen den Schülern und Farben von Fahrrädern besteht, schreibt man kurz: Schüler → Farbe des Fahrrades Da Leon kein Fahrrad hat, kann ihm auch keine Farbe zugeordnet werden. Es beginnt kein Pfeil bei Leon. Sophies und Maxs Fahrrad haben die Farbe Grün. Bei Grün enden also zwei Pfeile. Da keiner der Schüler ein gelbes oder rotes Fahrrad hat, können Gelb bzw. Rot nicht zugeordnet werden. Es gibt somit weder einen Pfeil zu Gelb noch zu Rot. Lea hat zwei Fahrräder. Eins ist blau, das andere schwarz. Somit beginnen bei Lea zwei Pfeile.
Tabelle Im Lotto 6 aus 49 werden 6 Zahlen und eine Zusatzzahl nacheinander aus den natürlichen Zahlen von 1 bis 49 (ohne Zurücklegen) gezogen. Außerdem wird noch eine Superzahl aus den Ziffern 0 bis 9 gezogen. 
Es gibt 8 Gewinnklassen. Jede Gewinnklasse erhält einen bestimmten Anteil der Ausschüttungssumme, wobei dieser Anteil dann unter allen Gewinntipps dieser Klasse gleichmäßig aufgeteilt wird. Die folgende Tabelle gibt die Zuordnung an, die jeder Gewinnklasse den zugehörigen Ausschüttungsanteil zuordnet: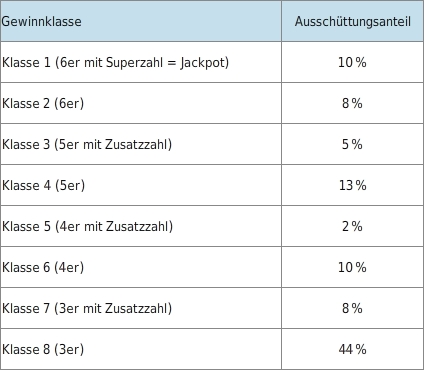 
Die Ausgangsmenge dieser Zuordnung besteht aus den Gewinnklassen. Die Zielmenge besteht aus den Ausschüttungsanteilen. Um deutlich zu machen, dass eine Zuordnung zwischen den Gewinnklassen und den Ausschüttungsanteilen besteht, schreibt man kurz: Gewinnklasse → Ausschüttungsanteil Diese Zuordnung hat zwei wichtige Merkmale: 
Aber beachte, dass zum Beispiel den Klassen 1 und 6 der gleiche Gewinnausschüttungsanteil ( ) zugeordnet ist.
Wenn du dich nur für einige einander zugeordnete Wertepaare interessierst, kannst du diese Wertepaare zusammengefasst in einer Menge angeben.
Menge von Wertepaaren Du kannst mit Hilfe einer Menge von Wertepaaren die zum Ausheben einer Grube benötigte Zeit in Stunden in Abhängigkeit von der Anzahl der beteiligten Arbeiter angeben. In den aufgeführten Wertepaaren bedeutet die vordere Zahl die Anzahl der beteiligten Arbeiter und die hintere Zahl die benötigte Arbeitszeit in Stunden: {(2; 12), (3; 8) , (4; 6) , (6; 4)}
Gelegentlich schreibt man einfach nur die Wertepaare ohne die Mengenklammern „{“ und „}“auf. Die Ausgangsmenge dieser Zuordnung besteht aus den in den Wertepaaren vorn stehenden Anzahlen von Arbeitern:{2; 3; 4; 6} Die Zielmenge besteht aus den jeweils zugeordneten Aushubdauern:{12; 8; 6; 4} Um deutlich zu machen, dass eine Zuordnung zwischen diesen beiden Mengen besteht, schreibt man kurz: Arbeiteranzahlen 
Aushubdauer
Aushubdauer Eine nicht allzu große Menge von Wertepaaren lässt sich sehr übersichtlich in einer Wertetabelle darstellen.
Wertetabelle Die zum Ausheben einer Grube benötigte Zeit in Stunden in Abhängigkeit von der Anzahl der beteiligten Arbeiter wurde im vorhergehenden Beispiel mit Hilfe einer Menge von Wertepaaren angegeben.Du kannst somit die Menge von Wertepaaren {(2; 12), (3; 8), (4; 6), (6; 4)} in einer Wertetabelle darstellen: 
Diese Zuordnung hat zwei wichtige Merkmale: 
Viele Zuordnungen haben zwei wesentliche Merkmale: 
Zuordnungen, die diese beiden Eigenschaften haben, nennt man Funktionen. In diesem Fall bezeichnet man die Ausgangsmenge als Definitionsbereich und die Zielmenge als Wertebereich.
Eine Funktion ist eine Zuordnung, die jedem Element des Definitionsbereichs jeweils genau ein Element des Wertebereichs zuordnet.
Beachte: 
Wenn du also einen Text über Funktionen liest, solltest du immer erst schauen, welche dieser Begriffe benutzt werden und wie sie definiert sind.
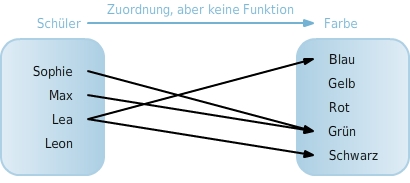
Das linke Pfeildiagramm stellt eine Zuordnung dar, die keine Funktion ist. Dem Schüler Leon ist gar keine Farbe zugeordnet. Somit kann diese Zuordnung keine Funktion sein. Außerdem sind der Schülerin Lea zwei Farben zugeordnet. Dies ist ein weiterer Grund, weshalb das linke Pfeildiagramm keine Funktion darstellt. Das rechte Pfeildiagramm hingegen stellt eine Funktion dar, denn jedem Schüler ist genau eine Farbe zugeordnet. Verschiedenen Schülern kann dieselbe Farbe zugeordnet werden. Zum Beispiel wird sowohl Sophie als auch Max die Farbe Grün zugeordnet. Entscheidend ist, dass keinem Schüler mehr als eine Farbe zugeordnet ist.
Ist die im Pfeildiagramm dargestellte Zuordnung eine Funktion? 
Funktionen erkennen
Dem Namen Leonie werden zwei Elemente (Steffen, Julian) zugeordnet. Somit ist die Zuordnung keine Funktion. Außerdem wird dem Namen Paul gar kein Element zugeordnet. Dies ist ein weiterer Grund, weshalb die Zuordnung keine Funktion ist.
Die Zuordnung ist keine Funktion.
Ist die im Pfeildiagramm dargestellte Zuordnung eine Funktion? 
Funktionen erkennen
Jedem Namen wird genau ein Element zugeordnet. Beachte:Verschiedenen Namen kann dasselbe Element (Bruder) zugeordnet werden. Zum Beispiel ist sowohl Sophie als auch Leonie der Bruder Steffen zugeordnet. Entscheidend ist, dass keiner Person mehr als ein Bruder zugeordnet ist. Außerdem können im Wertebereich Elemente sein, die gar nicht zugeordnet werden. In unserem Fall zum Beispiel Peter.
Die Zuordnung ist eine Funktion.
Welche Mengen von Wertepaaren stellen eine Funktion dar? 
Nur die Wertepaar-Mengen {(2; 3), (4; 7), (-2; 8), (5; 3), (1; 1)} und {(1; 3), (2; 4), (-4; 3), (-6; 3), (4; -3)} stellen Funktionen dar.Jedem vorderen Wert wird genau ein hinterer Wert zugeordnet. In den beiden anderen Fällen wird den Werten 3 bzw. 6 jeweils mehr als ein Wert zugeordnet. Die Zuordnungen sind in diesem Falle also mehrdeutig und stellen keine Funktionen dar.
Funktionen erkennen
Bei einer als Menge von Wertepaaren gegebenen Zuordnung bedeutet ein Wertepaar (zum Beispiel (2; 3)), dass der hintere Wert des Paares (3) dem vorderen Wert (2) zugeordnet ist. Nur in den beiden hervorgehobenen Fällen wird jedem vorderen Wert genau ein hinterer Wert zugeordnet. Also stellen nur dies beiden Fälle Funktionen dar.
Begriffe und Symbole bei Funktionen
Um Funktionen kurz und bündig angeben zu können, sind gewisse Schreibweisen und Bezeichnungen üblich.
Hier ist eine übliche Form, eine Funktion anzugeben: :[0;1] 
[2;3], 
, Bei dieser Schreibweise bedeutet :[0;1] 
[2;3], 
In der Regel haben Funktionen einen Namen. Oft sieht man die Buchstaben , oder als Namen. Selbstverständlich kannst du auch andere Buchstaben (klein oder groß), ganze Worte oder sonstige Zeichenkombinationen als Namen für Funktionen verwenden. 
, bedeutet 
In der Mathematik werden im Zusammenhang mit Funktionen die Werte aus dem Definitionsbereich sehr oft mit der Variablen x und die Werte aus dem Wertebereich mit der Variablen y bezeichnet. Dies ist keine feste Regel. Speziell in Sachzusammenhängen können auch andere Buchstaben an die Stelle von x bzw. y treten. Zum Beispiel steht t oft für die Zeit, v für die Geschwindigkeit, s für eine zurückgelegte Wegstrecke, T für die Temperatur, V für das Volumen, α für den Winkel u. v. m. 
Die Variable x heißt in diesem Zusammenhang Argument der Funktion. Da in der Mathematik das Argument einer Funktion häufig mit x bezeichnet wird, spricht man auch oft einfach vom x-Wert. Der Ausdruck heißt Funktionswert (von f an der Stelle x). Hier ist das der Wert, den du durch Einsetzen des x-Wertes in den Term berechnen kannst. Da in der Mathematik die Elemente des Wertebereichs einer Funktion häufig mit y bezeichnet werden, spricht man auch oft einfach vom y-Wert. Der Funktionsterm beschreibt also die Funktionswerte an jeder Stelle des Definitionsbereichs. In diesem Fall schreibt man statt 
auch 
f(x), Im Beispiel wäre das 
Dieser Ausdruck heißt Zuordnungsvorschrift. Da die Angabe von Funktionen nicht einheitlich ist, wirst du in verschiedenen Texten viele Kombinationen der eben erklärten Symbole und Abkürzungen sehen, wie zum Beispiel: ; : x 
y; : x 
f(x); : x 
u. v. m.
[2;3], , [2;3], , bedeutet f(x), y; f(x); Gegeben ist die Funktion : ℕ → ℚ mit aus ℕ, aus ℚ Ordne die Symbole und Terme den Begriffen zu. 
Symbole und Terme zuordnen
Der Definitionsbereich ist die Menge, die links vom Pfeil steht. Sie enthält alle Elemente, denen etwas zugeordnet werden soll. Der Wertebereich ist die Menge, die rechts vom Pfeil steht. Sie enthält mindestens alle Elemente, die zugeordnet werden. Die Zuordnungsvorschrift 
x - 2 gibt an, auf welche Weise jedem aus dem Definitionsbereich genau ein Element des Wertebereichs zugeordnet wird.
Gegeben ist die Funktion : 
mit 
x - 2 wobei aus ℕ und aus ℚ sind. Ordne die Symbole bzw. Terme den Begriffen zu. 
Symbole und Terme zuordnen
Der Funktionsterm x - 2 beschreibt, welche Rechnungen mit einem Element aus dem Definitionsbereich ausgeführt werden sollen. Den Ausdruck nennt man Funktionsgleichung. Als (Funktions-)Argument bezeichnet man die Variable , die für die Elemente des Definitionsbereichs verwendet wird. Der und der Funktionsterm x - 2 stimmen überein. Denn wenn du im Funktionsterm x - 2 die Variable durch eine Zahl ersetzt, wird dieser Zahl gerade der zugehörige Termwert von x - 2 zugeordnet.
Bestimme für die Funktion den Definitionsbereich und den Wertebereich.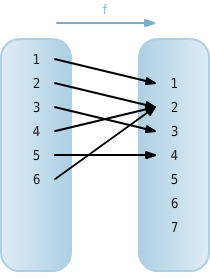 
Definitionsbereich bestimmen
Der Definitionsbereich besteht aus allen Elementen, denen durch die Zuordnungsvorschrift ein Element des Wertebereichs zugeordnet wird. Ist die Funktion mit einem Pfeildiagramm dargestellt, sind dies alle auf der linken Seite stehenden Elemente.
Wertebereich bestimmen
Der Wertebereich einer Funktion ist der angegebene Bereich, in dem die Funktionswerte liegen. Das heißt aber auch, dass der Wertebereich Elemente enthalten kann, die gar keine Funktionswerte sind. Bei einer Funktion, die mittels eines Pfeildiagramms dargestellt ist, besteht der Wertebereich aus allen Elementen des Bereiches, in den die Pfeile zeigen.
In vielen Texten werden der Definitionsbereich und der Wertebereich einer Funktion, die durch einen Funktionsterm, z. B. f(x), angegeben ist, nicht ausdrücklich erwähnt. In diesem Fall wählst du als Definitionsbereich alle diejenigen Werte, die du für x einsetzen kannst, um den zugehörigen Termwert f(x) zu berechnen. Als Wertebereich wählst du in so einem Fall die rationalen Zahlen ℚ. Beachte: Der Wertebereich einer Funktion muss mindestens alle durch die Funktion zugeordneten Funktionswerte enthalten. Jedoch enthält der Wertebereich oftmals viel mehr Werte als die durch die Funktion zugeordneten Funktionswerte.
Graphen von Zuordnungen und Funktionen
Bei unzähligen Zuordnungen bestehen sowohl die Ausgangs- als auch die Zielmenge aus Zahlen.Somit sind die Wertepaare, die die Zuordnung beschreiben, Zahlenpaare. Jedes Zahlenpaar kann auch als Koordinatenpaar aufgefasst und somit als Punkt im Koordinatensystem dargestellt werden.
In der Wertetabelle ist die zum Ausheben einer Grube benötigte Zeit (in Stunden) in Abhängigkeit von der Anzahl der beteiligten Arbeiter angegeben. 
Der Graph der in der Wertetabelle gegebenen Zuordnung ist im Koordinatensystem dargestellt: 
Jede Spalte in der Wertetabelle stellt ein Wertepaar da. Zum Beispiel stellt die erste Spalte das Wertepaar (2; 12) dar. Die Werte der oberen Zeile, also die jeweils vorderen Werte der Wertepaare, werden auf der waagerechten Achse abgetragen. Die Werte der unteren Zeile, also die jeweils hinteren Werte der Wertepaare werden auf der senkrechten Achse abgetragen.
In einer meteorologischen Station werden jeden Tag gemessene Werte für die Lufttemperatur aufgezeichnet.Hierbei handelt es sich um eine Zuordnung Uhrzeit → Temperatur.Der Graph des Temperaturverlaufs an einem bestimmten Tag von 0:00 Uhr bis 24:00 Uhr ist im Koordinatensystem dargestellt: 
Jeder Punkt auf dem Graphen beschreibt ein Wertepaar bestehend aus einer bestimmten Uhrzeit und der zu dieser Zeit registrierten Lufttemperatur. Auf der waagerechten Achse des Koordinatensystems wird die Uhrzeit abgetragen.Auf der senkrechten Achse die Lufttemperatur.
Sowohl die Menge der Wertepaare, die eine Zuordnung angeben, als auch deren graphische Darstellung in einem Koordinatensystem heißen Graph der Zuordnung. Wenn die Zuordnung eine Funktion ist, zum Beispiel die Funktionf: x 
y; y = f(x) = oder kurz f: x 
, besteht der Graph der Funktion f aus allen Wertepaaren (x;f(x)), also aus allen Wertepaaren (x; ), wobei x den Definitionsbereich der Funktion durchläuft. Man kann den Graphen einer Funktion f auch mit Hilfe der Funktionsgleichung y=f(x) angeben. Der Graph von f besteht aus allen Wertepaaren (x;y), die die Funktionsgleichung y=f(x) erfüllen.
y; y = f(x) = oder kurz f: x , besteht der Graph der Funktion f aus allen Wertepaaren (x;f(x)), also aus allen Wertepaaren (x; ), wobei x den Definitionsbereich der Funktion durchläuft. Der im Koordinatensystem dargestellte Graph der Funktion f(x) = entsteht, indem die Wertepaare (x ; f(x)) = (x ; ) als Punkte (x | f(x)) = (x | ) ins Koordinatensystem eingetragen werden. Zur Verdeutlichung sind die in der Wertetabelle angegebenen Wertepaare auf dem Graphen von f als Punkte hervorgehoben. 
Mit Hilfe der Funktionsgleichung y = f(x) kannst du einerseits feststellen, ob ein Wertepaar (x;y) auf dem Graphen der Funktion f liegt. Andererseits kannst du diese Gleichung auch benutzen, um unvollständige Wertepaare (x; __ ) bzw. ( __; y) so zu vervollständigen, dass das Wertepaar auf dem Graphen der Funktion f liegt. Ein Wertepaar (x;y) gehört zum Graphen der Funktion f, wenn das Wertepaar die Funktionsgleichung y = f(x) erfüllt. Das heißt, wenn du den x-Wert des Wertepaares in die Funktionsgleichung von f einsetzt, erhältst du den y-Wert des Wertepaares.
Gegeben ist die Funktionsgleichung . Ergänze die Wertepaare so, dass sie die Funktionsgleichung erfüllen. { (1; __ ); (4; __ ); ( __ ; -9 ); ( __ ; 3); (2; 1) }
Wertepaare vervollständigen
Beim den ersten beiden Wertepaaren ist jeweils der x-Wert gegeben. Du setzt also diese x-Werte in die Funktionsgleichung ein und ermittelst den jeweiligen zugehörigen y-Wert: (1; __ )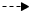 
: 
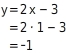(4; __ ) 
: 
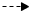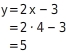Beim dritten und vierten Wertepaar ist jeweils der y-Wert gegeben. Du setzt also diese y-Werte in die Funktionsgleichung ein und ermittelst die jeweiligen zugehörigen x-Werte, indem du versuchst, nach x aufzulösen: (__; -9) 
: 
(__; 3)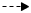 
: 
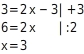
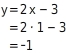
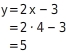
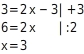
: : : : { (1; -1); (4; 5); (-3; -9); (3; 3); (2; 1) }
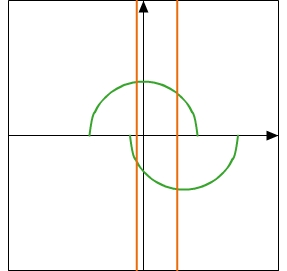
Am Graphen einer Zuordnung kannst du oft erkennen, ob die Zuordnung eine Funktion ist. Wenn im Koordinatensystem jede senkrechte Gerade den Graphen einer Zuordnung immer in höchstens einem Punkt schneidet, handelt es sich um den Graphen einer Funktion.
Graph einer Funktion: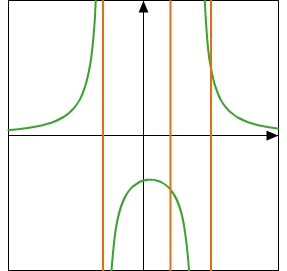 
Jede senkrechte Gerade schneidet den Graphen in höchstens einem Punkt. Der Definitionsbereich der abgebildeten Funktion besteht aus den Werten auf der waagerechten Achse, zu denen es Punkte auf dem Graphen gibt. Im obigen Bild erkennst du, dass alle Punkte auf einer senkrechten Geraden dieselbe Koordinate auf der waagerechten Achse haben. Eine Funktion ordnet jedem Wert des Definitionsbereichs genau einen Wert des Wertebereichs zu. Es kann also immer nur höchstens einen Punkt geben, der gleichzeitig auf einer senkrechten Geraden UND auf dem Graphen liegt. Beachte, dass der Graph einer Funktion aus mehreren Teilen bestehen kann und nicht unbedingt eine durchgehende Linie sein muss.
Kein Graph einer Funktion: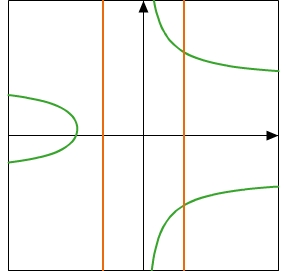 
Es gibt senkrechte Geraden, die den Graphen in mehr als einem Punkt schneiden.Dies kommt daher, da es Werte auf der horizontalen Achse gibt, denen mehr als ein Wert auf der vertikalen Achse zugeordnet sind.
Welcher Graph gehört zu einer Funktion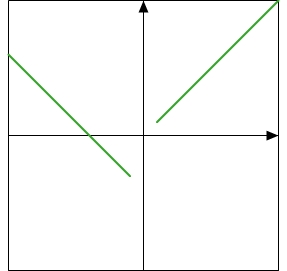 
Funktionen erkennen
Der Graph einer Funktion ist dadurch gekennzeichnet, dass jede senkrechte Gerade den Graphen höchstens einmal schneidet. Bei allen anderen Graphen gibt es vertikale Linien, die die Graphen in mehr als einem Punkt schneiden: 
