Kürzen und Erweitern von Brüchen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier findest du noch mal die wichtigsten Informationen zum Kürzen und Erweitern.
Erweitern eines Bruchs
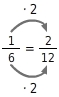
Du kannst einen Bruch erweitern, indem du Zähler und Nenner mit der gleichen Zahl multiplizierst. Beim Erweitern bleibt der vom Bruch dargestellte Anteil unverändert, dieser Anteil wird nur in kleinere Abschnitte unterteilt (die Einteilung wird verfeinert).
Erweitern
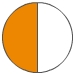
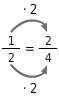
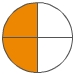
Erweitern
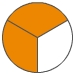
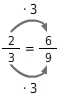

Kürzen eines Bruchs
Du kannst einen Bruch kürzen, indem du Zähler und Nenner durch die gleiche Zahl dividierst. Beim Kürzen bleibt der vom Bruch dargestellte Anteil unverändert, dieser Anteil wird nur in größere Abschnitte unterteilt (die Einteilung wird vergröbert).
Kürzen
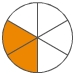
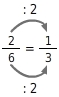
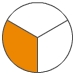
Kürzen



Erweiterungszahl
Die Zahl, mit der du einen Bruch erweiterst, ist die Erweiterungszahl. Die Erweiterungszahl findest du,indem du eine Ergänzungsaufgabe zu den beiden Zählern oder den beiden Nennern löst.
Ein Bruch kann nicht mit 0 erweitert werden.
Gib die Erweiterungszahl zu 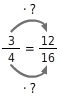 an.
an.

 an.
an.
Erweiterungszahl
Die Erweiterungszahl im Zähler ist 4, denn
.
Die Erweiterungszahl im Nenner ist 4, denn
.

Gib die Erweiterungszahl zu  an.
an.
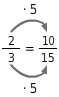
 an.
an.
Erweiterungszahl
Die Erweiterungszahl im Zähler ist 5, denn
.
Die Erweiterungszahl im Nenner ist 5, denn
.

Kürzungszahl
Die Zahl, mit der du einen Bruch kürzt, nennt man Kürzungszahl. Die Kürzungszahl findest du,indem du eine Ergänzungsaufgabe zu den beiden Zählern oder den beiden Nennern löst.
Ein Bruch kann nicht durch 0 gekürzt werden.
Gib die Kürzungszahl zu 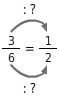 an.
an.

 an.
an.
Kürzungszahl
Die Kürzungszahl im Zähler ist 3, denn
.
Die Kürzungszahl im Nenner ist 3, denn
.

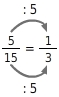
Gib die Kürzungszahl zu 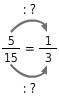 an.
an.
 an.
an.
Kürzungszahl
Die Kürzungszahl im Zähler ist 5, denn
.
Die Kürzungszahl im Nenner ist 5, denn
.

Kürzen mit dem größten gemeinsamen Teiler
Um so weit wie möglich zu kürzen, musst du den größten gemeinsamen Teiler (ggT) von Zähler und Nenner eines Bruchs finden. Der ggT ist die größte Zahl, mit der du einen Bruch kürzen kannst.
Kürze
so weit wie möglich:

Kürzen
Teiler von 18: {1, 2, 3,
, 9, 18}
Teiler von 24: {1, 2, 3, 4,
, 8, 12, 24}
Der größte gemeinsame Teiler von 18 und 24 ist
.

Auf den Hauptnenner erweitern
Der Hauptnenner ist der durch Erweitern von zwei oder mehr ungleichnamigen Brüchen entstehende kleinste gemeinsame Nenner.Bevor du den Hauptnenner bildest, kürzt du die Brüche so weit wie möglich.
Der Hauptnenner ist das kleinste gemeinsame Vielfache (kgV) der Nenner.
Erweitere
und
auf ihren Hauptnenner.
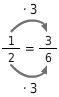
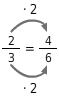
Hauptnenner
Vielfache von 2: {
,
,
,
, ...}
Vielfache von 3: {
,
,
,
, ...}
Das kleinste gemeinsame Vielfache von 2 und 3 ist 6. Du erweiterst
und
auf ihren Hauptnenner
.


Erweitere
und
auf ihren Hauptnenner.
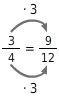
Hauptnenner
Vielfache von 4: {
,
,
,
, ...}
Vielfache von 6: {
,
,
, ...}
Das kleinste gemeinsame Vielfache von 4 und 6 ist 12. Du erweiterst
und
auf ihren Hauptnenner
.



