Adaptive Hausaufgaben und Übungen
Aufgaben für die Jahrgangsstufen 4 bis 12/13
Personalisierte Rückmeldungen und Hilfestellungen
Automatische Korrektur jeder Eingabe
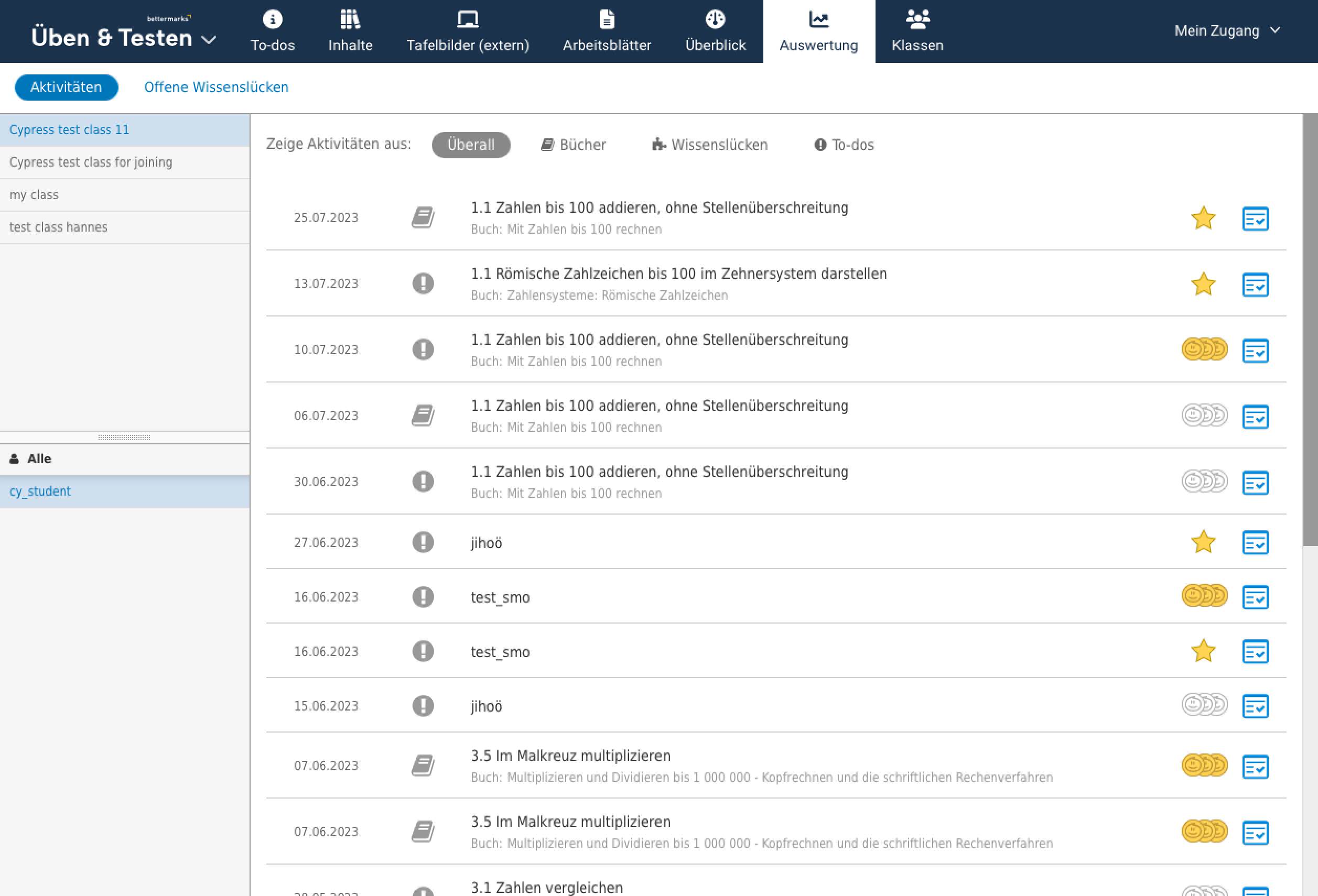
Übersichtliche Auswertung zum Lernstand der Klasse

»Üben & Testen« bietet adaptive Aufgaben. Schülerinnen und Schüler bekommen verstehensorientierte Rückmeldungen und Sie erhalten übersichtliche Auswertungen.
2.300 Übungen mit über 200.000 Aufgaben zum differenzierten Arbeiten am Computer, Laptop oder Tablet: für Hausaufgaben oder Übungsphasen im Unterricht.
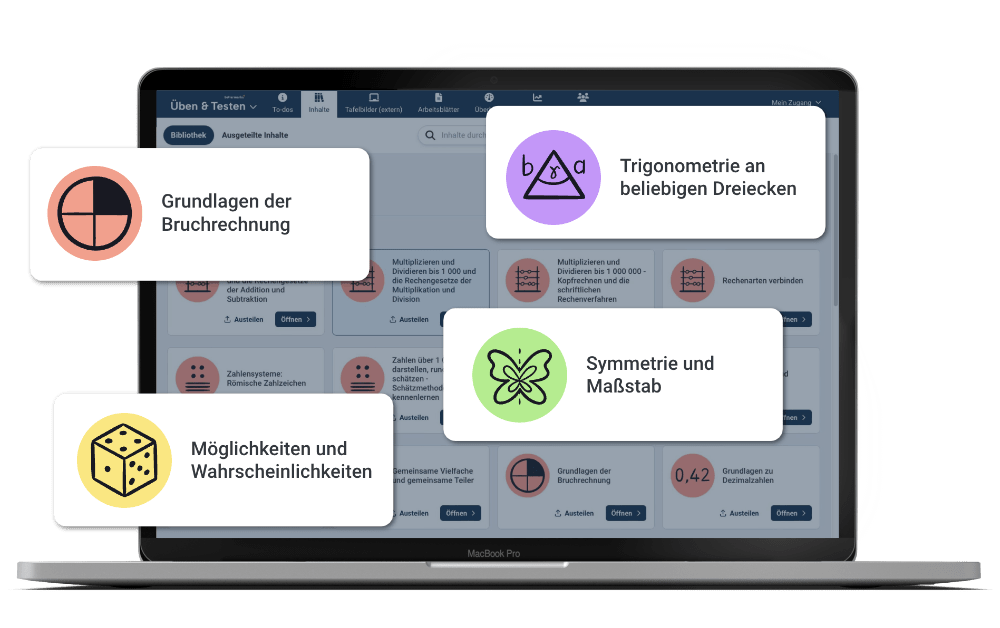
Teilen Sie die Übungen und Tests an die ganze Klasse oder individuell aus. Alle Aufgaben sind parametrisiert, sodass Ihren Schülerinnen und Schülern das Übungsmaterial nie ausgeht.
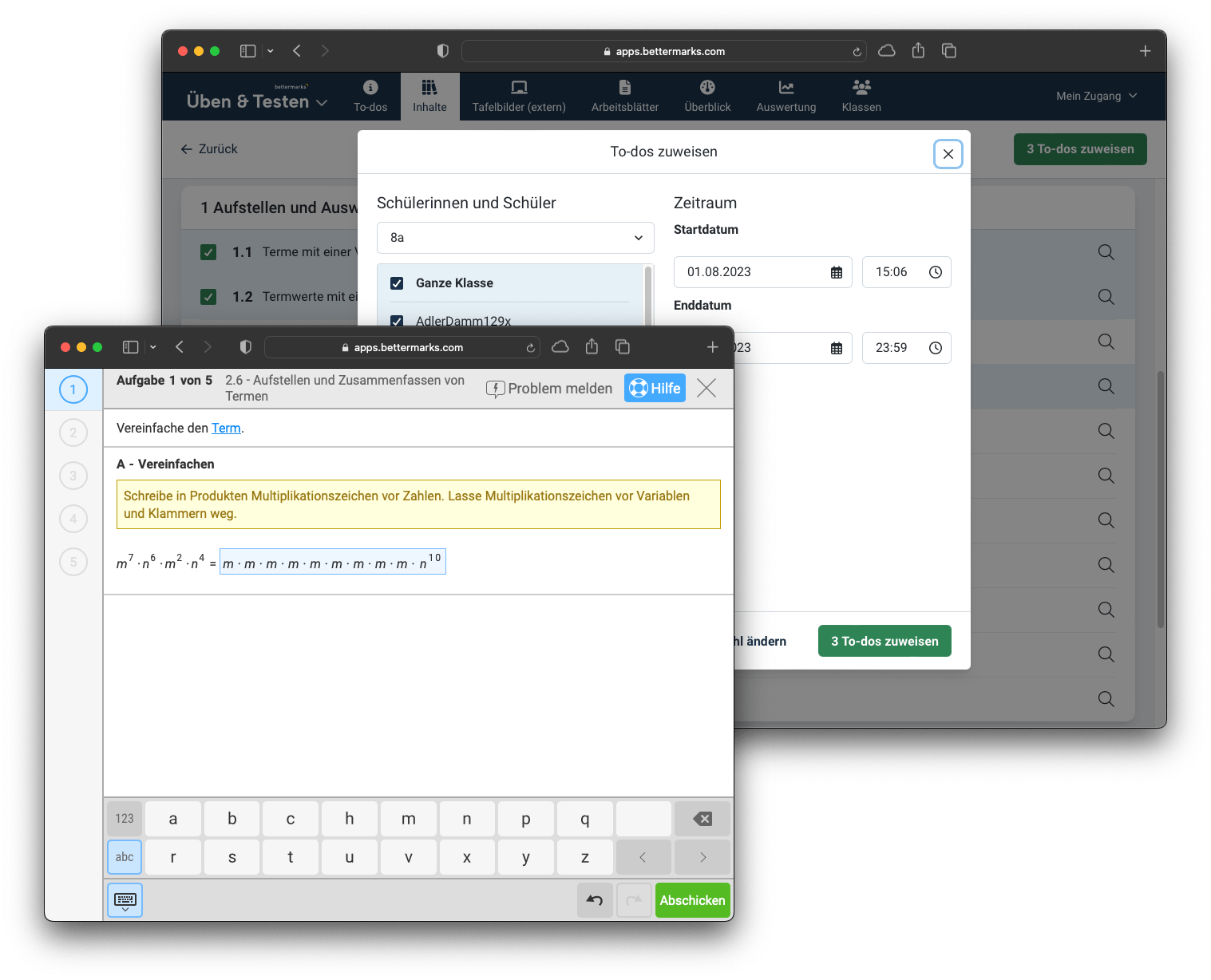
Alle Aufgaben werden automatisch korrigiert und ausgewertet. Sie überblicken den Lernstand und werden auf erkannte Fehlvorstellungen hingewiesen, sodass Sie genau wissen, was wiederholt werden sollte.

bettermarks das führende Intelligentes Tutortielle System (ITS) für das Fach Mathematik und bildet die drei Eigenschaften für die höchste Lernwirksamkeit ab.

2.300 Übungen mit über 200.000 Aufgaben zum differenzierten Arbeiten am Computer, Laptop oder Tablet: für Hausaufgaben oder Übungsphasen im Unterricht.

Praesent commodo cursus magna, vel scelerisque nisl consectetur et.
Sed posuere consectetur est at lobortis. Aenean eu leo quam. Pellentesque ornare sem lacinia quam venenatis vestibulum. Donec sed odio dui. Donec ullamcorper nulla non metus auctor fringilla.
Sed posuere consectetur est at lobortis. Aenean eu leo quam. Pellentesque ornare sem lacinia quam venenatis vestibulum. Donec sed odio dui. Donec ullamcorper nulla non metus auctor fringilla.
Hier finden Sie Antworten zu den häufigsten Fragen. Anleitungen finden Sie im Hilfebereich.
Das »alte« bettermarks heißt nun »Üben & Testen« und hat einen neuen Anstrich bekommen. Gleichzeitig wird der Funktionsumfang erweitert und kontinuierlich verbessert.
»Üben & Testen« bietet ergänzende Übungs- und Testaufgaben zu Ihren bisherigen Unterrichtsmaterialien. In »Unterrichten« finden Sie Vorschläge für Unterrichtseinheiten mit Inhalten zu allen Phasen des Unterrichts.
Es gibt mehrere Bundesländer, die direkt mit bettermarks zusammenarbeiten. In diesen Bundesländern ist die Nutzung von bettermarks kostenfrei – teilweise unter bestimmten Voraussetzungen (zum Beispiel, wenn bettermarks über ein bestimmtes Lern-Management-System oder eine Bildungscloud genutzt wird).
Das ist leider nicht möglich: Eine Registrierung ist bei bettermarks nur für Lehrkräfte und Personen im Referendariat erlaubt, da immer die Zuordnung an eine Schule erfolgen und diese aus Datenschutzgründen offiziell bestätigt werden muss.
Im Hilfebereich finden Sie Anleitungen und Tipps zur Nutzung von bettermarks.