Potenzen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenDie n-te Potenz

Für eine reelle Zahl a und eine natürliche Zahl
ist:
Sprich: a hoch n
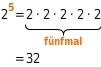
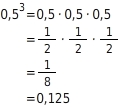
Potenzen mit negativer Basis
Das Produkt aus einer geraden Anzahl negativer Faktoren ist positiv. Damit ist auch eine Potenz mit negativer Basis und geradem Exponenten positiv.

Das Produkt aus einer
Anzahl negativer Faktoren ist negativ. Damit ist auch eine Potenz mit negativer Basis und
Exponenten negativ.
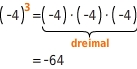
Steht vor der Potenz ein negatives Vorzeichen, bildest du die Gegenzahl.Du berechnest also die Potenz zunächst ohne das Vorzeichen zu beachten und änderst anschließend das Vorzeichen.


Basis oder Exponent einer Potenz bestimmen
Um eine Zahl als Potenz mit gegebener Basis darzustellen, schreibst du die Potenz als Produkt, in dem nur die Basis jeweils als Faktor vorkommt. Die Anzahl der Faktoren gibt den Exponenten an.
Die Basis 4 kommt dreimal als Faktor im Produkt vor, also ist:
Um eine Zahl als Potenz mit gegebenem Exponenten darzustellen, schreibst du die Potenz als Produkt gleicher Faktoren. Deren Anzahl entspricht dem Exponenten. Der Faktor gibt die Basis an.
Die Zahl 8 schreibst du als Produkt gleicher Faktoren:

