Rechnen für Fortgeschrittene
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du Rechenausdrücke mit mehreren Rechenoperatoren (+ , - , •, : ) und Klammern berechnest und wie du geschickt im Zahlbereich der rationalen Zahlen rechnen kannst.
- Punktrechnung vor Strichrechnung
- Klammerrechnung vor Punktrechnung vor Strichrechnung
- Innere Klammer vor äußerer Klammer
- Doppelbrüche auflösen
- Rechenvorteile nutzen mit dem Distributivgesetz
- Rechenvorschriften in eine Aufgabe umwandeln
- Welche Rechenoperation lässt sich in welchem Zahlbereich ausführen?
Punktrechnung vor Strichrechnung
Damit so etwas in der Mathematik nicht vorkommt, gibt es Rechenregeln, die zu einem eindeutigen Ergebnis führen. Hier gilt die Merkregel:
„Punktrechnung vor Strichrechnung“
Also rechnest du:
Klammerrechnung vor Punktrechnung vor Strichrechnung
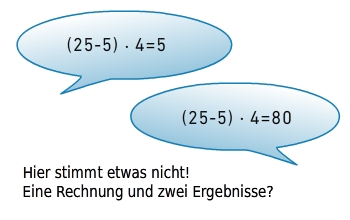Wenn eine Teilaufgabe in Klammern gesetzt ist, berechnest du zuerst das Ergebnis in der Klammer. Anschließend nutzt du dieses Ergebnis für die weiteren Berechnungen. Hier gilt die Merkregel:
„Klammerrechnung vor Punktrechnung vor Strichrechnung“
Also rechnest du:
Innere Klammer vor äußerer Klammer
Sind in der Aufgabe mehrere Klammern ineinander verschachtelt, berechnest du zuerst den Wert der inneren Klammer. Anschließend nutzt du dieses Ergebnis für die Berechnung der äußeren Klammern.Hier gilt die Merkregel:
„innere Klammer vor äußerer Klammer“
Also rechnest du:
Doppelbrüche auflösen
Bei einem Doppelbruch fasst du zuerst Zähler und Nenner so weit wie möglich zusammen. Ein Bruchstrich hat die gleiche Bedeutung wie ein Divisionszeichen. Statt als Doppelbruch, kannst du die Aufgabe auch als Divisionsaufgabe schreiben.
„innere Klammer vor äußerer Klammer“
So kannst du die Aufgabe aus der Sprechblase lösen:
Rechenvorteile nutzen mit dem Distributivgesetz
Manchmal kannst du eine Aufgabe leichter lösen, wenn du das Distributivgesetz (Verteilungsgesetz) nutzt. Das Distributivgesetz gestattet es, aus einer Summe oder einer Differenz einen gemeinsamen Faktor auszuklammern.
In der Summe
-8
ist der gemeinsame Faktor die
, denn sie kommt in beiden Produkten vor.
Zum Vergleich ohne Ausklammern:
Die Multiplikationsaufgaben sind hier anspruchsvoller als im ersten Beispiel.
Wenn du den gemeinsamen Faktor ausklammerst, brauchst du also weniger und einfachere Rechenoperationen auszuführen. Das ist besonders hilfreich bei langen Aufgaben und bei Aufgaben, in denen sich die Summanden günstig ergänzen.
Hier ist der gemeinsame Faktor die
, denn sie kommt in allen drei Produkten vor.
Rechenvorschriften in eine Aufgabe umwandeln
Um eine Rechenvorschrift wie „Addiere das Produkt von 4 und -11 zum Quotienten von -48 und 8“ in eine Rechenaufgabe umzuwandeln, gehst du schrittweise vor.
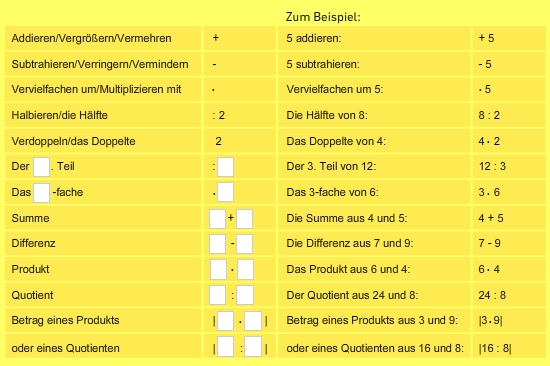
Wenn möglich, kannst du jetzt noch Vorzeichen und Rechenzeichen miteinander „verrechnen“. Hier gelten folgende Regeln:„+ und + ergibt +“„+ und - ergibt -“ „- und + ergibt -“ „- und - ergibt +“
Diese „übersetzungshilfen“ können dir die Umwandlung erleichtern:
Wenn möglich, kannst du jetzt noch Vorzeichen und Rechenzeichen miteinander „verrechnen“. Hier gelten folgende Regeln:„+ und + ergibt +“„+ und - ergibt -“ „- und + ergibt -“ „- und - ergibt +“
Diese „übersetzungshilfen“ können dir die Umwandlung erleichtern:
Welche Rechenoperation lässt sich in welchem Zahlbereich ausführen?
„Ausführbar“ ist eine Rechenoperation (wie +,-,•,:) immer dann in einem Zahlbereich, wenn alle Zahlen der Aufgabe und das Ergebnis der Aufgabe zu diesem Zahlbereich gehören.
In den natürlichen Zahlen mit der Null ℕ 0 sind die Addition und die Multiplikation immer ausführbar. Denn wenn du zwei natürliche Zahlen addierst oder multiplizierst, erhältst du immer eine natürliche Zahl
Subtrahierst oder dividierst du zwei natürliche Zahlen, zum Beispiel
oder
, dann erhältst du nicht immer eine natürliche Zahl.
In den ganzen Zahlen (
) sind die Addition, die Subtraktion und die Multiplikation immer ausführbar. Denn wenn du zwei ganze Zahlen addierst, subtrahierst oder multiplizierst, erhältst du immer eine ganze Zahl.
Dividierst du zwei ganze Zahlen, zum Beispiel
-3 , dann erhältst du nicht immer eine ganze Zahl.
In den rationalen Zahlen (
) sind die Addition, die Subtraktion, die Multiplikation und die Division immer ausführbar (ausgenommen ist die Division durch 0). Denn wenn du zwei rationale Zahlen addierst, subtrahierst, multiplizierst oder dividierst, erhältst du immer eine rationale Zahl.
