Rationale Zahlen kennenlernen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie die Menge der rationalen Zahlen aufgebaut ist und welche Eigenschaften die rationalen Zahlen besitzen.
Die Menge der rationalen Zahlen
Du kennst bereits die ganzen Zahlen (
). Sie lassen sich auf der Zahlengeraden darstellen:
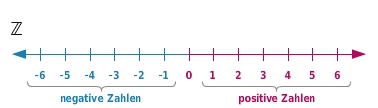Die Menge der rationalen Zahlen (
) erhältst du, wenn du alle positiven und negativen Bruchzahlen einschließlich der Null zusammennimmst.
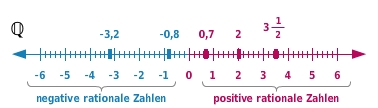Auch Dezimalzahlen wie
,
oder
gehören zu den rationalen Zahlen, denn sie lassen sich auch als Bruch darstellen.
Die Menge der rationalen Zahlen (
) erhältst du, wenn du alle positiven und negativen Bruchzahlen einschließlich der Null zusammennimmst.
Auch Dezimalzahlen wie
,
oder
gehören zu den rationalen Zahlen, denn sie lassen sich auch als Bruch darstellen.
Rationale Zahlen an der Zahlengeraden
Für die Menge der rationalen Zahlen muss die Einteilung der Zahlengeraden verfeinert werden. Welche Einteilung du wählst (z.B. Zehntel, Hundertstel, Tausendstel, Bruchteile, ...) hängt davon ab, welche Zahl du eintragen oder ablesen möchtest.
Um
an der Zahlengeraden anzugeben, brauchst du mindestens eine Zehnteleinteilung, da die letzte Nachkommastelle von -5,8 die 8 Zehntel sind.
Um
an der Zahlengeraden anzugeben, brauchst du mindestens eine Tausendsteleinteilung, da die letzte Nachkommastelle von
die 4 Tausendstel sind.
Um
an der Zahlengeraden anzugeben, muss der Bereich zwischen den ganzen Zahlen mindestens in drei Abschnitte (oder Teilabschnitte davon) unterteilt sein, da dies im Nenner des Bruchs vorgegeben ist.
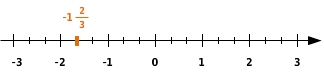
Je weiter links eine rationale Zahl auf der Zahlengeraden liegt, desto kleiner ist sie!
ist also kleiner als
ist also größer als
Betrag und Gegenzahl
Der Betrag einer Zahl ist der Abstand dieser Zahl zur Null.
hat den Abstand
zur Null, man schreibt: |
| =
(„der Betrag von
ist
“).
hat den Abstand
zur Null, man schreibt: |-1,3| = 1,3 („der Betrag von
ist
“).
Es gibt jeweils zwei Zahlen, die den gleichen Abstand zur Null und damit auch den gleichen Betrag haben. Jede dieser beiden Zahlen ist die Gegenzahl der anderen.
Die Gegenzahl zu
ist die
und umgekehrt.
